Premio Abel 2006: La fuerza de un analista

2006/07/01 Duoandikoetxea Zuazo, Javier - EHUko matematika irakaslea Iturria: Elhuyar aldizkaria

• Matematika

En 1902 aparecen tres intenciones de Niels Henri para conmemorar el primer centenario del nacimiento de Abel y difundir su prestigio: celebrar actos culturales, establecer una estatua y organizar un premio internacional. Se celebraron actos culturales, el Estado se inauguró en 1908, pero el premio no se organizó. Parece que estuvieron a punto de hacerlo, pero cuando en 1905 Noruega se separó de Suecia, allí fueron los sueños de crear el premio.

A punto de cumplirse el segundo centenario, se recuperó la idea centenaria y se pidió al gobierno noruego que creara un premio. En 2002 el gobierno noruego aprobó los estatutos del Fondo Abel. El objetivo principal del fondo es "Otorgar un premio internacional a un trabajo científico relevante en el campo de las matemáticas". Parece que este premio puede estar en el camino de ser un sustituto de lo que podría ser el Nobel de Matemáticas: dónde se emite --Noruego--, quién --los reyes noruegos o reina de Noruega -, cuánto dinero -casi, entre otros -. El futuro dirá si es así o no, según vayan cumpliendo los años.

Lennart Carlos

El premio Abel 2006 ha sido para Lennart Carles, matemático destacado en el análisis clásico. Nacido en Estocolmo en 1928, estudió en la Universidad de Uppsala, donde presentó su tesis doctoral en 1950. Las matemáticas, sobre todo el análisis, han tenido una gran tradición en Suecia, XIX. A partir de la segunda mitad del siglo XX. El propio director de Carleson, Arne Beurling, es un destacado analista.

Con 25 años consiguió el puesto de profesor de la Universidad de Estocolmo, pero pronto regresó a Uppsala. Allí fue profesor hasta 1993; años después, sin dejar de trabajar, fue también profesor de la Universidad UCLA de Los Ángeles.

Entre los trabajos de Carleson destacan la respuesta que ha dado a problemas difíciles que han estado pendientes de resolución durante varios años. Por ejemplo, en 1962 demostró el teorema de la Corona y, así, el matemático japonés Kakutani resolvió la pregunta que había lanzado veinte años antes.

Fue mayor lo que hizo cuatro años después, al resolver el mayor problema abierto de la teoría de series de Fourie, la convergencia punto a punto. Con ello entró en la historia de las Matemáticas.

Además, en la década de los 80, frente a la creencia de que los matemáticos obtienen sus principales resultados a edades tempranas, dio respuesta a un problema abierto en sistemas dinámicos suaves, junto a Michael Benedicks.

Además de todo esto, es evidente el trabajo de Carlesón por las Matemáticas. He aquí un ejemplo. En 1916 el matrimonio Mittag-Leffler declaró su intención de dejar su casa y su biblioteca a la Academia Sueca de Ciencias para crear un instituto de matemáticas. En 1927 murió Mittag-Leffler, el instituto se fundó, pero no se organizó por falta de dinero según sus intenciones. En 1967 el Gobierno sueco dio la oportunidad a Carleson de trabajar donde quería y él decidió poner en marcha el instituto Mittag-Leffler. También lo hizo, obtuvo las subvenciones necesarias y lo convirtió en uno de los centros de investigación más prestigiosos del mundo. Hasta 1984 fue director del instituto.

Series Fourie

Las series de Fourie están a punto de cumplir los doscientos años. De hecho, es de 1807 cuando Joseph Fourier presentó su primer trabajo a la Academia de la Ciencia de París. Propuso y resolvió la ecuación de la propagación del calor, inventando para ello una vía específica, la distribución de variables que ha resultado tan útil. La función que da la temperatura inicial se escribe como serie de seno y coseno, es decir, como suma infinita, y Fourier afirmó que esto es posible para todas las funciones.

Confirmar sí, probar no. No es de extrañar que hasta entonces desarrolló enormemente los análisis matemáticos

herramientas de cálculo, pero no “medios de prueba geométricos”, en palabras de Cauchy. Como el nuevo viento del rigor requería pruebas, la afirmación de Fourie no era un teorema, pero se convirtió en un problema. Y muy importante, el XIX. En la génesis y evolución de muchos de los conceptos del análisis matemático del siglo XX fueron series trigonométricas: función, integral, convergencia uniforme...

XIX. La teoría clásica de las series de Fourie acababa con el siglo XIX. XX. En los primeros años del siglo XX, sin embargo, el sector fue completamente renovado. Las razones fueron dos: Teoría de la medida e integral de Lebesgue y teoría de los espacios funcionales, es decir, análisis funcional actual.

El aiero de Lusin llegó en 1913: si el cuadrado de una función es integrable, su serie de Fourie coincide en todos los puntos, excepto en un “conjunto de longitud cero”. La afirmación se debe al matemático ruso Lusin, no probada, pero sí con la convicción de ser un teorema.

Con el paso de los años se reunieron otros teoremas en el campo de las series de Fourie, pero nadie daba esa categoría a la conjetura de Lusin. Ni al contrario, porque eso también podía ocurrir. La verdad es que, a partir de un momento, entre los expertos empezó a generalizarse esa convicción de que la intuición de Lusin estuvo equivocada. Por eso, cuando en 1965 Carleson demostró el teorema, fue en cierta medida una sorpresa.

Él mismo ha contado que durante varios años intentó demostrar lo contrario. Cuando pensaba que tenía todas las herramientas disponibles para un contraposición, le resultó imposible. Entonces vio que tenía que tomar la otra vía, la de sí, y pudo conseguir el resultado con las herramientas acumuladas.

La prueba de Carleson tuvo desde el principio la fama de ser misterioso. Aunque técnicamente era correcto, no se entendía. Todavía parece que las causas de su estructura interna son demasiado inclinadas para la mayoría. Para utilizar la comparación del matemático Michael Christ es como la ascensión de un monte de ocho mil metros, la mayoría no somos capaces de caminar por nuestra cuenta, pero Carlesón nos demostró que hay un camino que lleva a la cima.

Sistemas dinámicos

También en otro campo de las matemáticas, Carleson hizo caminos a la cima, por ejemplo, en sistemas dinámicos.

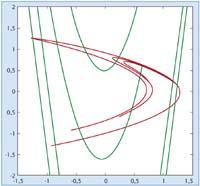
Tomar una función del plano al plano, por ejemplo, y aplicar la función varias veces comenzando en un punto. ¿Cuál es el comportamiento de la sucesión de puntos obtenida --orbital -? ¿Se acerca a un límite, va al infinito o hace algo más? A partir de esta pregunta y dependiendo de las funciones, surgió un campo de las Matemáticas. A finales del siglo XX, sobre todo de la mano del matemático francés Henri Poincaré.

Tras unos resultados teóricos, la verdadera innovación en el campo se produjo en el ordenador. Haciendo ver las órbitas de los puntos en la pantalla se podía sospechar de lo que podía pasar, para hacer conjeturas. Luego tendrían que venir las pruebas. De ahí surgió lo que han llamado la teoría del Caos.

Es frecuente citar un estudio del meteorólogo Lorentz como uno de los primeros ejemplos del caos. En 1976 otro meteorólogo, Michel Hénon, resumiendo las ecuaciones de Lorentz, dio un sistema de plano en el que aparece un comportamiento bastante particular. Se detecta un conjunto 'raro', en el que las órbitas se dirigen hacia allí (se aproximan al conjunto pero no a un valor concreto), pero si comenzamos en un punto del conjunto se obtiene una órbita que se desplaza en el mismo. Y no sólo eso, la estructura del conjunto es rara, ya que es fractal. Por eso se inventó el término "extraña atracción". ¿Es posible demostrarlo matemáticamente?

En la década de los 80 entró en Carles en el campo de los sistemas dinámicos. Junto a Michael Benedicks, inventó un nuevo método para estudiar un primer caso sencillo. Posteriormente, adaptaron el método para poder aplicarlo al sistema de Hénon y fueron capaces de describir su dinámica, convirtiendo la conjetura de años anteriores en un teorema. Con estos resultados, el artículo publicado por Carlos y Benedicks en 1992 ha quedado como un hito en la teoría de los sistemas dinámicos.