Regulamento de uso do abaco chinés (II). División

1991/02/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

No chinés bako ocuparémonos das regras paira realizar a división e no seguinte as raíces cadradas e cúbicas.

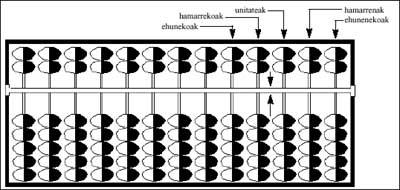
Elhuyar. No número 43 “Ciencia e Técnica”, no ábaco chinés demos todas as instrucións paira sumar, restar e multiplicar. Nesta ocasión, ocuparémonos das normas paira realizar a división no ábaco chinés e das que se necesitan paira obter as raíces cadradas e cúbicas.

División simple

É o caso de que o divisor sexa menor de 10 e non se utilizará o produto. Utilizaremos as seguintes palabras:

adiantar - subir as bólas na
columna da esquerda

Normativa

Parte:
una parte, adiantar 1; dous partes, adiantar 2; ... ; nove partes, adiantar 9.

Dous partes:
una por dous na mesma columna 5 (substituír 1a por 5); dous por dous, 1 adiantado; tres por dous (3 = 2+1), 1 adiantado (2/2), dous por tres e (1/2) na mesma columna 5; catro por dous, 2 adiantados; ...; nove por dous (9 = 8+1), 4 adiantados, 8 por nove e (1/2) na mesma columna.

Dividido por tres:una
entre tres na mesma columna, 3 máis 1; dous partes na mesma columna, 6 máis dúas; tres partes tres, 1 adiantadas; catro partes (4 = 3 + 1), 1 adiantada (3/3), 3 na mesma columna, máis 1 (1/3); ...

Parte catro:una
dividida por catro, 2 na mesma columna, máis 2; dúas partes planas, 5 na mesma columna; tres partes catro, 7 na mesma columna, máis 2; catro partes catro, 1 adiantado;...; nove partes catro (9 = 8 + 1), 2 adiantadas (4/8), 2 na mesma columna, máis 2 (1/4).

Parte cinco:una por cinco,
2 na mesma columna; dous por cinco, 4 na mesma columna; tres por cinco, 6 na mesma columna; catro por cinco, 8 na mesma columna; cinco por cinco, 1 adiantado; ...; nove por cinco (9 = 5+4), 1 adiantado (5/5), 8 na mesma columna (4/5).

Dividir seis:una por seis,
1 na mesma columna, máis 4; dous partes seis na mesma columna, máis 2; tres partes na mesma columna, seis na mesma columna; catro partes seis na mesma columna, 6 na mesma columna, máis 4; cinco partes seis na mesma columna, 2; seis partes seis, 1 adiantadas; ...; nove partes seis (9 = 6+3), 1 adiantada na mesma columna 5.

Parte sete:una por sete,
1 na mesma columna, máis 3; dous por sete, 2 na mesma columna, máis 6; tres partes por sete, 4 na mesma columna, 2; catro partes por sete, 5 na mesma columna, máis 5; cinco partes por sete, 7 na mesma columna, máis 1; seis partes pola mesma columna, 8 por 4; sete partes por sete, 1;...; nove partes por sete (9=7+2), 2), adiantados na mesma columna, 1, 2.

Parte oito:una por oito, na mesma columna 1, máis 2;
dous por oito, na mesma columna 2, máis 4; tres por oito, na mesma columna 3; catro por oito, na mesma columna 5; cinco por oito, na mesma columna 6, máis 2; seis por oito, na mesma columna 7, máis 4; sete por oito, na mesma columna 8, máis 6; oito partes oito, 1 avanzada; nove partes (9=8+1).

Parte nove:una
entre nove, 1 na mesma columna, máis 1; dous partes nove, 2 na mesma columna, máis 2; tres partes nove, 3 na mesma columna, máis 3; ...; oito partes nove, 8 na mesma columna, máis 8; nove partes nove adiantadas.

Observacións

Nota 1: Si na columna da dereita a bóla sobe máis de 9, non se pode subir esa décima na columna da esquerda. Deberá dividirse de memoria.

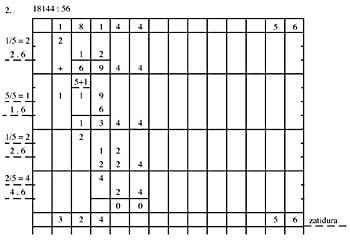
Ao dividir o dividendo sitúase á esquerda deixando una columna libre. O divisor colocarase á dereita.

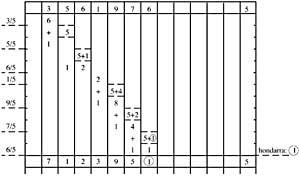
4/9{ 4 na mesma columna, máis 4 na columna dereita, 9+4
= 13;13/9 = 9+4, (9+3)/9, 1 adiantado na mesma columna 4; 4/9 na mesma columna, máis
4 na columna dereita, 8+4
= 12;12/9 na columna 12 = 9+3, (9+4)/9; 3 na mesma columna; 3/9, máis
3

9/9 avance

Nota 2: Se una vez dividida a última cifra, o cociente non é exacto, a area quedará na súa columna dereita (columna de unidades do dividendo).

Exercicios:

123456789 : 4 :5 ; 6 ; :7 ; :8 ; :9 ; 3936 : 4 ; 998651 : 7 ; 519256 : 8 ; 125476 : 2

División longa

É o caso no que o divisor é maior de 10.

Esta operación combina división simple, multiplicación e resta. Como antes empezamos pola esquerda.

Regra xeral:

dividir a primeira cifra do dividendo pola primeira do divisor.

Situar o cociente parcial na columna correspondente e multiplicar polas seguintes cifras do divisor (una a unha) e restar os resultados (un a un) ás cifras do dividendo

nas columnas correspondentes.

Esta regra xeral ten un problema multiplicando un cociente parcial por unha cifra do divisor cando é superior á cifra do dividendo correspondente. Neste caso ao cociente parcial réstaselle 1, 2, ..., ata que o cociente parcial “novo” multiplicado pola cifra do divisor inferior á cifra do dividendo.

número insuficiente nas deducións, cando a cifra do dividendo sexa inferior ao produto da cifra do dividendo, do cociente parcial e do divisor.

non hai dereito a deducir si na supresión parcial non
temos dereito a deducir o cocimiento parcial das
bólas na columna dereita

Normativa

As seguintes regras débense engadir ás regras da división simple e utilízanse cando as primeiras cifras do dividendo e do divisor son iguais, tanto cando o minuendo é insuficiente como cando non hai dereito a dedución.

Una parte: non hai un desconto insuficiente	9 na mesma columna máis 11 quitadas máis 1
Dous partes: non hai fiscalmente deducible	9 na mesma columna máis 21 eliminados máis 2
Tres partes tres: non hai un desconto insuficiente	9 na mesma columna máis 31, máis 3
Catro partes planas: non hai cotas de dedución insuficientes	9 na mesma columna máis 41 eliminadas máis 4
Cinco partes cinco: non hai fiscalmente deducible	9 na mesma columna máis 51, máis 5
Seis partes seis:non hai fiscalmente deducible	9 na mesma columna máis 61, máis 6
Sete partes sete: non hai un desconto insuficiente	9 na mesma columna máis 71, máis 7
Oito anacos oito: non hai fiscalmente deducible	9 na mesma columna máis 81 eliminados máis 8
Nove partes nove: non hai un importe de dedución insuficiente	9 na mesma columna máis 91, máis 9

Exemplos

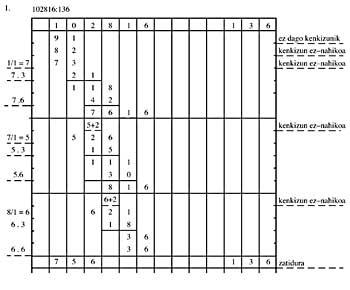
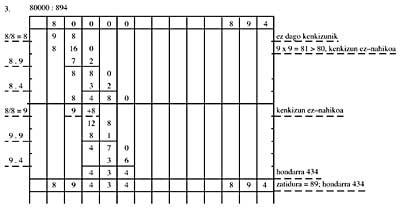
1. Exemplo: 102816 : 136

Se realizamos 1/1 = 1 quedariamos sen deducións paira poder eliminar 1.3 (00 - 1.3). Por tanto, segundo as normas, debemos escribir 9 na mesma columna e 1 na dereita.

Se realizamos 9/1 = 9, a diferenza que temos sería menor que 12, 9.3, é dicir, o minuendo non é suficiente. Por tanto, ao cociente 9 restaremos 1 e colocarémolo na columna da dereita.

Facendo 8/1 = 8 teriamos o problema anterior. Por tanto, ao cociente 8, quitamos 1 e colocámolo na columna da dereita.

7/1 = 7; 7.3 = 21. Como o minuendo agora é 32, 32 - 21 = 11

7.6 = 42, o minuendo agora é 118. Logo de 118 a 42 = 76.

Aquí a primeira división parcial

Facendo 7/1 = 7 ou 7/1 = 6, o minuendo sería demasiado pequeno paira poder eliminar 7.3 ou 6.3.

7/1 = 5; 5.3 = 15 o minuendo é 26, 26 - 15 = 11

5.6 = 30, deducible 111. Por tanto 111 - 30 = 81

8/1 = 6 por causas anteriores, xa que a dedución é insuficiente.

6.3 = 18, sendo o minuendo 21, 21 - 18 = 3

6.6 = 36, 36. Así, de 36 a 36 = 0. Cociente 756.

Observacións

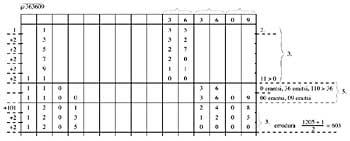
Aínda que en cada columna hai 7 (2/5) bólas, adóitanse indicar até 9 puntos. Si nalgúns cálculos intermedios hai que indicar máis de 9 puntos na mesma columna (16 no exemplo 3 no segundo paso e 12 no oitavo), pódense dar valores especiais ás bólas paira conseguir esa cantidade (10 no caso de 16 nas bólas superiores e 2 nas inferiores (16 = 1.10+3.2) no caso 12, 5 e 1, pero usando máis bólas (12 = 2.5 + 2.1).

Paira diferenciar o cociente das divisións do resto, ou da décima, hai que saber onde quedan as unidades do cociente: se o divisor ten una cifra, as unidades do cociente quedarán na primeira columna da esquerda das unidades do dividendo; se o divisor ten dúas cifras na segunda columna da esquerda das unidades, se ten tres na terceira columna; etc.

Exercicios:

1386 : 21; 6473 : 37 ; 749653 : 721 ; 563217 : 721 ; 150475 : 5122 ; 4820805 : 62413 : 344,40 : 28 ; 8383,20 : 65