Arkimedes-en behiak

Baina bere zaletasuna ez zen problema matematiko sakonei buruzkoa. Aitzitik, Arkimedesek matematikaren alderdi LUDIKOA ere landu zuen. Horren adibide gisa behien problema azalduko dugu.

Matematika klasikoak ebazpen zaileko problemak utzi zizkigun (zirkuluaren koadratura, angeluaren trisekzioa, Fermat-en teoremak, ...). Ideia berriekin edota arrazonamendu burutsuekin, horietako asko ebatzi dira, edo ebaztezinak direla frogatu da. Beste batzuek, aldiz, erantzun zain diraute. Harrigarria da horrenbeste problemen artean, Arkimedesen problemek kalkuluak besterik behar ez izatea. Kalkulu horiek egin ahal izateko 2.000 urte pasa behar izan dute. Hain kalkulu astunak ziren, ezen ordenadoreak baino ezin baitzien aurre egin.

K.a. III. mendean gaude, Arkimedesek zenbakiaren hurbilketa eman du:

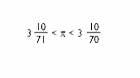
Apolonio Pergakoak hurbilketa hobea emateaz gain, zenbaki handien arteko biderkaketari buruzko tratatuan Arkimedesen lana ere kritikatu omen du. Arkimedesek, aurreko gertaerek zirikatuta, mendekua prestatu du; zenbaki handiak (bere lehiakideak menperatzen dituen horietakoak) behar dituen problema zail bat asmatu eta bidali baitio. Ez dakigu zer erantzun eman dion Apoloniok, baina problema bera Eratostenesi, Alexandriako liburuzainari, ere bidali dio eta horri esker ailegatu da gure eskuetara.
Guzti hori kondaira da eta ez dakigu egia den ala ez. Bestalde, problema, gutxienez, K.a. II. mendekoa dela eta ebazteko erabili behar diren zenbakiak benetan handiak direla ere onartzen da. Soluziorik txikienak, esate baterako, 206.545 zifra dauzka.

Problemaren enuntziatu osoa Gotthold Ephraim Lessing-ek aurkitu zuen 1773an Wolfenbüttel-go liburutegi batean. Grekoz idatzita zegoen eta lerro parekatuz osatua zen. Laburbildua honela gera daiteke:

Kalkula ezazu, laguna, Eguzkiko abere-kopurua. Buruz ekin iezaiozu horri, jakituriarik baldin baduzu. Kalkula ezazu behin batean Siziliako ordeketan alatzen zirenen kopurua, koloreen arabera lau taldetan banatuak: bat zuria, beste bat beltza, beste bat gorria eta pintoa azkena. Zezenak behiak baino gehiago ziren, ondoko baldintzetan:

1. Zezen zuriak = zezen gorriak + (1/2 + 1/3) zezen beltzak.
2. Zezen beltzak = zezen gorriak + (1/4 + 1/5) zezen pintoak.
3. Zezen pintoak = zezen gorriak + (1/6 + 1/7) zezen zuriak.
4. Behi zuriak = (1/3 + 1/4) saldo beltza.
5. Behi beltzak = (1/4 + 1/5) saldo pintoa.
6. Behi pintoak = (1/5 + 1/6) saldo gorria.
7. Behi gorriak = (1/6 + 1/7) saldo zuria.

Saldo bakoitzeko zezen eta behien kopuruak eman ahal badituzu, laguna, ez duzu zenbakien artea arerio. Baina, oraindik ezin zara jakintsuen taldean sartu. Horretarako Eguzkiko zezenen arteko ondoko erlazioak hartu beharko dituzu kontutan:

8. Zezen zuriak + zezen beltzak = karratu osoa (p2).
9. Zezen pintoak + zezen gorriak = zenbaki triangeluarra (n(n+1)/2).

Saldo osoa kalkulatzen duzunean, orduan, laguna, aldarrika ezazu garaile zure burua eskubide osoz, eta harro ibil zaitez zure izenak jakituriaren munduan distira egingo baitu.

Ikus daitekeenez, bi problema batean agertzen dira. Lehenengo zazpi baldintzak dituena ebazten erraza da. Bederatziak dituenak, ordea, zailtasunak sortu ditu 2.000 urtetan.

Kontutan hartu behar da biok infinitu soluzio onartzen dutela. Problema soluzio txikiena bilatzean datza. Eragiketa algebraikoak burutuz gero, ondoko emaitzak lortuko dira:

Zezen zuriak = 10 366 482 K
Zezen beltzak = 7 460 514 K
Zezen pintoak = 7 358 060 K
Zezen gorriak = 4 149 387 K

Behi zuriak = 7 206 360 K
Behi beltzak = 4 893 246 K
Behi pintoak = 3 515 820 K
Behi gorriak = 5 439 213 K

Aurreko emaitzetan K edozein zenbaki arrunt da. K-ri balioak emanez, soluzio desberdinak lortzen dira. Soluziorik txikiena K = 1 eginez lortzen da. Kasu horretan abereen kopuru osoa 50 389 082 da.

Bigarren problemari dagokionez, ez dirudi Arkimedesen garaian ebazteko erremintarik zegoenik. Izan ere, duela 100 urte arte ez zen aurrerapenik lortu. 1880. urtean A. Amthor alemaniarrak ekuazioak erabilgarriago bihurtu zituen eta soluzioa 776 ... hasten zela eta 206.542 zifra zituela esan zuen. Lehenengoan asmatu zuen, baina bigarrenean 3 zifraz oker zebilen.

Errorerik gabeko lehenengo soluzioa ordenadore baten bidez lortu zen 1965ean, baina ez zen inon argitaratu. Programaren egileak H.C. Willians, E.A. German eta C.R. Zarnke kanadarrak izan ziren. 1981ean Harry L. Nelson estatubatuarrak CRAY-1 ordenadorea probatzeko erabili zuen problema. 10 minututan lortu zuen soluzioa eta 47 orrialdetan inprimatu zuen. 47 orrialdeak “Journal of Recreational Mathematics” aldizkariaren 13. bolumeneko 3. alean daude.

Zergatik dira horren desberdinak lehenengo eta bigarren problemaren soluzioak? 8. baldintza betetzea ez da hain zaila. Zezen zuriak eta beltzak, guztira, 17 826 996 K dira. Beraz, K = 17 826 996 balioa hartuz karratu osoa lortuko dugu. Zailtasuna 9. baldintza kontutan hartzen denean sortzen da.

8. baldintza honela idatz dezakegu:

p ² = 17 826 996 K =
= 4 . 4 456 749 K;

orain, K = 4 456 749 t ² aukeratuz eta aurreko berdintzan ordezkatuz, honakoa lortzen da:

p ² = 4 . 4 456 749 . 4 456 749 t ² =
= 2 ² . (4 456 749)2 . t ² =
= (2 . 4 456 749 . t) ² ,

hau da, karratu osoa dugu. Hori da Amthor-ek lortu zuen aurrerapena. Hortaz, K = 4 456 749 t2 aukeratuz gero 9. baldintza honela idatz daiteke:

Zezen pintoak + zezen gorriak = 51 285 802 909 803 . t ² dela kontutan hartuz,

51 285 802 909 803 . t ² = n (n+1) / 2

n, t zenbaki arruntak izanik.

(Irakurleari aurreko berdintzaren soluzioa ez bilatzea gomendatzen diogu).

CRAY-1 probatzeko Arkimedesen problema erabili zutenak ez ziren gustora geratu lehenengo soluzioarekin eta hurrengo bostak bilatzeari ekin zioten. Bost horietako handienak milioi bat baino zifra gehiago du. Saldo ederra!

Gure galdera hauxe da: nola bizi zitekeen horrenbeste abere Sizilian?