Vacas de Arquímedes

1994/02/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

Pero su afición no se refería a problemas matemáticos profundos. Por el contrario, Arquímedes también abordó el aspecto LÚDICO de las matemáticas. Un ejemplo de ello es el problema de las vacas.

La matemática clásica nos dejó problemas de difícil resolución (cuadratura del círculo, trisección del ángulo, teoremas de Fermat, ...). Con nuevas ideas o razonamientos ingeniosos se han resuelto muchas de ellas o se ha demostrado que son insolubles. Otros, sin embargo, siguen esperando respuesta. Es sorprendente que entre tantos problemas, los problemas de Arquímedes sólo necesiten cálculos. Para poder hacer estos cálculos han tenido que pasar 2000 años. Eran cálculos tan pesados que sólo el ordenador podía resistir.

a.C. III. Estamos en el siglo XX, Arquímedes ha dado una aproximación al número:

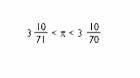
La Clave Apolonio, además de ofrecer una mejor aproximación, ha criticado el trabajo de Arquímedes en el tratado sobre la multiplicación de grandes números. Arquímedes, agobiado por hechos anteriores, prepara una venganza al inventar y enviar un difícil problema que necesita grandes números, de los que domina a sus competidores. Se desconoce la respuesta de Apolonio, pero también ha enviado el problema a Eratóstenes, el bibliotecario de Alejandría, y gracias a ello ha llegado a nuestras manos. Todo esto es leyenda y no sabemos si es cierto o no. Por otra parte, el problema es, al menos, el de C. II. También se admite que es un subordinado y que los números a utilizar para resolver son verdaderamente grandes. La solución más pequeña, por ejemplo, tiene 206.545 cifras.

El enunciado completo del problema fue descubierto en 1773 por Gotthold Ephraim Lessing en una biblioteca de Wolfenbüttel. Estaba escrito en griego y estaba formado por líneas pareadas. La resumida puede quedar como sigue:

Calcula, amigo, el número de reses solares. Piensa en ello si tienes conocimientos. Calcula una vez el número de personas que se alojaban en las llanuras sicilianas, divididas por colores en cuatro grupos: uno blanco, otro negro, otro rojo y el último pinto. Los toros eran más que vacas, en las siguientes condiciones:

1. Toros blancos = toros rojos + (1/2 + 1/3) toros negros. 2. Toros negros = toros rojos + (1/4 + 1/5) toros pintados. 3. Toros pintos = toros rojos + (1/6 + 1/7) toros blancos. 4º Vacas blancas = (1/3 + 1/4) saldo negro. 5. Vacas negras = (1/4 + 1/5) saldo pintado. 6º Vacas pintas = (1/5 + 1/6) saldo rojo. 7. Vacas rojas = (1/6 + 1/7) saldo blanco.

Si puedes donar el número de reses y vacas por cada saldo, amigo, no tienes rival entre los números. Pero todavía no puedes formar parte del grupo de sabios. Para ello deberá tener en cuenta las siguientes relaciones entre las reses solares:

8º. Toros blancos + toros negros = todo el cuadrado (p2). 9. Toros pintos + toros rojos = número triangular (n(n+1)/2).

Cuando calcules todo el saldo, entonces, amigo, apúntate de pleno derecho y presume de que tu nombre brilla en el mundo del conocimiento.

Como se puede observar, dos problemas aparecen en uno. Las siete primeras condiciones son fáciles de resolver. Sin embargo, los nueve han creado dificultades durante 2.000 años.

Hay que tener en cuenta que ambos aceptan infinitas soluciones. El problema consiste en buscar la solución más pequeña. La realización de operaciones algebraicas permitirá obtener los siguientes resultados:

Toros blancos = 10 366 482 K Toros negros = 7 460 514 K Toros pintos = 7 358 060 K Toros rojos = 4 149 387 K Vacas blancas = 7 206 360 K Vacas negras = 4 893 246 K Vacas pintas = 3 515 820 K Vacas rojas = 5 439 213 K

En los resultados anteriores K es cualquier número natural. Dando valores a K se obtienen diferentes soluciones. La solución más pequeña se obtiene haciendo K = 1. En este caso el número total de animales es de 50 389 082.

En cuanto al segundo problema, parece que en la época de Arquímedes no había herramientas para resolver. Y es que hasta hace 100 años no se consiguió ningún avance. En 1880 A. El alemán Amthor hizo más útiles las ecuaciones y dijo que la solución comenzaba por 776 ... y tenía 206.542 cifras. Acertó en la primera, pero en la segunda se equivocaba de 3 cifras.

La primera solución sin errores se obtuvo en 1965 mediante un ordenador, pero no se publicó en ningún sitio. Autores del programa H.C. Willians, S.A. German y C.R. Se trata de los zarnques canadienses. En 1981 Harry L. El norteamericano Nelson utilizó el problema para probar el ordenador CRAY-1. Obtuvo la solución en 10 minutos y la imprimió en 47 páginas. Las 47 páginas se encuentran en el número 3 del volumen 13 de la revista “Journal of Recreational Mathematics”.

¿Por qué las soluciones del primer y segundo problema son tan diferentes? Cumplir la condición 8 no es tan difícil. Los toros blancos y negros suman 17 826 996 K. Por lo tanto, tomando K = 17 826 996, obtenemos el cuadrado completo. La dificultad surge cuando se tiene en cuenta la condición 9.

La condición 8 puede escribirse como:

p 2 = 17 826 996 K = 4 . 4 456 749 K;

ahora, eligiendo K = 4 456 749 t 2 y sustituyéndolo en la igualdad anterior, se obtiene:

p 2 = 4 . 4 456 749 4 456 749 t 2 = 2 . (4 456 749)2 . t 2 = (2 . 4 456 749 t) 2 ,

es decir, tenemos todo el cuadrado. Ese es el progreso que consiguió Amthon. Así, si se selecciona K = 4 456 749 t2, la condición 9 se puede escribir como:

Toros pintos + toros rojos = 51 285 802 909 803 . teniendo en cuenta que t 2

51 285 802 909 803 t 2 = n (n+1) / 2

n, siendo t números naturales.

(Recomendamos al lector que no busque la solución de la igualdad anterior).

Los que utilizaron el problema de Arquímedes para probar el CRAY-1 no se quedaron a gusto con la primera solución y comenzaron a buscar las cinco siguientes. La mayor de estas cinco cifras supera el millón de euros. ¡Buen saldo!

Nuestra pregunta es ¿cómo se podía vivir tanto ganado en Sicilia?