Vacas de Arquímedes

1994/02/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

Pero a súa afección non se refería a problemas matemáticos profundos. Pola contra, Arquímedes tamén abordou o aspecto LÚDICO das matemáticas. Un exemplo diso é o problema das vacas.

A matemática clásica deixounos problemas de difícil resolución (cuadratura do círculo, trisección do ángulo, teoremas de Fermat, ...). Con novas ideas ou razoamentos enxeñosos resolvéronse moitas delas ou se demostrou que son insolubles. Outros, con todo, seguen esperando resposta. É sorprendente que entre tantos problemas, os problemas de Arquímedes só necesiten cálculos. Paira poder facer estes cálculos tiveron que pasar 2000 anos. Eran cálculos tan pesados que só o computador podía resistir.

a.C. III. Estamos no século XX, Arquímedes deu una aproximación ao número:

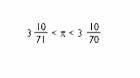
A Clave Apolonio, ademais de ofrecer una mellor aproximación, criticou o traballo de Arquímedes no tratado sobre a multiplicación de grandes números. Arquímedes, angustiado por feitos anteriores, prepara una vinganza ao inventar e enviar un difícil problema que necesita grandes números, dos que domina aos seus competidores. Descoñécese a resposta de Apolonio, pero tamén enviou o problema a Eratóstenes, o bibliotecario de Alexandría, e grazas a iso chegou ás nosas mans.
Todo isto é lenda e non sabemos si é certo ou non. Por outra banda, o problema é, polo menos, o de C. II. Tamén se admite que é un subordinado e que os números a utilizar paira resolver son verdadeiramente grandes. A solución máis pequena, por exemplo, ten 206.545 cifras.

O enunciado completo do problema foi descuberto en 1773 por Gotthold Ephraim Lessing nunha biblioteca de Wolfenbüttel. Estaba escrito en grego e estaba formado por liñas pareadas. A resumida pode quedar como segue:

Calcula, amigo, o número de reses solares. Pensa niso si tes coñecementos. Calcula una vez o número de persoas que se aloxaban nas chairas sicilianas, divididas por cores en catro grupos: un branco, outro negro, outro vermello e o último pinto. Os touros eran máis que vacas, nas seguintes condicións:

1. Touros brancos = touros vermellos + (1/2 + 1/3) touros negros.
2. Touros negros = touros vermellos + (1/4 + 1/5) touros pintados.
3. Touros pintos = touros vermellos + (1/6 + 1/7) touros brancos.
4º Vacas brancas = (1/3 + 1/4) saldo negro.
5. Vacas negras = (1/4 + 1/5) saldo pintado.
6º Vacas pintas = (1/5 + 1/6) saldo vermello.
7. Vacas vermellas = (1/6 + 1/7) saldo branco.

Se podes doar o número de reses e vacas por cada saldo, amigo, non tes rival entre os números. Pero aínda non podes formar parte do grupo de sabios. Paira iso deberá ter en conta as seguintes relacións entre as reses solares:

8º. Touros brancos + touros negros = todo o cadrado (p2).
9. Touros pintos + touros vermellos = número triangular (n(n+1)/2).

Cando calcules todo o saldo, entón, amigo, apúntache de pleno dereito e presume de que o teu nome brilla no mundo do coñecemento.

Como se pode observar, dous problemas aparecen nun. As sete primeiras condicións son fáciles de resolver. Con todo, o nove crearon dificultades durante 2.000 anos.

Hai que ter en conta que ambos aceptan infinitas solucións. O problema consiste en buscar a solución máis pequena. A realización de operacións algebraicas permitirá obter os seguintes resultados:

Touros brancos = 10 366 482 K Touros negros
= 7 460 514 K Touros pintos
= 7 358 060 K Touros vermellos
= 4 149 387 K Vacas brancas

= 7 206 360 K Vacas negras
= 4 893 246 K Vacas pintas
= 3 515 820 K Vacas vermellas
= 5 439 213 K

Nos resultados anteriores K é calquera número natural. Dando valores a K obtéñense diferentes solucións. A solución máis pequena obtense facendo K = 1. Neste caso o número total de animais é de 50 389 082.

En canto ao segundo problema, parece que na época de Arquímedes non había ferramentas paira resolver. E é que até fai 100 anos non se conseguiu ningún avance. En 1880 A. O alemán Amthor fixo máis útiles as ecuacións e dixo que a solución comezaba por 776 ... e tiña 206.542 cifras. Acertou na primeira, pero na segunda equivocábase de 3 cifras.

A primeira solución sen erros obtívose en 1965 mediante un computador, pero non se publicou en ningún sitio. Autores do programa H.C. Willians, S.A. German e C.R. Trátase dos zarnques canadenses. En 1981 Harry L. O norteamericano Nelson utilizou o problema paira probar o computador CRAY-1. Obtivo a solución en 10 minutos e imprimiuna en 47 páxinas. As 47 páxinas atópanse no número 3 do volume 13 da revista “Journal of Recreational Mathematics”.

Por que as solucións do primeiro e segundo problema son tan diferentes? Cumprir a condición 8 non é tan difícil. Os touros brancos e negros suman 17 826 996 K. Por tanto, tomando K = 17 826 996, obtemos o cadrado completo. A dificultade xorde cando se ten en conta a condición 9.

A condición 8 pode escribirse como:

p ² = 17 826 996 K
= 4 . 4 456 749 K;

agora, elixindo K = 4 456 749 t ² e substituíndoo na igualdade anterior, obtense:

p ² = 4 . 4 456 749 4 456 749 t ²
= ² . (4 456 749)2 . t ²
= (2 . 4 456 749 t) ² ,

é dicir, temos todo o cadrado. Ese é o progreso que conseguiu Amthon. Así, se se selecciona K = 4 456 749 t2, a condición 9 pódese escribir como:

Touros pintos + touros vermellos = 51 285 802 909 803 . tendo en conta que t ²

51 285 802 909 803 t ² = n (n+1) / 2

n, sendo t números naturais.

(Recomendamos ao lector que non busque a solución da igualdade anterior).

Os que utilizaron o problema de Arquímedes paira probar o CRAY-1 non quedaron a gusto coa primeira solución e comezaron a buscar o cinco seguintes. A maior destas cinco cifras supera o millón de euros. Bo saldo!

A nosa pregunta é como se podía vivir tanto gando en Sicilia?