"Crebacabezas"

1989/01/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

Desde os infantís de 6, 8,… pezas até os de 3.000-5.000 pezas paira persoas tranquilas existe una gran variedade e neste tipo de cabezudos a dificultade aumenta co número de pezas. Pero non son as que queremos traer aquí. Creemos que a dificultade non sempre está nos crebacabezas con moitas pezas. As que aparecerán aquí, ademais de ter poucas pezas, teralas que facer ti.

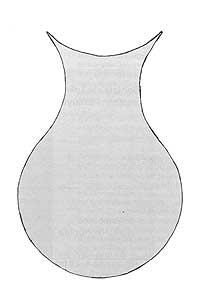
A primeira é a maceta e cadrada que tes aquí. Preguntarasche si estas dúas imaxes teñen algo que ver, sendo una redonda e outra cadrada. Aí está a clave, porque si divídense ben as dúas imaxes pódese converter una na outra. Aínda que esta división pódese realizar de diversas formas, neste caso a dificultade non radica na división multipieza, senón na división mínima de pezas posible.

Queremos traer a este tipo de persoas. Dous son o dodecágono e cadrado e a estrela e cadrada de seis vértices (Figuras 2 e 3). Aínda que pareza mentira, é posible asociar imaxes de formas tan diferentes mediante unha adecuada descomposición. Búscao ti. Por suposto, como no caso anterior, a descomposición débese tentar no menor número posible de pezas. Paira iso temos que dicir que as medidas das imaxes son precisas, é dicir, si a estrela divídese, por exemplo, o cadrado que hai que conseguir é o do seu lado. É dicir, son polígonos da mesma superficie.

Pero, onde está a orixe destes crebacabezas? Paira responder a esta pregunta debemos ir á historia.

a.C. No século V, os matemáticos eran atraídos por cuestións que hoxe coñecemos como “cuestións clásicas de xeometría”. Este tres cuestiones eran a trisección do ángulo, a duplicación do cubo e a cuadratura do círculo. Esta última é a que nos interesa.

Por que os matemáticos expuñan esta cuestión? Sen dúbida, a cuestión xurdiu cando o radio ou o diámetro obrigaban a calcular a superficie do círculo, e desde este punto de partida converteuse en cuestión geométricamente de equivalencia, dando o radio dun círculo paira calcular a diferenza do cadrado equivalente. Chegados a este punto, debemos dicir que naquela época non coñecían o valor exacto do número de \{ (pi). Por tanto, a resolución da cuestión non era tan sinxela como agora.

Pero imos ver como o conseguiron ao cadrado do círculo. Pitagórico VIN. Xa no século XX resolvera o cuadratura dos polígonos (estes son os nosos responsables). Con todo, ao pasar dos polígonos ao círculo as súas fórmulas e métodos eran inaplicables. Por tanto, os ensaios realizados sen medios especiais fracasaron.

En cambio, destacaron as sesións dos sofistas Antifon e Brison. A primeira, a partir da emisión dun Polígono inscrito, pódese obter outro de dobre número de lados baseado na propiedade e a medida que o número de lados aumenta, o polígono achégase ao círculo, ao ser todos os polígonos cuadrables deduciuse que o círculo tamén debería ser cuadrable. Una consecuencia falsa, como dixo Aristóteles: aínda que o número de lados é moi elevado, o polígono nunca cumprirá o círculo. Brison, pola súa banda, engadiu ao devandito razoamentos análogos aos dos polígonos circunscritos, mostrando que as dúas secuencias de polígonos abarcaban o círculo e que a superficie do círculo quedaba entre as superficies de dous polígonos, uno inscrito e outro circunscrito.

Leste foi o camiño que Arquímedes tomou paira pór fin a esta cuestión. Con todo, paira poder dar este último paso era necesario seguir dous máis. O primeiro deuno Hipias, a curva chamada cuadrador de Hipias. Definiuno no século V. O segundo foi o matemático Dinostrato, que a través do cuadrador de Hipias podía corrixirse a circunferencia. IV. Cando o demostrou no século XX. O último paso, como dixemos, deuno Arkimedes. III. Cando demostrou que no século XVIII podíase pasar dunha circunferencia dirixida a un cadro do círculo (mediante regra e compás). Os valores aproximados dados por Arquímedes paira obter isto paira o número \{ (pi) eran 3 10/71 = 4’1408… e 3 1/7 = 3’1428…

Como vimos, as cuadraturas dos polígonos axudaron a buscar a do círculo. Isto era precisamente o que nós queriamos traer aquí. E é que, como xa se mencionou anteriormente, con estas parellas de imaxes preténdese que tanto a maceta como a dodecágona ou a estrela teñan a mesma superficie que o cadrado que teñen ao seu lado, é dicir, mantendo a superficie estas figuras deben converterse en cadrados.

Se pedímosche descomposición coas imaxes anteriores, esta vez nós dámosche a descomposición dun cadrado e ti terás que buscar o cadrado (Figura 4). Este xogo consta de só cinco pezas, pero a súa dificultade supera a dalgúns puzzles de moitas pezas (medidas concretas).

Tamén hai persoas que se dedican a burlar, como o que me deu un alumno de informática. Chámase pony de Loyd e atópase aquí (Figura 5). Exponse:

“Con estas cinco pezas tes que formar a imaxe dun cabalo, na captura da forma máis aérea”.