Claude Shannon, pai do mundo dixital
2016/09/01 Leturia Azkarate, Igor - Informatikaria eta ikertzailea Iturria: Elhuyar aldizkaria

Preguntados polas persoas máis importantes do mundo das Tecnoloxías da Información e a Comunicación, a maioría da xente probablemente non será capaz de dar nomes máis aló de Bill Gates, Steve Jobs, etc. Os que coñecemos mellor o mundo da informática seguramente diriamos outros nomes como Alan Turing ou Tim Berners-Le. Entre nós quizais non tanto mencionarían a Claude Shannon. Non sabemos cal é a razón, pero Shannon non ten en absoluto a fama que merecen as súas inmensas achegas; Shannon, por exemplo, será o nome máis importante do mundo do TIC.
Claude Elwood naceu o 30 de abril de 1916 nunha aldeíña do estado norteamericano de Michigan. Desde a súa infancia ensinou na escola a competencia en ciencia e matemáticas, así como a afección pola invención e construción de dispositivos mecánicos e eléctricos. Así, en 1932, con tan só 16 anos, comeza os seus estudos universitarios na Universidade de Michigan, e en 1936 termina as súas carreiras de matemáticas e enxeñaría eléctrica. Posteriormente, en 1936, comezou a cursar un máster en enxeñaría eléctrica no prestixioso Massachusetts Institute of Technology ou MIT. E en 1940 defendeu a tese doutoral en matemáticas nesa mesma institución.
Fundamentos de Electrónica Dixital
Con todo, a primeira das súas dúas maiores achegas á ciencia realizouna antes da tese, concretamente no proxecto de máster, con tan só 21 anos. Segundo varios expertos, foi a tese de máster máis importante da historia.
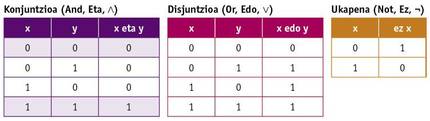
Durante a realización do máster, Shannon puido traballar cun dos computadores máis potentes da época, o analizador diferencial de Vannevar Bush. Aqueles computadores de entón eran analóxicos, funcionaban con poleas, engrenaxes, etc. e ocupaban un gran espazo. Tamén tivo a oportunidade de coñecer a álxebra de Boole nos seus estudos de matemáticas. Na álxebra de Boole as variables non teñen valor numérico senón Verdade e Mentira (ou 0 e 1), e as operacións básicas non son suma e multiplicación, senón conxunción, disyunción e negación (And, Or e Not). Estas operacións defínense mediante as seguintes táboas da verdade:
Shannon deseñou no proxecto do máster circuítos eléctricos de interruptores que implementaban a álxebra de Boole. Ademais, demostrou que as combinacións destes circuítos permitían realizar calquera operación matemática ou lóxica e deseñou algúns deles. Este traballo sentou as bases paira o deseño de circuítos dixitais e de aí xurdiu a electrónica dixital. O computador e todos os demais dispositivos electrónicos e dixitais viñeron grazas á visión que tivo no proxecto do seu máster.
Teoría da información, base do almacenamento de información e comunicación dixital
A pesar de que esta achega é realmente impresionante e sorprendente, considérase a súa achega máis importante. Shannon é sobre todo coñecido pola creación dun campo de coñecemento da teoría da información e polo seu desenvolvemento case completo, en 1948, cando traballaba en prestixiosos laboratorios Bell, escribiu no seu artigo “A mathematical theory of communication”.
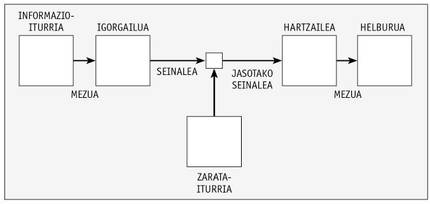
Neste artigo, Shannon definiu un sistema de comunicación a través da imaxe inferior.
Así, analiza e propón formas paira codificar a mensaxe da maneira máis adecuada. A imaxe pódese aplicar da mesma maneira a un sistema de almacenamento no que se escribe una información nun medio no que o sinal almacenado no mesmo pode sufrir una degradación e debe ser a mesma que a información escrita ao ler.
No artigo, Shannon propuxo converter a información en base binaria paira o almacenamento e transporte da información, é dicir, mediante os números 0 e 1. A estas unidades de información indicóuselles por primeira vez en devandito artigo binary digit ou bit, aínda que o nome fose J. W. Era a proposta de Tukey, compañeiro de Shannon.
Converter a información en dixital era un gran avance. De feito, a información analóxica que se utilizaba até o momento ten máis situacións posibles (infinitas en realidade), e dado que a diferenza dunha situación a outra é pequena, todo ruído ou pequeno cambio no almacenamento ou transmisión fai que una sinal convértase noutra e é imposible recuperar a información exacta orixinal. Isto ocasionaba grandes problemas na transmisión dos sinais, por exemplo, incluso levantando periodicamente a potencia do sinal con repetidores, xa que se producía una degradación e perda de información irreparable. Pola contra, trasladando a información á base binaria, só existen dúas situacións posibles, 0 e 1, e a diferenza entre ambas pode ser tan grande como se desexe no sinal físico (por exemplo, 0 voltios e 5 voltios). Así, aínda que o sinal degrádese ou modifica lixeiramente, é máis difícil converter un 0 nun 1 ou viceversa. Deste xeito, a información almacénase de forma máis sinxela e fiable, e a transmisión pódese realizar tan lonxe como se desexe mediante repetidores, sen perder información.
Isto, pola súa banda, supuña un gran avance, pero Shannon foi máis aló, definindo practicamente todas as técnicas e fórmulas matemáticas paira os métodos actuais de compresión e fiabilidade en almacenamento e comunicacións.
Paira iso definiu varios conceptos. Una delas é a información que emite unha mensaxe. De feito, Shannon dixo que non todas as mensaxes dan a mesma información: canto máis probable é unha mensaxe entre todos os posibles, menos información dá. Así mesmo, entre os símbolos ou caracteres dunha mensaxe, un símbolo máis frecuente facilita menos información. Paira medir a información dun símbolo deu a fórmula I = –log2 p, onde p é a probabilidade ou frecuencia do símbolo. Esta medida de información, ademais, indica o número de bits necesarios paira transmitir este símbolo. Así, necesitariamos un bit paira indicar cada un dos dous resultados (leon ou kastillo) que se poden obter ao lanzar una moeda, segundo a fórmula. Ou paira representar cada una das letras dun alfabeto de 27 letras, se todos tivesen a mesma probabilidade, serían necesarios 4,76 bits.
Tamén definiu a entropía dunha mensaxe. A entropía da mensaxe é a información media que contén unha mensaxe, polo que se define como: H =|Pi log2 pi. Ademais, dado que algúns dos símbolos son máis probables nuns contextos que noutros (no caso das letras, por exemplo, o habitual é que despois da q vaia a letra ou, ou que despois das consonantes é máis normal que una vogal que outra consonante), Shannon definiu tamén una entropía condicionada na que se ten en conta o signo anterior paira calcular as probabilidades. Pois ben, esta medida da entropía dinos até que punto unha mensaxe pódese comprimir sen perder información! Nas mensaxes de linguaxe natural, por exemplo, tendo en conta as frecuencias das letras e as frecuencias condicionadas, a entropía é menor que una, polo que cada letra pode codificarse en sinais de menos dun bit. E como o fixo Shannon. Os sistemas de compresión sen perdas (ZIP, RAR ou outros moitos que se utilizan nas comunicacións…) que tanto se utilizan na actualidade están baseados en fórmulas e métodos de Shannon.
Pouco con iso, Shannon teorizó tamén sobre a compresión con perda, e todos os sistemas que utilizan este tipo de compresión (JPG, MP3, DivX…) téñeno basicamente.
E aínda por riba, tamén escribiu nese artigo sobre códigos que detectan e/ou emendan erros. Paira detectar posibles erros ou emendar erros nunha información recibida ou lida envíase fundamentalmente información adicional redundante. Exemplo diso son os números de control nos números de conta ou letras que engadiron ao número do DNI español. Estas son, en definitiva, as sumas de checksum ou control. Se fallamos nalgún número, a suma de control non coincidirá e saberemos que hai un erro no número. Paira emendar o erro deberemos revisar manualmente xa que nestes exemplos só se utiliza o código paira detectar erros.
Pero existe a posibilidade de completar a mensaxe orixinal aínda que haxa erros na mensaxe recibida. Paira iso é necesario introducir máis información adicional redundante e, sobre todo, que todas as palabras ou números posibles que se poidan enviar no código teñan una distancia mínima entre si. Así, supoñamos que a distancia entre todos os caracteres posibles é de tres bits, se se produce un erro nun bit podemos saber con suficiente certeza cal era o carácter que se quería enviar, se a probabilidade de recibir dúas bits erróneos dun sinal é relativamente pequena. Desta forma, dependendo da fiabilidade da canle, realizaremos una maior ou menor distancia entre os sinais do código (número de bits) e introduciremos máis ou menos información redundante, pero o receptor poderá tamén reparar as mensaxes erróneas.
Os códigos que corrixen erros non os inventou Shannon. O seu compañeiro Richard Hamming era o pioneiro niso. Pero Shannon formalizou matematicamente a teoría dos códigos de corrección de erros e definiu o número máximo de bits adicionais necesarios paira diferentes probabilidades de fallo da canle. E esta formulación é a que utilizan todos os códigos capaces hoxe en día de emendar os erros, con miles de usos: nas comunicacións con naves espaciais e outras, no almacenamento de información en CDs e pendrives, etc.
Como vedes, as achegas de Shannon no artigo “A mathematical theory of communication” foron inxentes. Adiantóuselle moito o seu tempo, propuxo solucións a moitos problemas prácticos de futuro e todo dunha maneira moi elegante, con fórmulas e teoremas matemáticos e demostrando teoremas.
...e máis aínda

Ademais destas achegas principais, Shannon realizou outras moitas pequenas achegas. “Txiki”, por dicilo dalgunha maneira, xa que son pequenos en comparación con outras achegas, pero algunhas delas serían suficientes paira calquera outra fama.
II. Durante a Guerra Mundial, antes de escribir o seu coñecido artigo, Bell traballou en criptografía nos laboratorios e realizou algúns descubrimentos no campo da criptografía. Isto permitiulle coñecer a Alan Turing. Turing falou da idea da súa máquina universal, do concepto de computadores actuais, que, en definitiva, complementábase perfectamente coas ideas de Shannon. Naquela época, Shannon inventou diagramas de fluxo de sinais.
Shannon gustáballe o xadrez e tamén traballou niso. En 1950 escribiu un dos primeiros artigos sobre a problemática dos programas de xadrez dos computadores, que puxo en marcha a área. Neste artigo estimou que as combinacións posibles do xogo de xadrez son polo menos 10 120, o que hoxe se coñece como número de Shannon.
En 1950 realiza o rato automático Theseus, capaz de atopar a saída dun labirinto e aprende o camiño paira despois. Trátase do primeiro dispositivo de intelixencia artificial deste tipo. Tamén lle gustaban os malabarismos e nos anos 70 construíu o primeiro robot malabarista. Tamén construíu una máquina que resolvía o cubo de Rubik.
Nas súas viaxes ás Veigas xunto a algúns dos seus compañeiros gañou una fortuna, xa que, aplicando a teoría do xogo, contaban cartas e fabricaron un pequeno e escondible computador (o que algúns consideran o primeiro wearable) paira calcular probabilidades no xogo. E con métodos similares conseguiron gañar aínda máis en bolsa.
Shannon morreu en 2001, despois de sufrir o alzheimer nos últimos anos. Paira cando perdeu a conciencia da contorna, as súas achegas xa tiveron numerosas aplicacións, pero non tivo a oportunidade de coñecer o progreso e, sobre todo, a difusión que tiveron nos últimos anos Internet, os computadores e outros dispositivos. Seguramente se sorprendería. Como nós deberiamos sorprendernos, porque a persoa que permitiu levar a cabo este enorme cambio é case descoñecida.

Gai honi buruzko eduki gehiago
Elhuyarrek garatutako teknologia