Egunero ez ditu 24 ordu egunak

Demagun halako egun batean Eguzkiari begira zaudela, eta, kontu pixka batekin, haren posizioa markatzen duzula makila batekin, soka batekin edo eguzki-erloju batekin. Eguzkia, apurka-apurka, eskuinerantz mugituz joango da, ipar hemisferioan bazaude (I.H.), baina, zenbat denbora pasatuko da Eguzkia, biharamunean, berriz ere marka horretaraino iritsi arte?

Askok erantzungo duzue: “JUSTU-JUSTU HOGEITALAU ORDU!!”. Bada, BATEZ BESTE, BAI, baina segundo batzuetako aldea egon daiteke, urteko egunaren arabera, batzuetan Eguzkiak aurreratu egiten baitu, eta beste batzuetan, atzeratu.

Segundo batzuk agian gutxi irudituko zaizkizue, baina kontutan izan, Eguzkia egunero-egunero segundo batzuk atzeratzen bada, pilatuz joango zaizkiola segundoak, eta, azkenean, pilatutako atzerapen edo aurrerapen hori nabarmena izan daiteke. Izan ere, hamasei minuturaino iristen da!

Denok dakigunez, udazkenean, arratsaldeetan, goizago iluntzen du egunero-egunero, eta, goizean, berriz, geroago argitzen du; eta udaberrian, alderantziz. “Nik uste nuen bi solstizioek mugatzen zituztela bi egoera horiek, urte-sasoiak bezala. Adibidez, negukoan, abenduak 21, “San Tomas”, gaurik luzeena zela, goizen iluntzen zuena eta beranduen argitzen zuena. Bada hori ez da horrela: abenduaren erdialdean hasten da luzatzen arratsaldeko argia, alegia, argiak gehiago irauten du. Santa Luzia (abenduak 13) aipatzen dute esaera zahar askok —Gotzon Garatek bilduak— [1], baina abenduaren 9–10 inguru da Eguzkia goizen sartzen den eguna: 17ak eta 36 minutuan, Bilbon [2]. Urteko beste edozein egunetan, negu zein uda, beranduago iluntzen du, eta, egun hori solstizioa baino hamabi egun lehenago da! Hala ere, oraindik, abenduaren erdialdean, goizeko egunsentia ez da goizago hasten; beranduago argitzen jarraitzen du egunak! Eguzkia beranduen irteten den eguna urtarrilaren 3a da, gutxi asko: 8ak eta 44 minutuan [2]. Konturatuta al zeunden horretaz?

Udako solstizioan ere —ekainaren 21a— beste horrenbeste: ez dira simetrikoak egunsentia eta ilunabarra. Eguzkia goizen ateratzen den eguna (egunsentirik goiztiarrena) ekainaren 15a da (6ak eta 31 minutuan [2]) eta Eguzkia beranduen sartzen den eguna, berriz, ekainaren 27a (21ak eta 56 minutuan [2]). Gaurik laburrena eta luzeena solstizioetan bertan izaten dira, bai, baina Eguzkia sartzeko eta ateratzeko orduak ez dira simetrikoak izaten, pilatutako atzerapen hori dela medio (bisurteek egun bat atzeratu edo aurreratu ditzakete hemen aipatutako datak, baina lau urtean behin errepikatzen dira; esate baterako, bi solstizioak abenduaren eta ekainaren 20tik 22ra bitartean gerta daitezke. Beste efektu txikiago batzuk aipatuko ditugu geroago). Halaber, Eguzkiaren argia aprobetxatzeko ordu-aldaketa ofizialak ez ditut kontutan hartzen (hori ere beste arazo bat da).

Nolakoa da, bada, Lurraren biraketa? Lurrak biratu egiten du bere ardatzaren, edo bere buruaren inguruan (errotazioa); gutxi gorabehera, egun batean bira bat, baina ez da zehatza. Bira bat eta pixka bat gehiago da, hain zuzen, Eguzkia berriz ere aurrez aurre atzematen duen arte (eguzki-eguna deritzo horri). Kontuan izan Lurrak, Eguzkiaren inguruko orbitan ere, bira bat egiten duela urtero (translazioa) eta, beraz, translazioan zehar, bira gehigarri hori irabazten joaten dela egunero-egunero errotazioa.

Urte osoan zehar Lurrak 365,25 + 1 bira ematen ditu, alegia, 366,25. Gogoratzen duzu Jules Verneren “Munduari itzulia 80 egunean”? Phileas Fogg abenturazaleak apustua irabazi egin zuen, ezustean, egun gehigarri horri esker [3–4].

Alegia, urte osoan bira bat gehiago emateko, bira baten 365,25rena biratu behar du egunero gehigarri gisa (0,25 bira horiek dira bisurteak eragiten dituztenak lau urtean behin, baina hori ere beste kontu bat da).

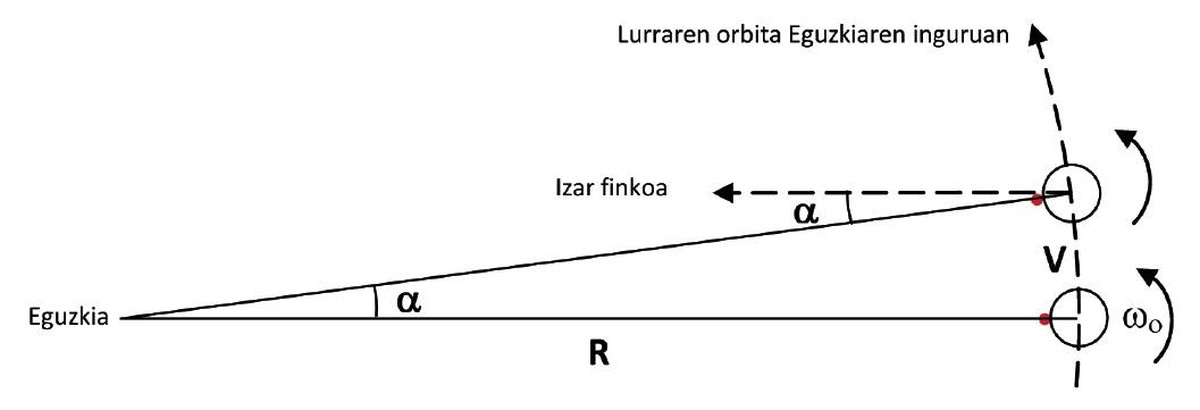
Beraz, 360 gradu/365,25 egun = 0,986 gradu/egun. Egun batean, Lurrak bira bat osorik eta 0,986 gradu gehiago egiten ditu (ia gradu bat gehiago. 1. irudian a izendatu da, beraz, egunero 361 gradu inguru biratzen da Lurra bere ardatzaren inguruan).

1. irudia. Lurrak, egun batean, bira bat eta eta pixka bat gehiago, a, egiten du.

Lurraren errotazioaren abiadura angeluarra hau da: w0 = 366,25 bira/365,25 egun = 1,002738 bira/egun beraz, bira bat eta pixka bat gehiago.

Eta Lurrak bira bakar bat osatzeko behar duen denbora: t = 1/w0 = 1/ 1,002738 = 0,99727 egun = 23 ordu 56 min 4 s (egun sidereoa deritzo horri).

Izan ere, Lurrak bira bat emateko, baina izar finkoekiko, ez ditu 24 ordu behar, 23 h 56 min 4 s baizik (horixe da egun sidereoaren iraupena); alegia, egun bat, lau minutu gutxiago. Adibidez, gauean izar finko bati ordu jakin batean begiratzen badiozu eta Lurrean erreferentzia finko bat hartzen baduzu, konturatuko zara izar horrek, biharamunean, ordu horretan, gradu bateko aurrerapena daukala (ia lau minutukoa, 2. irudiak erakusten duen bezala).

2. irudia. Lurrak bira bat osatzeko, izar finkoekiko, egun sidereo bat behar du, eguzki-egun bat baino lau minutu gutxiago. Ordu jakin batean begiratzen badiozu izarrari, konturatuko zara izar horrek, biharamunean, ordu horretan, gradu bateko aurrerapena daukala (lau minutu). Irudian, erreferentzia finkotzat zuhaitz jakin bat hartu da (izarrak ezkerretik eskuinera desplazatzen dira I.H.). Arg. Stellarium

Berriz ere 1. irudiari erreparatzen badiogu, eguzki-egun baten iraupena erraz kalkula dezakegu:

Biratutako Angelua = Abiadura Angeluarra · Denbora → 2p + a = w0· TE

Hemen, 2p + a, biratutako angelua da (2p, bira bat, radianetan eta, a, angelu gehigarria), w0 Lurraren errotazio-abiadura angeluarra eta TE, eguzki-egun baten iraupena. Berez, a angelu gehigarria ere egunaren iraupenaren mendekoa da, alegia, Lurrak egun batean osatzen duen angelua Eguzkiaren orbitan zehar:

a = V·TE /R

V Lurraren translazio-abiadura Eguzkiaren inguruan, eta R, Eguzkirainoko distantzia. Angelu gehigarri hori goiko ekuazioan ordezkatuz, honako adierazpen hau lortzen da eguzki-egunaren iraupenerako:

TE = 2p/(w0– V/R) (1)

Lurraren orbitak 150 milioi kilometro inguruko erradioa du, batez beste (R = 1.5 · 1011 m). Grabitazio unibertsalaren arabera, abiadura orbitala 30 km/s ingurukoa da (V = 3·104 m/s), batez beste. Beraz, V/R = 2·10-7 rad/s. Errotazio-abiadura angeluarra, unitate egokietan: w0 = 7.2922·10-5 rad/s. Kalkuluak eginez, eguzki-egunaren iraupen hau ateratzen zaigu: 86.400 s (÷60) = 1.440 minutu (÷60) = 24,00 h. Horregatik, gure erlojuek 24 orduko egunak neurtzen dituzte zehatz-mehatz, egunero-egunero berdin-berdinak, urteko edozein egunetan, horixe da-eta Eguzki-egun baten batez besteko iraupena.

Alabaina, adierazpen horretako bi magnitude, R eta V, ez dira konstanteak izaten urtean zehar. Horregatik, eguzki-egunaren iraupena ere (TE) ez da konstantea, aldakorra baizik, eta horregatik izaten du Eguzkiak atzerapena edo aurrerapena, erlojuekiko, urteko egunaren arabera. Gorabehera horien azalpenari “Denboraren ekuazio” deritzo [5–6].

Eguzkiaren atzerapen-aurrerapen horrek bi faktore ezberdin ditu:

Lurraren orbitaren eliptikotasuna

Lurraren orbita ez da zirkulua, elipsea baizik. Lurra Eguzkitik pixka bat urrunago dago afelioan eta hurbilago perihelioan. Izan ere, afelioa eta perihelioa ez dira solstizio-egunetan bertan, aste pare bat beranduago baizik: gutxi gorabehera, urtarrilak 4 eta uztailak 4 [7]. Eliptikotasuna txikia bada ere (e = 0.0167) distantziarik handiena eta txikiena honela kalkulatu behar dira: R · (1 ± e).

Bestalde, distantzia handiena duenean, hain zuzen ere, abiadurarik txikiena dauka Lurrak, eta distantzia txikiena duenean, abiadurarik handiena (Keplerren legearen edo Momentu Angeluarraren kontserbazioaren arabera): V · (1 ± e).

V/R terminoak balio minimoa atzematen du afelioan (a angelu minimoa) V/R = 1.934·10-7 rad/s, eta balio maximoa perihelioan (a angelu maximoa) V/R = 2.067·10-7 rad/s. Bata eta bestea eguzki-egunaren iraupenean ordezkatzen baditugu, (1) ekuazioan, 8 segundo luzeago ematen du perihelioan batez bestekoak baino, eta 8 segundo laburrago ematen du afelioan batez bestekoak baino (7.9 segundo dira, baina hamarrenak ez ditugu zehaztuko).

Beraz, orbitaren eliptikotasunaren eraginez, eguzki-egunaren iraupenak oszilatu egiten du; 24 ordu balioko du, doi-doi, urtean bi egunez bakarrik, afelioaren eta perihelioaren arteko erdiko egunetan hain juxtu (apirilak 5 eta urriak 3 inguru). Perihelioan, berriz (urtarrilak 4 inguru), 24 ordu baino zortzi segundo gehiago iraungo du, eta afelioan, berriz, zortzi gutxiago (uztailak 4 inguru).

Hirugarren irudiko marra beltzak erakusten du eguzki-egunak duen atzerapena batez besteko egunarekiko, urteko eguna zein den (0–365). Gutxi gorabehera, “sinu”formakoa da, 8 segundoko anplitudea dauka eta urtebeteko periodoa. Urriaren “3an” abiatzen da (0 eguna), perihelioan dauka maximoa (erlojuak baino atzeratuago dabil Eguzkia), apirilaren “5ean” berriz ere nulu bilakatzen da (182 eguna), afelioan minimoa (erlojuak baino aurrerago dabil Eguzkia) eta, 365. egunean, berriz abiatzen da zikloa.

3. irudia. Lurraren orbitaren eliptikotasunari dagozkion atzerapen-kurbak, urteko egunaren arabera (0-365. 0 eguna, urriaren 3a). Kurba beltza eta ezkerreko ardatza: eguzki-egunak egun batean erlojuekiko duen atzerapena (segundotan). Gehienez zortzi segundo inguru, egun bakar batean. Kurba gorria eta eskuineko ardatza: eguzki-egunaren eguneroko atzerapenek erlojuekiko pilatu duten atzerapen totala (minututan). Gehienez, zortzi minutu inguru.

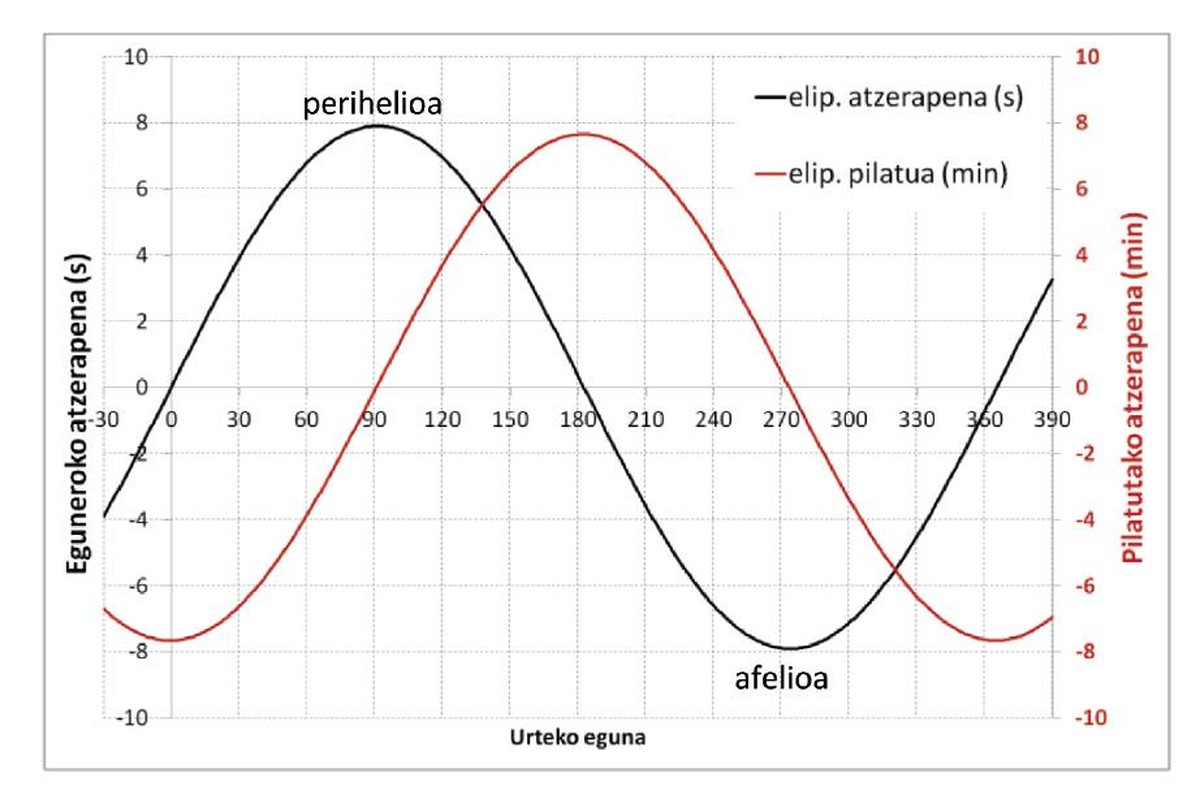
Zortzi segundoko atzerapenak txikia dirudi; baina hurrengo egunean ere beste zortzi segundo atzeratuko ditu, eta hurrengoan, eta hurrengoan (atzerapena gutxituz doan arren). Eta atzerapenak pilatuz joango dira, egunero-egunero, eta pilatutako atzerapen totala kalkulatzeko, urte-erdiko atzerapenen batuketa egin behar da (edo sinu funtzioaren integrala urte-erdian). Eta pilaketa hau ematen du:

DTE(pilatuta) = DTEmax· 365,25/2p = 8 s · 365,25/ 2p = 465 s = 7 min eta 45 s

Ia zortzi minutuko atzerapena pilatzen du Eguzkiak urte-erdian!

Hirugarren irudiko marra gorriak erakusten du Eguzkiak erlojuekiko pilatutako atzerapena, urteko eguna zein den (eta eskuineko ardatzeko balioak). Urriaren 3an abiatuta (0 eguna, eta aurreko hilabeteetako pilaketak kontuan hartuta), –8 minutuko atzerapenetik abiatzen da (+8ko aurrerapenetik), pilatutako atzerapena handituz doa eta perihelioan nulu bilakatzen da (urtarrilak 4 inguru). Ondoren, atzerapenak pilatzen segitzen du urte-erdia pasa arte eta, orduan, apirilaren 5ean, ia zortzi minutu pilatu dira. Gero, Eguzkia aurreratzen hasten da (atzerapen negatiboa). Pilatutako atzerapena jaitsiz doa, eta berriz ere afelioan (uztailak 4 inguru) nulu bilakatzen da. Berriz, urriaren 3ra arte (365. egunean), atzerapenak negatibo izaten segitzen du (aurrerapena) eta justu amaieran, –8 minutuko atzerapena pilatu da.

Afelioa eta perihelioa, urte luzeetan zehar, desplazatzen ari dira Eguzkiaren planoaren inguruan eta, beraz, ekinokzioak ere bai. Fenomeno horri “apsideen prezesioa” deritzo. Ziklo bat osatzen dute 26.000 urtean, alegia, 50 arku segundo urtero. Zenbait efekturen gainezarpenak eragiten du hori, erlatibitatearen teoria orokorra ere barne dela[8].

Eguzki-egunaren atzerapen-aurrerapenak beste faktore bat ere badu:

Lurraren errotazioaren inklinazioa

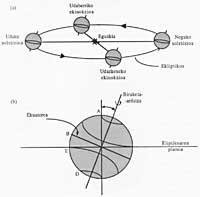
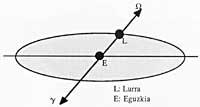
Lurraren errotazioaren planoa (Ekuatorea) eta Lurraren orbita (Ekliptika) ez dira paraleloak: 23,5° osatzen dute elkarrekiko [9]. Angelu horrek eragiten ditu, hain zuzen ere, urte sasoiak. Laugarren Irudiak erakusten du Ekliptika, ia orbita zirkularra, eta Ekuatorea, plano karratu gisa irudikatuta, Lurrarekin batera lau posiziotan: bi solstizioetan (ezkerrean, udakoa, eta eskuinean, negukoa I.H.) eta bi ekinokzioetan (aurrean, udazkenekoa, eta atzean, udaberrikoa). Bi planoen arteko angeluari d deituko diogu.

4. irudia. Lurraren translazioa (Ekliptika) eta errotazioa (Ekuatorea) ez dira paraleloak: 23,5°-ko angelua osatzen dute. Eguzki-egunaren iraupena kalkulatzeko (1 ekuazioa), Ekuatorea hartu behar dugu erreferentzia gisa (ezker-eskuin osagaia soilik neurtu behar dugulako, alegia, Eguzkia meridiano berera iristea, eta ez bere desplazamendu bertikala); beraz, Lurraren V eta Lurraren R Ekuatorearen planora proiektatu behar dira.

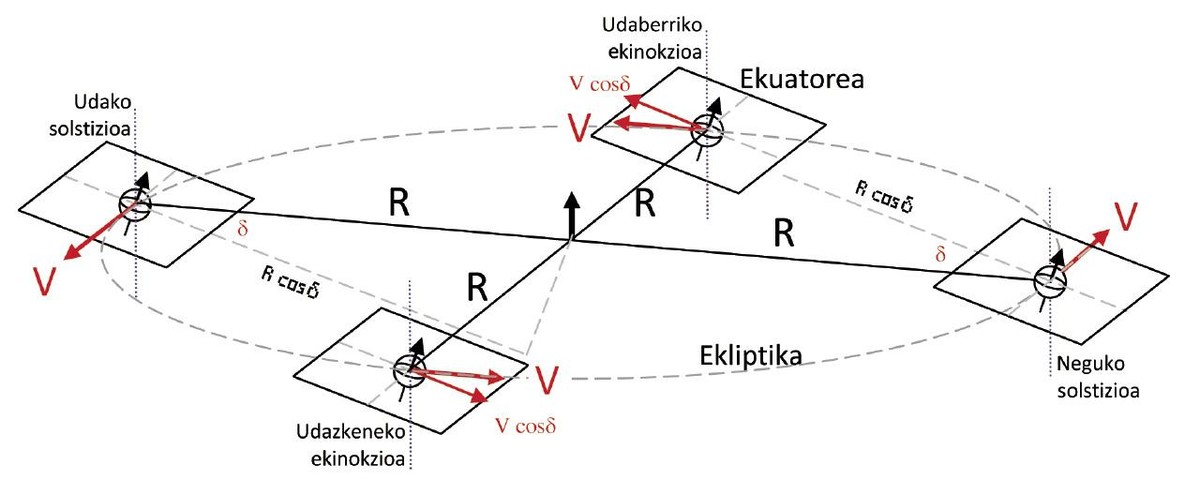
Eguzkia egun batetik bestera, pixkanaka, desplazatu egiten da zeruan, izar finkoekiko, eta ez da soilik ezker-eskuin desplazatzen: gora eta behera ere bai. Eguzki-egunaren iraupena kalkulatzeko, Eguzkiaren abiaduraren osagai horizontala bakarrik hartu behar da kontuan, alegia, meridiano berera iristeko behar duen denbora. Eguzkiaren desplazamendu bertikalak ez du eraginik ordua kalkulatzeko. Abiadura-bektorea, V, bi solstizioetan, Ekuatorean datza, beraz, osorik da horizontala, baina bi ekinokzioetan d angelua osatzen du Ekuatorearekiko, eta desplazamendu bertikala maximoa da. Horregatik, Lurretik ikusita, solstizioetan maximoa da Eguzkiaren abiadura horizontala (V) eta bi ekinokzioetan minimoa (V·cosd); horregatik, osagai horrek urtero bi maximo dauzka eta bi minimo, edo urte-erdiko periodoa.

Bestalde, R bektorea Ekuatorean datza bi ekinokzioetan; bi solstizioetan, berriz, d angelua osatzen du Ekuatorearekiko. Beraz, R distantziaren proiekzioa maximoa izango da urtean bi aldiz (ekinokzioetan, R), eta minimoa beste bitan (solstizioetan, R·cosd). Ikusten denez, efektu horrek ere urte-erdiko periodoa dauka [10].

Denetara, (1) ekuazioan, eguzki-egunaren iraupena kalkulatzeko, R-ren ordez R·cosd ordezkatu behar da, eta V-ren ordez, V·cosd, baina ez biak aldi berean: iraupen maximoa kalkulatzeko, V abiaduraren proiekzioa maximoa denean, eta R posizioarena minimoa, alegia, bi solstizioetan:

2p/(w0 – V/R) = 2p/(w0 – V/R·cosd) ≈ 86420 s

eta iraupen minimoa, V abiaduraren proiekzioa minimoa denean eta R-rena maximoa, alegia, bi ekinokzioetan:

2p/(w0 – V/R) = 2p/(w0 – V·cosd/R) ≈ 86380 s

Beraz, eguzki-egunaren iraupenak hogei segundo gehiago dauzka (erlojuen 24 orduak baino) bi aldiz urtean (solstizioetan), eta hogei segundo gutxiago urtean beste bi aldiz (ekinokzioetan) (20,3 segundo dira, baina hamarrenak ez ditugu zehaztuko).

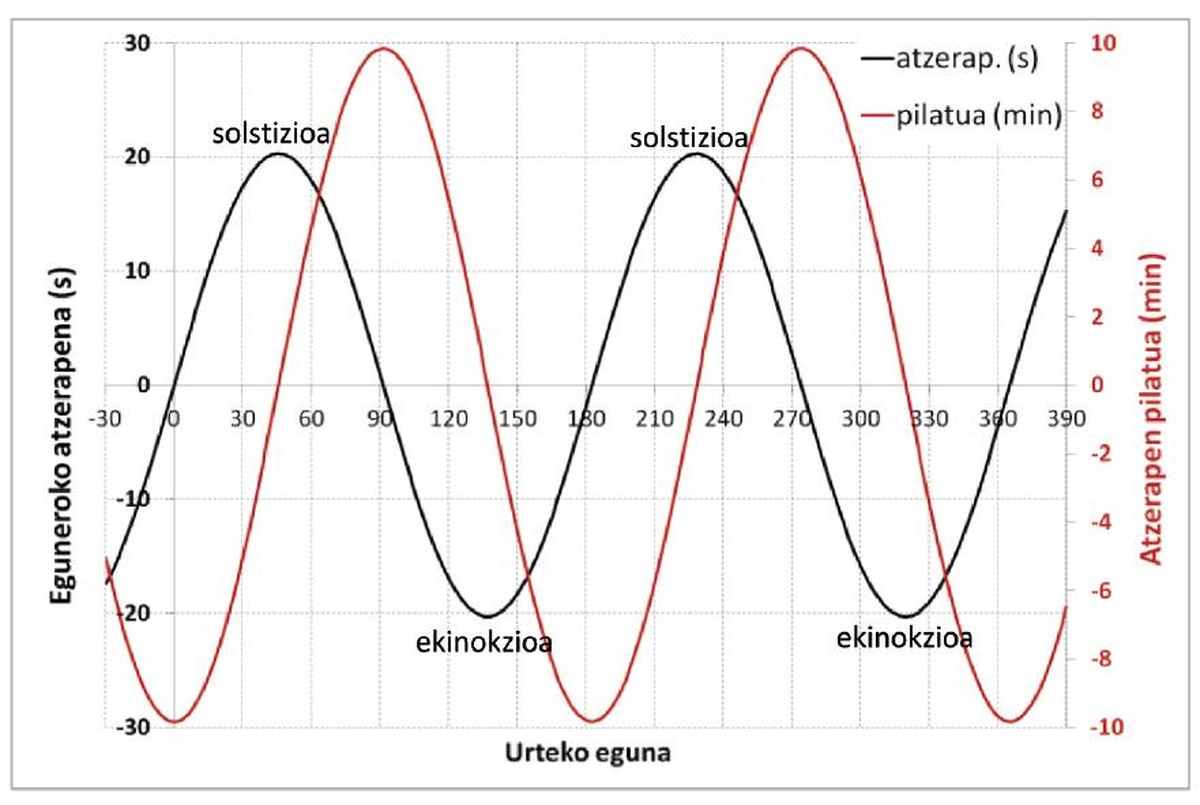
Bosgarren irudiko marra beltzak erakusten du eguzki-egunak duen atzerapena, batez besteko egunarekiko eta urteko eguna zein den (0–365). Gutxi gorabehera, “sinu” formakoa da, 20 segundoko anplitudea dauka eta urte-erdiko periodoa. Urtean lau aldiz da nulua: solstizioen eta ekinokzioen arteko erdiko egunetan; bi solstizioetan dauka maximoa (erlojuak baino atzeratuago dabil Eguzkia), eta bi ekinokzioetan minimoa (erlojuak baino aurrerago Eguzkia).

Eliptikotasunaren kasuan bezalaxe, hogei segundoko atzerapena pilatuz joaten da, egunero-egunero, eta pilatutako atzerapen totala kalkulatzeko, urte-laurdeneko atzerapenen batuketa egin behar da (edo sinu funtzioaren integrala urte-laurdenean). Eta pilaketa hau ematen du:

DTE(pilatuta) = DTEmax· 365,25/4p = 20 s · 365,25/4p = 581 s = 9 min eta 41 s

Ia hamar minutuko atzerapena pilatzen du Eguzkiak urte-laurdenean!!

Bosgarren irudiko marra gorriak erakusten du Eguzkiak erlojuekiko pilatutako atzerapena, urteko egunaren arabera (0-365; 0 eguna, azaroak 6 inguru, eta eskuineko ardatzeko balioak). Urtean lau aldiz da nulua: bi solstizioetan eta bi ekinokzioetan. Justu solstizioen eta ekinokzioen arteko erdiko egunetan, balio maximoak eta minimoak hartzen ditu: –10 minutuko atzerapena (= +10-eko aurrerapena), eta alderantziz. Urte-erdia pasatzen den bakoitzean, berriz abiatzen da zikloa.

Ekuatoreak Ekliptikarekiko daukan inklinazioari dagokio efektu hori, baina, gaur egun, inklinazioa gutxitzen ari da, Lurraren errotazio-ardatzaren “nutazioa” dela-eta, baina erritmo motela dauka: gaur egun, 0,2 gradu gutxitzen ditu 2.000 urtean [9].

5. irudia. Lurraren Ekuatorearen inklinazioari dagozkion atzerapen-kurbak urteko egunaren arabera (0-365, 0 eguna, azaroaren 6a). Kurba beltza eta ezkerreko ardatza: eguzki-egunak egun batean duen atzerapena erlojuekiko (segundotan). Gehienez, hogei segundo inguru. Kurba gorria eta eskuineko ardatza: eguzki-egunaren eguneroko atzerapenek pilatu duten atzerapen totala erlojuekiko (minututan). Gehienez, hamar minutu inguru.

Bi efektuak batera (Denboraren ekuazioa)

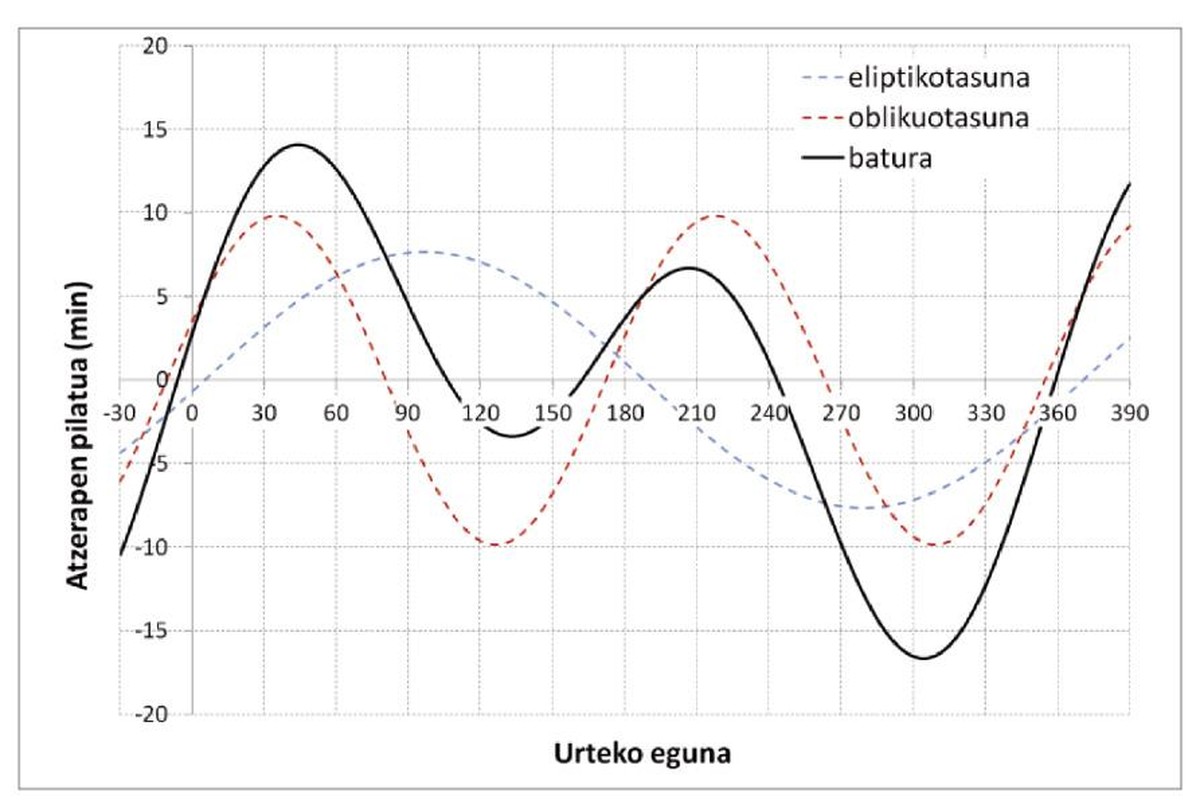
Eguzki-egunaren “atzerapen pilatuak” elkartzen baditugu, batetik, orbitaren eliptikotasuna eta, bestetik, Ekuatorearen inklinazioa, “sinu” formako bi funtzioen batura egin behar dugu. Lehenak, zortzi minutuko anplitudea eta urtebeteko periodoa du, eta bigarrenak, hamar minutuko anplitudea eta urte-erdiko periodoa. Gainera, bi funtzioen fasea ez da aldi berean abiatzen: lehena nulua da perihelioan (urtarrilak 4 inguru), eta bigarrena nulua da solstizioan (abenduak 21).

Bi kurba horien baturak ziklo bitxi samarra ematen du, 6. irudiak erakusten duen bezala, non eguzki-egunaren erlojuekiko atzerapen pilatua urteko egunaren arabera (0-tik 365-ra; 0 eguna, urtarrilak 1) adierazten den. Ikusten denez, urtean lau aldiz dabil Eguzkia doi erlojuekin (24 ordu). Hona gutxi gorabeherako datak: apirilak 15, ekainak 13, irailak 1 eta abenduak 25. Bi tartetan atzeratuta dabil (abendutik apirilera eta ekainetik irailera), eta beste bitan, aurreratuta (apiriletik ekainera eta irailetik abendura). Bi maximo dauzka: otsailak 11 (14,26 minutu) eta uztailak 26 (6,48 minutu), eta bi minimo: maiatzak 14 (–3,69 minutu) eta azaroak 3 (–16,41 minutu).

6. irudia. Bi atzerapenen efektuak elkartuta: batetik, eliptikotasunak ia zortzi minutuko oszilazioa eragiten du, urte osoko periodoaz, eta perihelioan abiatzen da (marra urdina). Bestetik, Ekuatorearen inklinazioak ia hamar minutuko oszilazioa eragiten du, urte-erdiko periodoaz, eta solstizioan abiatzen da (marra gorria). Eta bi efektuen batura: marra beltza edo “denboraren ekuazioa”.

Erreferentziak

ANALEMMA

Eguzkiari urte osoan zehar ateratako argazkien sekuentzia. Eguerdian atera dira argazki guztiak. Eguneko beste ordu bat aukeratuz gero, “zortzikoa” inklinatuta ateratzen da. Arg. Craig Lent

Egunero ordu berean eta toki berean argazki bat ateratzen badiogu Eguzkiari, “analemma” deritzon “zortziko formako” ibilbide bat egiten duela ikusiko dugu.

Zortzikoaren altuera maximoa eta minimoa tokiaren latitudea gehi eta ken Lurraren ardatzaren inklinazioa dira (23,5o) (eta urte-sasoiak eragiten dituena); “zortziko formako” ibilbidearen zabalera, berriz, Eguzkiaren ezker-eskuineko atzerapen eta aurrerapen pilatuak: ez da simetrikoa; goiko biribilak -4 minutu, eta +6 minutu, eta behekoak -16 minutu eta +14 minutu (gradu bat, lau minutu) [11].