Ecuaciones diferenciales en busca de estabilidad

2009/11/01 Alberdi Celaya, Elisabete - Matematikan lizentziatua eta doktoregaia Iturria: Elhuyar aldizkaria

• Matematika

También en matemáticas hay disciplinas en las que la estabilidad es fundamental. Los que queremos fijarnos tienen cabida en los programas de las carreras científicas y técnicas, se utilizan en la formulación de modelos matemáticos y para algunos se busca un resultado analítico, mientras que otros se resuelven con métodos numéricos --aproximaciones - y con el ordenador como acompañante. A algunos alumnos les gusta, pero a la mayoría les causan quebraderos de cabeza. ¿Qué son? Son ecuaciones diferenciales. Las ecuaciones diferenciales, al igual que el ser humano en la vida, buscan el mayor campo de estabilidad posible.

Utilidad de las ecuaciones diferenciales

Un modelo matemático es un dispositivo que describe un sistema o suceso de la vida. La formulación de un modelo matemático comienza con la identificación de las variables que influyen en el sistema, es decir, producen un cambio en el sistema. A continuación se establecen hipótesis razonables sobre el sistema, identificando las leyes empíricas aplicables. Algunas de estas hipótesis indican la medida de la variación de algunas de las variables previamente definidas. El enunciado matemático de estas hipótesis será una ecuación o un sistema de ecuaciones en el que aparezcan las derivadas, que es el sistema de ecuaciones diferenciales.

Su resolución concreta nos permitirá conocer el comportamiento del sistema. Pero, ¿de qué hablamos cuando hablamos de modelo o modelo matemático?

En la cinética de las reacciones químicas interesa su evolución a lo largo del tiempo. Al ser las velocidades derivadas del tiempo de cualquier variable, la cinética de las reacciones se modeliza mediante ecuaciones diferenciales. Ejemplo de ello es el caso de que ambas sustancias generan un tercero. Las variables son concentraciones de sustancias, mientras que las leyes empíricas son la ley de acción de masas y la ley de conservación de masas. La primera nos dice que el producto de las concentraciones de los reactivos es proporcional al producto de las concentraciones de los productos, y las segundas, la suma de las masas de los reactivos es igual a la de los productos.

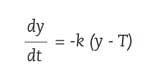
En la refrigeración de los cuerpos también se utilizan ecuaciones diferenciales. Por ejemplo, si sacamos un pastel del horno a 150ºC y queremos saber su temperatura en cualquier momento. Si estamos investigando el homicidio o el asesinato de una persona y queremos calcular a qué hora murió, utilizaremos la ley de refrigeración de Newton. Esta ley establece que el cambio de temperatura de la superficie corporal es proporcional a la diferencia entre la temperatura corporal y la temperatura ambiente. Así, si la temperatura del cuerpo en el instante t es y ( t ) y la temperatura en el medio T, según la ley de Newton, se cumplirá la siguiente ecuación diferencial:

siendo k 0 la proporcionalidad constante.

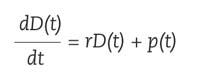
¿Queremos calcular los intereses que nos dará una cantidad de dinero que ingresamos en el banco? Deberemos utilizar ecuaciones diferenciales. Supongamos que introducimos en el banco la cantidad D 0 y nos pagan un tipo de interés r. Llamaremos D ( t ) a la cantidad que tendremos dentro de t años. La variación de la cantidad será la suma de la variación por acumulación de intereses y la variación de ingresos que realizamos en el banco, p de fórmula.

Hay, por tanto, que modelar en la vida cotidiana utilizando ecuaciones diferenciales.

Dificultades de resolución

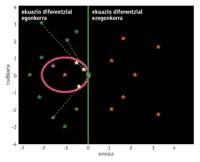
Una vez obtenida la ecuación diferencial se debe resolver. En ocasiones, no es posible su liberación analítica, y mediante métodos numéricos se obtiene un resultado aproximado. Las ecuaciones diferenciales incluyen unos autovalores complejos que denominaremos l. Cuando la parte real de estos autovalores es positiva, la ecuación diferencial es inestable y el resultado aproximado que obtendríamos utilizando un método numérico para su liberación no tiene por qué parecerse a la solución real, ya que un pequeño cambio tiene un fuerte impacto en ellos. Por ello, los métodos numéricos se aplican a ecuaciones diferenciales estables, autobalioides de parte real negativa. Por otra parte, el propio método también tiene una zona de estabilidad. Y si se quiere conseguir un buen resultado, los autovalores deben situarse allí. Por tanto, los autovalores de las ecuaciones diferenciales estables no presentes en esta zona se trasladan a la zona de estabilidad, multiplicando los autovalores por un número h medido (0,1) que denominaremos medida del paso.

La medida del paso es fundamental para resolver la ecuación y, por supuesto, no puede ser cualquier número. En términos de fiabilidad, el método de resolución debe ser lo suficientemente pequeño como para mantenerse dentro de la zona de estabilidad y lo suficientemente grande como para dar el menor número de pasos posibles de cara al trabajo. ¿Cómo conseguir ese equilibrio?

Equilibrio del área de estabilidad

Para saber qué pasos se pueden dar en el método numérico hay que fijarse en el error. Al utilizar métodos numéricos se genera un error local en cada paso. Pero hay otro error que aparece en la longitud, que es la reproducción de los errores de cada paso, y que está formado por las potencias de un número llamado factor de amplificación. Para evitar el aumento del error, el factor de amplificación debe ser menor que la unidad. La zona que cumple esta condición es la conocida como zona de estabilidad del método. Pues bien, el autovalor l debe estar en la zona de estabilidad tras multiplicarse por h para que el factor de amplificación sea menor que la unidad. Pero no sólo eso, una vez que el producto l .h se encuentra en la zona de estabilidad, se ve si el número h debe ser menor, ya que cualquier número que sea menor que h que hemos encontrado hace posible que después de multiplicar el autovalor se lleve a la zona. De los números que permiten llevar el autovalor al campo, el número h que mantiene el error local dentro de una tolerancia es el que se elige como medida del paso. Esta medida de paso permite tener controlados los dos errores (local y longitudinal). Cuanto mayor sea este número, mayor será el número de pasos que podremos dar y más rápido será el resultado, un objetivo que el gran campo de estabilidad permite alcanzar.

Pero la medida de la zona de estabilidad también está condicionada. Depende del orden. El orden es el parámetro que se utiliza para medir la precisión del método y es más preciso cuanto más alto es el orden. Normalmente, a medida que aumenta el orden, la zona de estabilidad disminuye. Esto nos obliga a dar pasos menores, aunque el resultado sea más preciso.

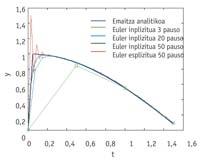
El propio método también condiciona la medida de la zona de estabilidad. Los métodos implícitos suelen tener un área de estabilidad mayor que los explícitos, pero también presentan desventajas: la principal es que se requieren operaciones más o menos complejas que en los métodos explícitos. Por ello, cuando los autovalores no son muy grandes, se prefiere el método explícito, ya que las operaciones a realizar serán más sostenibles.

El sueño sería encontrar la máxima estabilidad en órdenes altos y métodos explícitos, pero tampoco en este campo de la ciencia hay rareza. Con el fin de conseguir que las ecuaciones diferenciales se suelten fácilmente por métodos numéricos, son numerosos los trabajos realizados para aumentar el campo de estabilidad. Los primeros son los métodos de Adams Bashforth y Moulton, en los que se utiliza tanto la información del último paso como la información de otros pasos más rápidos para construir el siguiente paso. De esta forma se consiguió subir el orden del método numérico, y el de orden 1 tiene un campo mayor que el de Euler explícito (también de orden 1). Una de las propuestas más importantes fue la denominada BDF (fórmula backward differentiation) realizada por Gear hacia 1971, un método implícito que utilizaba información en varios pasos más ligeros. El método BDF consiguió que las zonas de estabilidad fueran también importantes en órdenes elevados. Últimamente predominan los métodos que utilizan la derivada 2 o los llamados puntos de superfuturo, ya que tienen grandes áreas de estabilidad, aunque incrementan el trabajo a realizar en cada paso.

Muchos pequeños pasos o pocos grandes pasos, ahí está la clave. En esta competencia, la primera opción, con muchos pequeños pasos, tiene la ventaja de la fiabilidad y la segunda la optimización del trabajo. Unificar ambas opciones en una sola ocasión sería excelente, ya que se conseguiría "fiabilidad sin trabajo excesivo". La clave para romper este equilibrio radica en métodos de gran campo de estabilidad, que no ponen límites tan rígidos a la medida del paso. Por eso es posible dar pasos no tan fiables y grandes pasos fiables.