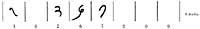Com operar? (I). Suma i resta

1990/10/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

En números anteriors ens submergim en la història de les xifres. Allí vam veure els sistemes utilitzats per l'home. El que va motivar a inventar-se les xifres va ser la necessitat de comptar (i també les operacions relacionades amb el còmput). Però, fins que apareixia el nostre sistema, com es resolien les operacions? Aquest article tracta sobre aquesta pregunta. Les petjades oposades ens permeten aproximar-nos a la forma en què l'home ha calculat.

El que li va portar a inventar-se els números, com s'ha dit, va ser la necessitat de comptar. El comptatge es feia amb el cos. Encara que en alguns casos s'utilitzaven a més de la mà altres parts del cos (peus, braços, cara, ...), es pot dir que la primera calculadora humana va ser la mà. La mà, probablement, va crear les bases deu, cinc, dotze i vint. A més de comptar manualment, l'home realitzava operacions. En aquella època, hem de recordar que l'ésser humà no entenia ni coneixia cap número escrit. No obstant això, era capaç de realitzar diverses multiplicacions.

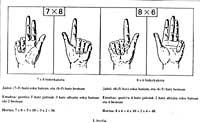
Per exemple, per a multiplicar dos números entre 5 i 10, en una mà baixaven tants dits com un producte i la diferència entre 5, en l'altra el producte i el 5. El resultat s'obtenia multiplicant el nombre de dits rebaixats en les dues mans per deu (de cap) i sumant-se al producte de la quantitat de dits sense baixar en totes dues mans (Figura 1).

Això té la seva verificació matemàtica: si x e i són números compresos entre 5 i 10, en una mà (x-5) descendeixen els dits (i-5) i en l'altra (i-5) i sense descendir, en la primera hi ha 5 - (x-5) i en la segona hi ha 5 - (i-5), sent el nombre de dits baixats (x-5) + (i-5). Realitzant les operacions esmentades 10 [(x-5) + (i-5)] + [5 - (x-5)] . [5 - (i-5)] = 10 (x+i-10) + (10-x) . Tenim (10-i) = 10x + 10y - 100 + 100 - 10x - 10y + xy = xy.

Una regla similar servia per a multiplicar dos números entre 10 i 15 o dos números entre 15 i 20, etc.

Per a multiplicar dos números entre 10 i 15, en cada mà es flexionaven tants dits com un producte i la diferència entre 10; es multiplicaven per 10 el nombre de dits agacados; després es multiplicaven els dits que havien baixat en dues mans i finalment se sumaven els dos resultats i 100.

Tots aquests llençols tenen la seva verificació matemàtica, encara que l'home de llavors no ho entengui.

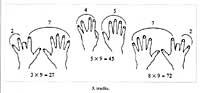
Com a curiositat indicarem manualment la taula de multiplicació del número 9. Obrint les dues mans davant de nosaltres, d'esquerra a dreta, després de donar als dits els valors 1, 2, 3, ..., ajupirem el dit corresponent al número que indica l'altre producte que té com a producte 9 i ens donarà el resultat el nombre de dits que queden a cada costat d'aquest dit; el costat esquerre el decimal i el dret la unitat (figura 3).

Però anem ara a veure les primeres operacions escrites. Abans de començar, aclarirem que no usarem les xifres actuals.

Suma

És sens dubte l'operació més senzilla, tant teòrica com pràctica. Veurem alguns exemples al llarg de la història d'aquesta operació.

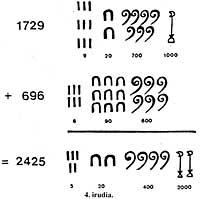
Perquè els Egypti sumin dos números, com 1729 i 696, escrivint sobre la cançó

(Figura 4). Després es recollien els mateixos símbols i s'obtenia el resultat de substituir 10 símbols d'un ordre per un d'ordre següent.

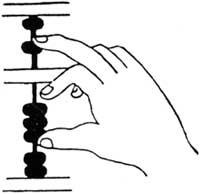
Un altre exemple ve de la mà de l'abaco. En l'àbac, per a unir dos números s'escrivien els dos a través de cants, després del bateig, i el resultat apareixia després de fer els resums necessaris. Un àbac especial, realitzat en la sorra mitjançant columnes, va ser utilitzat per hindús que eren hàbils en el càlcul. En cada columna escrivien un número, deixant la columna buida per a indicar zero o desordre. La suma es realitzava com l'altre àbac, però substituint els cants pels números. D'aquí ve l'algorisme que nosaltres utilitzem ara.

No obstant això, els hindús tenien un altre algorisme, l'anomenada reculada. Això (els números que s'agrupaven per columnes començant per l'esquerra) consistia a esborrar la portada quan estaven les k (figura 5).

XVI. En 1540, Gemma Frisius va crear un algorisme. Escrivia els números de major a menor i de dalt a baix i unia els números de cada columna. Els resultats parcials així obtinguts s'escrivien de dreta a esquerra i els recollien (figura 6).

Com pots comprovar, la major diferència entre els diferents algorismes estava en l'expressió de resultats.

Resta

El que fa interessant aquesta operació és el cas en el qual el restador és major que el minuend, però no entrarem en ell. L'algorisme de la sostracció no estava estandarditzat. Existeixen molts mètodes per a realitzar aquesta operació. No obstant això, la idea de la demanda de formació és antiga i estesa. El mètode, o idea, va ser utilitzat per Fibonacci (Leonardo de Pisa) en 1202.

No obstant això, portarem l'algorisme de Columbia que evita demanar preparació. En el següent exemple es pot calcular la diferència 8432-5976 segons l'algorisme de Columbia: