Como operar? (I). Suma e resta

1990/10/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

En números anteriores mergullámonos na historia das cifras. Alí vimos os sistemas utilizados polo home. O que motivou a inventarse as cifras foi a necesidade de contar (e tamén as operacións relacionadas co cómputo). Pero, ata que aparecía o noso sistema, como se resolvían as operacións? Este artigo trata sobre esta pregunta. As pegadas atopadas permítennos aproximarnos á forma en que o home calculou.

O que lle levou a inventarse os números, como se dixo, foi a necesidade de contar. O cálculo facíase co corpo. Aínda que nalgúns casos utilizábanse ademais da man outras partes do corpo (pés, brazos, cara, ...), pódese dicir que a primeira calculadora humana foi a man. A man, probablemente, creou as bases dez, cinco, doce e vinte. Ademais de contar manualmente, o home realizaba operacións. Naquela época, debemos lembrar que o ser humano non entendía nin coñecía ningún número escrito. Con todo, era capaz de realizar varias multiplicacións.

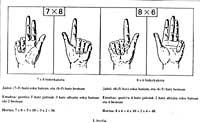
Por exemplo, paira multiplicar dous números entre 5 e 10, nunha man baixaban tantos dedos como un produto e a diferenza entre 5, na outra o produto e o 5. O resultado obtíñase multiplicando o número de dedos rebaixados nas dúas mans por dez (de cabeza) e sumándose ao produto da cantidade de dedos sen baixar en ambas as mans (Figura 1).

Isto ten a súa verificación matemática: si x e e son números comprendidos entre 5 e 10, nunha man (x-5) descenden os dedos (e-5) e na outra (e-5) e sen descender, na primeira hai 5 - (x-5) e na segunda hai 5 - (e-5), sendo o número de dedos baixados (x-5) + (e-5). Realizando as operacións mencionadas 10 [(x-5) + (e-5)] + [5 - (x-5)] . [5 - (e-5)] = 10 (x+e-10) + (10-x) . Temos (10-e) = 10x + 10e - 100 + 100 - 10x - 10e + xy = xy.

Una regra similar servía paira multiplicar dous números entre 10 e 15 ou dous números entre 15 e 20, etc.

Paira multiplicar dous números entre 10 e 15, en cada man se flexionaban tantos dedos como un produto e a diferenza entre 10; multiplicábanse por 10 o número de dedos agacados; logo multiplicábanse os dedos que baixaran en dúas mans e finalmente sumábanse os dous resultados e 100.

Todas estas sabas teñen a súa verificación matemática, aínda que o home de entón non o entenda.

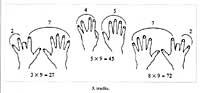
Como curiosidade indicaremos manualmente a táboa de multiplicación do número 9. Abrindo as dúas mans diante de nós, de esquerda a dereita, despois de dar aos dedos os valores 1, 2, 3, ..., agacharemos o dedo correspondente ao número que indica o outro produto que ten como produto 9 e daranos o resultado o número de dedos que quedan a cada lado dese dedo; o lado esquerdo o decimal e o dereito a unidade (figura 3).

Pero imos agora a ver as primeiras operacións escritas. Antes de empezar, aclararemos que non imos usar as cifras actuais.

Suma

É sen dúbida a operación máis sinxela, tanto teórica como práctica. Veremos algúns exemplos ao longo da historia desta operación.

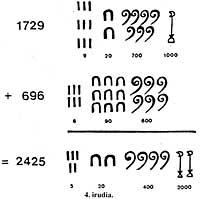
Para que os Egypti sumen dous números, como 1729 e 696, escribindo sobre a canción

(Figura 4). Logo recollíanse os mesmos símbolos e obtíñase o resultado de substituír 10 símbolos dunha orde por un de orde seguinte.

Outro exemplo vén da man do abaco. No ábaco, paira unir dous números escribíanse os dous a través de cantos, tras o bautizo, e o resultado aparecía despois de facer os resumos necesarios. Un ábaco especial, realizado na area mediante columnas, foi utilizado por hindús que eran hábiles no cálculo. En cada columna escribían un número, deixando a columna baleira paira indicar cero ou desorde. A suma realizábase como o outro ábaco, pero substituíndo os cantos polos números. De aquí vén o algoritmo que nós utilizamos agora.

Con todo, os hindús tiñan outro algoritmo, o chamado retroceso. Isto (os números que se agrupaban por columnas comezando pola esquerda) consistía en borrar a levada cando estaban as k (figura 5).

XVI. En 1540, Gemma Frisius creou un algoritmo. Escribía os números de maior a menor e de arriba abaixo e unía os números de cada columna. Os resultados parciais así obtidos escribíanse de dereita a esquerda e recollíanos (figura 6).

Como podes comprobar, a maior diferenza entre os distintos algoritmos estaba na expresión de resultados.

Resta

O que fai interesante esta operación é o caso no que o restador é maior que o minuendo, pero non imos entrar nel. O algoritmo da subtracción non estaba estandarizado. Existen moitos métodos paira realizar esta operación. Con todo, a idea da demanda de formación é antiga e estendida. O método, ou idea, foi utilizado por Fibonacci (Leonardo de Pisa) en 1202.

Con todo, imos traer o algoritmo de Columbia que evita pedir preparación. No seguinte exemplo pódese calcular a diferenza 8432-5976 segundo o algoritmo de Columbia: