Fourier Transform

2002/10/01 Roa Zubia, Guillermo - Elhuyar Zientzia Iturria: Elhuyar aldizkaria

• Matematika

What's behind the expensive team of scientists? How do you process the data that these machines receive? In general, we don't care much. A computer will collect the measurements and reflect the results using a modern graph. In addition, the more expensive the tooling, the more accurate and better.

From this point of view, much hidden work remains. How has this process happened? Although the computer is very powerful, you have to teach him how to do the work. For data to be outsourced, it is necessary to prepare it for complex treatments. In almost all fields of science, this laborious work is prepared by mathematicians and in measurements with oscillating data the Fourier transform is also used.

Earth Tremors

We will follow an example of what mathematician Joseph Fourier invented. Suppose a digital seismograph is launched in a territory where many earthquakes occur. This device constantly measures the movement of the soil, recording in every measure the displacement from the balance, detecting earthquakes by vibrations. Lower seismic waves should also be measured, allowing the frequency and intensity of activity to be known.

Suppose the seismograph receives 5 data in a second, then it will have to accumulate and process 432,000 daily numbers.

A succession of numbers is not very useful. The truth is that if depicted on a graph it looks better when earthquakes have occurred and whether they have been strong or not. However, the best thing to do operations and calculations is that the numbers are mathematical. This function indicates how the seismic wave amplitude has been modified over time, i.e., it is ultimately a continuous record of earth movements.

This is precisely the greatest difficulty: How can you get a function that fits well to thousands of points? Is it true that a single mathematical formula can represent any list of numbers received? When it comes to oscillatory measurements, it is obtained by transforming Fourier. The French mathematician devised a methodology to easily overcome this great difficulty.

Complex looking curves

The seismologist can draw the 432,000 points obtained throughout the day and, simply, intertwining, you will get a curve. But if that day there has been seismic activity, that curve will be very complex. (Of course, if there is no seismic activity all measurements will be zero and the work of the seismologist will not make sense). However, with such a complex curve, it is very difficult to calculate anything.

Fourier treatment is based on the decomposition of this complex curve. According to their theory, any function can be written as the sum of breasts and breasts of different frequency. What does that mean? According to this idea, instead of calculating the function, a sum of simple functions can be used. The image shows an example of this idea:

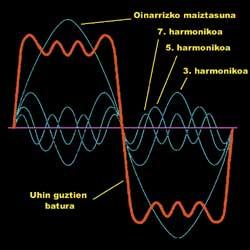
The complex function (red) is the sum of simple functions (blue). In the image there are only four functions attached, but if hundreds are used, the sum can be perfectly adjusted to the collected experimental data.

This methodology facilitates calculations but has other advantages, allows the analysis of the frequencies of the data. The terms of this sum, those "simple functions", are oscillating, but each of them is related to a frequency. The frequencies used in all terms are multiples of an initial one. It can be said that a simple function represents the contribution of a certain frequency in the general function to be sought. This is very useful for scientists.

For example, the seismologist can distinguish two seismic waves that have occurred simultaneously, since each one vibrates with its own frequency. It can also detect interference and negate the results of seismograph background noise.

Frequency space

Fourier analysis is equally useful in many other areas. Sound treatment is the clearest example. When the sound is recorded digitally, the background noise is originated by the recorder itself. Just looking for the "cleaning" frequency of that sound and removing this term from the function causes signal noise to be removed. In optics, for example, in photographic treatment.

The basic idea is therefore to break down a complex function into simple sinusoid functions. In the language of mathematicians, the function must be transformed from temporal space to frequency space. This means that, from the initial reference time, the set of selected frequencies is the same. The mathematical procedure for performing this step is the Fourier transform.

Mathematician and Egyptologist

If you look at the life of the French mathematician Jean Baptiste Joseph Fourier (1768-1830), XIX. The situation in Europe of the 20th century is reflected in the intense professional activity that it developed, especially in three areas. He always worked extensively in mathematics, politics and archaeology.

His fame as a mathematician is the XIX. from the beginning of the century. In order to study heat conduction in two-dimensional bodies, he developed a methodology with application in almost all areas of science. Currently this methodology is called Fourier transform. But he spent many years developing the transformed: It began in 1807 in Grenoble and ended in Paris in 1822.

He entered politics by the hand of the French Revolution. Napoleon participated in the expedition to Egypt, where he investigated the remains of the ancient civilization and, returning to France, summarized what he learned in the book Description of Egypt.

The scientific success of the Fourier era led him to become a member of the Academy of Science, the French Academy and the Academy of Medicine.

Applications...

Communications

In communications the signals are electrical, that is, simply pulses of tension. However, these signals travel through amplifiers, filters and communication channels, being able to alter these areas in many ways. Fourier transformation is essential to understand how these transformations occur. In short, these electrical signals are managed according to the frequencies. In the digital signal (composed of 0 and 1) it is also necessary to differentiate the frequencies. The voltage pulses of these signals must be adjusted to the bandwidth of the frequencies, using for this purpose the Fourier transform.

Seismology

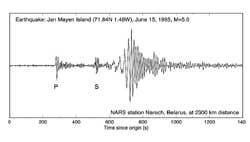
Seismic waves have their own frequencies. Its analysis allows to know the type and origin of the waves. This analysis is constantly used to investigate earthquakes and tectonic plates, but it is not the only application. Among other things, in the oil and gas industry much has been used to look for new sources. This type of research is used to differentiate natural seismic waves from those caused by a nuclear explosion. These separations depend on the frequencies, so Fourier transformation is essential in the mathematical treatment of the data.

Sonar

This technique is used to detect anything in the water. The basic operation is very simple: sound waves are emitted to the bottom and when it hits something, the wave bounces off (echo). The analysis of the intensity, frequency and reflection time of the reflected wave allows to know the situation and nature of the object. Frequency analysis is performed by Fourier transformation.

Spectroscopy

Spectroscopy is used to identify the chemical components of a substance; when energy is provided, each molecule has its own response. The molecule "absorbs" or releases a certain amount of energy by electromagnetic waves. The analysis of the frequencies of these waves allows the chemist to identify the molecules.

Acoustic

Sound is a mixture of many frequencies. The timbre of an instrument, for example, depends on the input of harmonics. Therefore, when sound becomes an electrical signal, Fourier analysis is essential in both digital and analog treatment. For example, equalization is acting with frequency intervals.

Astronomy

With the radio telescope you can see things that do not reflect lights. For example, the surface of Venus is surrounded by a dense layer of clouds. But astronomers have been able to explore its surface using radio waves. Moreover, in order to calculate the rotation period, we must take into account how these waves are reflected on the surface. These studies require a frequency analysis.

Optics

The Fourier transform produces in the light an effect similar to a prism: it separates the components it contains, that is, the light rays of different wavelength. However, this is done mathematically, meaning that the physical effects of light can be analyzed mathematically. For example, by passing through a slot, you can know the influence of diffraction in light. This analysis applied to visible light also serves any other wavelength: microwave, x-ray, infrared, etc.