Transformée de Fourier

2002/10/01 Roa Zubia, Guillermo - Elhuyar Zientzia Iturria: Elhuyar aldizkaria

• Matematika

Qu'y a-t-il derrière la chère équipe de scientifiques ? Comment traitez-vous les données que ces machines reçoivent ? En général, nous ne nous soucions pas beaucoup. Un ordinateur récupérera les mesures et reflétera les résultats par un graphique moderne. En outre, plus l'outillage est cher, plus précis et mieux.

De ce point de vue, il reste beaucoup de travail caché. Comment ce processus est-il arrivé ? Bien que l'ordinateur soit très puissant, il faut lui apprendre comment faire le travail. Pour que les données soient externalisées, il est nécessaire de les préparer à des traitements complexes. Dans presque tous les domaines de la science, ce travail laborieux est préparé par les mathématiciens et dans les mesures avec des données oscillantes est également utilisé la transformée de Fourier.

Tremblements de terre

Nous allons suivre un exemple de ce qu'a inventé le mathématicien Joseph Fourier. Supposons qu'un sismographe numérique est lancé sur un territoire où de nombreux tremblements de terre se produisent. Ce dispositif mesure constamment le mouvement du sol, enregistrant dans chaque mesure le déplacement depuis l'équilibre, en détectant les tremblements de terre par des vibrations. Les petites ondes sismiques doivent également être mesurées, ce qui permet de connaître la fréquence et l'intensité de l'activité.

Supposons que le sismographe reçoit 5 données en une seconde, alors il faudra accumuler et traiter 432.000 numéros par jour.

Une succession de nombres n'est pas très utile. La vérité est que si représenté sur un graphique, il semble mieux quand les tremblements de terre ont eu lieu et s'ils ont été forts ou non. Cependant, la meilleure chose à faire est que les nombres soient mathématiques. Cette fonction indique comment l'amplitude de l'onde sismique a été modifiée au fil du temps, c'est, en définitive, un enregistrement continu des mouvements de la terre.

En cela consiste précisément la plus grande difficulté: comment pouvez-vous obtenir une fonction qui correspond bien à des milliers de points? Est-il vrai qu'une seule formule mathématique peut représenter n'importe quelle liste de nombres reçue ? Quand il s'agit de mesures oscillantes, il est obtenu en transformant Fourier. Le mathématicien français a conçu une méthodologie pour surmonter facilement cette grande difficulté.

Courbes d'aspect complexe

Le sismologo peut dessiner les 432.000 points obtenus tout au long de la journée et, simplement en entrelacant, vous obtiendrez une courbe. Mais s'il y a eu une activité sismique ce jour-là, cette courbe sera très complexe. (Bien sûr, s'il n'y a pas d'activité sismique toutes les mesures seront zéro et le travail du sismologo n'aura pas de sens). Cependant, avec une courbe si complexe, il est très difficile de calculer quoi que ce soit.

Le traitement de Fourier est basé sur la décomposition de cette courbe complexe. Selon sa théorie, toute fonction peut être écrite comme la somme des seins et des cosinus de fréquence différente. Que signifie cela ? Selon cette idée, au lieu de calculer la fonction, vous pouvez utiliser une somme de fonctions simples. L'image montre un exemple de cette idée:

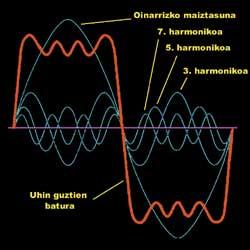
La fonction complexe (rouge) est la somme des fonctions simples (bleues). Sur l'image, il n'y a que quatre fonctions jointes, mais si des centaines sont utilisées, la somme peut être parfaitement ajustée aux données expérimentales recueillies.

Cette méthodologie facilite les calculs mais a d'autres avantages, permet l'analyse des fréquences des données. Les termes de cette somme, ces "fonctions simples", sont oscillants, mais chacun d'eux est lié à une fréquence. Les fréquences utilisées dans tous les termes sont des multiples d'un initial. On peut dire qu'une fonction simple représente la contribution d'une certaine fréquence dans la fonction générale à rechercher. Ceci est très utile pour les scientifiques.

Par exemple, le sismologo peut distinguer deux ondes sismiques qui se sont produites simultanément, car chacune vibre avec une fréquence propre. Il peut également détecter les interférences et mépriser les résultats du bruit de fond du sismographe.

Espace de fréquence

L'analyse de Fourier est également utile dans de nombreux autres domaines. Le traitement du son est l'exemple le plus clair. Lorsque le son est enregistré numériquement, le bruit de fond est généré par le graveur lui-même. Le simple fait de rechercher la fréquence de "nettoyage" de ce son et d'éliminer ce terme de la fonction fait disparaître le bruit du signal. En optique, par exemple, dans le traitement photographique.

L'idée de base est donc de décomposer une fonction complexe en fonctions simples sinusoïdes. Dans le langage des mathématiciens, la fonction doit être transformée de l'espace temporel à l'espace de fréquence. Cela signifie que, à partir du temps de référence initial, l'ensemble des fréquences sélectionnées est le même. La procédure mathématique pour effectuer cette étape est le transformé de Fourier.

Mathématicien et égyptologue

Si vous regardez la vie du mathématicien français Jean-Baptiste Joseph Fourier (1768-1830), XIX. La situation de l'Europe du XXe siècle se reflète dans l'intense activité professionnelle qu'elle a développée, surtout dans trois domaines. Il a toujours exercé une grande activité en mathématiques, politique et archéologie.

Sa réputation de mathématicien est le XIX. depuis le début du siècle. Afin d'étudier la conduction de chaleur dans des corps bidimensionnels, il a développé une méthodologie appliquée dans presque tous les domaines de la science. Actuellement cette méthodologie est appelée transformée de Fourier. Mais il a consacré de nombreuses années à développer ce qui a été transformé: Il a commencé en 1807 à Grenoble et a terminé à Paris en 1822.

Il est entré en politique de la main de la Révolution française. Napoléon a participé à l'expédition en Egypte, où il a enquêté sur les restes de l'ancienne civilisation et, de retour en France, a résumé ce qu'il a appris dans le livre Description de l'Egypte.

Le succès scientifique de l'époque Fourier l'a amené à devenir membre de l'Académie des sciences, de l'Académie française et de l'Académie de médecine.

Applications ...

Communications

Dans les communications, les signaux sont électriques, c'est-à-dire simplement des impulsions de tension. Cependant, ces signaux traversent des amplificateurs, des filtres et des canaux de communication, pouvant modifier ces zones de plusieurs façons. La transformation de Fourier est indispensable pour comprendre comment ces transformations se produisent. En définitive, ces signaux électriques sont gérés en fonction des fréquences. Dans le signal numérique (composé de 0 et 1) il est également nécessaire de différencier les fréquences. Les impulsions de tension de ces signaux doivent être ajustées à la bande passante des fréquences, en utilisant pour cela la transformée de Fourier.

Sismologie

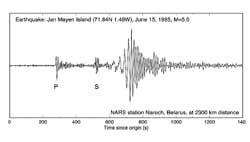
Les ondes sismiques ont leurs propres fréquences. Son analyse permet de connaître le type et l'origine des ondes. Cette analyse est constamment utilisée pour rechercher des tremblements de terre et des plaques tectoniques, mais ce n'est pas la seule application. Entre autres choses, l'industrie pétrolière et gazière a beaucoup été utilisée pour rechercher de nouvelles sources. Ce type de recherche est utilisé pour différencier les ondes sismiques naturelles de celles provoquées par une explosion nucléaire. Ces séparations dépendent des fréquences, de sorte que la transformation de Fourier est indispensable dans le traitement mathématique des données.

Sonar

Cette technique sert à détecter tout dans l'eau. Le fonctionnement de base est très simple : des ondes sonores sont émises vers le fond et lorsque l'onde rebondit (écho). L'analyse de l'intensité, de la fréquence et du temps de réflexion de l'onde réfléchie permet de connaître la situation et la nature de l'objet. L'analyse des fréquences est effectuée par la transformation de Fourier.

Spectroscopie

La spectroscopie est utilisée pour identifier les composants chimiques d'une substance ; quand l'énergie est fournie, chaque molécule a sa propre réponse. La molécule "absorbe" ou libère une certaine quantité d'énergie par des ondes électromagnétiques. L'analyse des fréquences de ces ondes permet au chimiste d'identifier les molécules.

Acoustique

Le son est un mélange de nombreuses fréquences. Le timbre d'un instrument, par exemple, dépend des apports des harmoniques. Ainsi, lorsque le son devient signal électrique, l'analyse de Fourier est indispensable aussi bien dans le traitement numérique qu'analogique. Par exemple, l'égalisation est d'agir avec des intervalles de fréquence.

Astronomie

Avec le radiotélescope, vous pouvez voir des choses qui ne reflètent pas les lumières. Par exemple, la surface de Vénus est entourée d'une couche dense de nuages. Mais les astronomes ont pu explorer leur surface par des ondes radio. De plus, pour calculer la période de rotation, il faut tenir compte de la façon dont ces ondes se reflètent sur la surface. Ces études nécessitent une analyse des fréquences.

Optique optique optique

La transformée de Fourier produit dans la lumière un effet similaire à un prisme : elle sépare les composants qu'elle contient, c'est-à-dire les rayons lumineux de différentes longueurs d'onde. Cependant, cela se fait mathématiquement, ce qui signifie que les effets physiques de la lumière peuvent être analysés mathématiquement. Par exemple, en passant par une fente, vous pouvez connaître l'influence de la diffraction dans la lumière. Cette analyse appliquée à la lumière visible sert également à toute autre longueur d'onde : micro-ondes, rayons X, infrarouges, etc.