Funtzio jarraitu baina ez-deribagarriak: bitxikeria matematikoa ala errealitatearen isla?

Analisi matematikoa matematikaren alor nagusi bat da, oinarri-oinarrian zenbakiak eta haien arteko erlazioak aztertzen dituena. Erlazio horien artean garrantzi handikoak dira funtzioak. Zenbakiak aski ezagunak zaizkigu, baina zer da funtzio bat? Bada, arau bat besterik ez da, zenbaki bati beste zenbaki bat esleitzen diona. Kontzeptu erraza den arren, matematikaren eta zientziaren funtsezko tresna dira. Satelite baten abiadura, gaixotasun batek kutsatutako pertsona-kopurua, burtsaren gorabeherak, bihar izango dugun tenperatura… Oro har, funtzio baten bidez adierazten da zenbakizko balioa duen edozein aldagai.

1. irudia: Funtzio orokor baten grafoa. Arg. Daniel Eceizabarrena

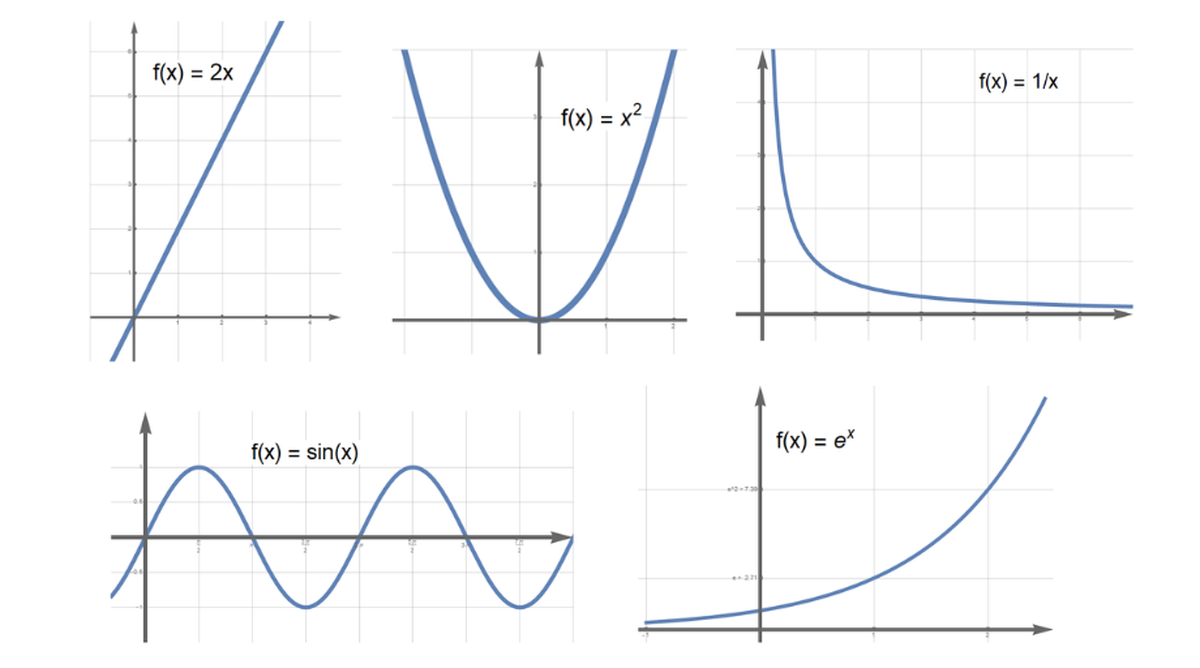
Ohikoena da funtzio orokor bati \(f\) deitzea, eta funtzio horrek \(x\) edozein zenbakiri \(f(x)\) beste zenbaki bat esleitzen dio. Adibide bat jartzearren, demagun  \(f(x) = 2x\) dela. Funtzio horrek edozein zenbakiri bere bikoitza esleitzen dio: \(x = 1\)  zenbakiari \(f(1) = 2\) , eta \(x=5\)  zenbakiari, berriz, \(f(5)=10\) . Era berean defini ditzakegu \(f(x)=x^2\)  karratua, \(f(x)=1/x\)  alderantzizkoa, \(f(x)=\sin⁡(x)\)  sinua edota \(f(x) = e^x\) esponentziala. Funtzio horiek oso ohikoak eta erabilgarriak dira. Adibidez, soinu- eta irrati-uhinek sinu-itxura daukate, eta populazioen hazkundea esponentziala izaten da. Funtzio horiek propietate matematiko itzelak dituzte: jarraituak dira eta nahi bezain beste aldiz deriba daitezke.

Funtzioak irudikatzen: grafoak

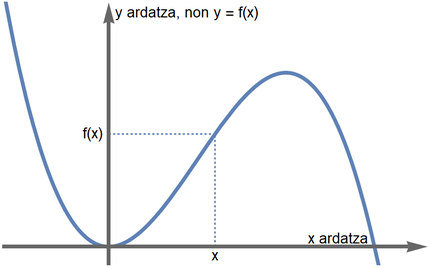
Propietate horietaz jabetzeko modu sinple bat funtzioak irudikatzea da, eta hori grafoaren bidez egiten da (ikusi 1. irudia). Planoan \(x\)  eta \(y\)  ardatz perpendikularrak marrazten dira, eta \(y=f(x)\)  ezarriz, \((x,f(x))\)  koordenatuak dituzten puntuak marrazten dira. Emaitza kurba bat da, eta funtzio bakoitzari kurba ezberdin bat dagokio. 2. irudian ageri denez, \(f(x)=2x\)  funtzioari lerro zuzen bat dagokio, \(f(x)=x^2\)  parabola bat da eta \(f(x)=1/x\)  hiperbola bat.

2. irudia: Oinarrizko zenbait funtzioren grafoak. Arg. Daniel Eceizabarrena

3. irudia: Funtzio honek etengunea du x₀ puntuan. Etena da. Arg. Daniel Eceizabarrena

Funtzio baten grafoak argi erakusten ditu funtzioaren propietate batzuk. Funtzio bat jarraitua da marraztutako kurbak etenik ez badu. Funtzio horien balioak saltorik gabe aldatzen dira. Adibidez, 2. irudiko funtzioak jarraituak dira. Bestela, funtzioa etena dela esaten da (ikusi 3. irudia).

4. irudia: Funtzio hau ez da deribagarria x₁ eta x₂ puntuetan, izkinak dituelako. Arg. Daniel Eceizabarrena

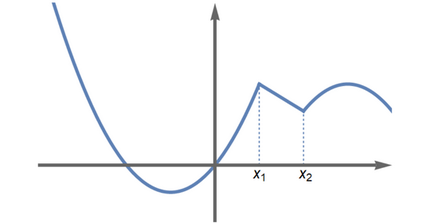
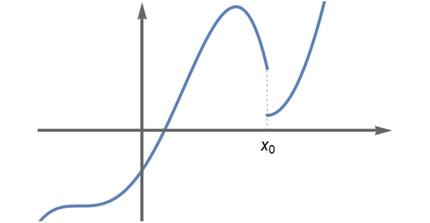
Funtzioen beste propietate garrantzitsu bat deribagarritasuna da. Funtzioa deribagarria (edo diferentziagarria) da bere grafoak itxura leuna badauka, izkinarik ez badu. Funtzio horien balioek ez dute joera-aldaketa bortitzik. Adibidez, 2. irudiko grafoak leunak dira eta funtzio deribagarriei dagozkie, baina 4. irudiko grafoak bi izkina dauzka, eta, beraz, funtzio hori ez da deribagarria.

5. irudia: Funtzio hau jarraitua da x₁ puntuan izan ezik, eta deribagarria da x₁ eta x₂ puntuetan izan ezik. Arg. Daniel Eceizabarrena

6. irudia: Hainbat izkina dituen funtzio jarraitua. Izkinak dituen puntuetan, funtzioa ez da deribagarria. Arg. Daniel Eceizabarrena

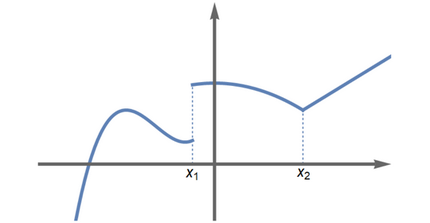
Askotan, era globalean baino, funtzio baten jarraitutasuna eta deribagarritasuna puntuka edo tarteka aztertzen da. Izan ere, funtzio bat jarraitua edo deribagarria izan daiteke puntu batzuetan eta beste batzuetan ez, 5. irudian ageri den bezala.

Bi propietate horiek oinarri-oinarrizko erlazio batek lotzen ditu; izan ere, funtzio deribagarri bat beti da jarraitua. Noski, leuna den kurba batek ez du saltorik, salto batek leuntasuna apurtuko luke eta! Baina zer esan kontrakoari buruz? Funtzio jarraituak deribagarriak al dira nahitaez?

Funtzio jarraitu baina ez-deribagarriak

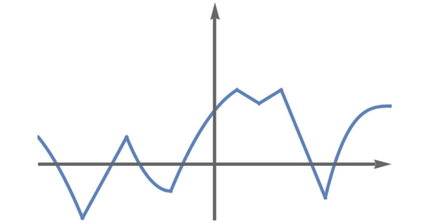
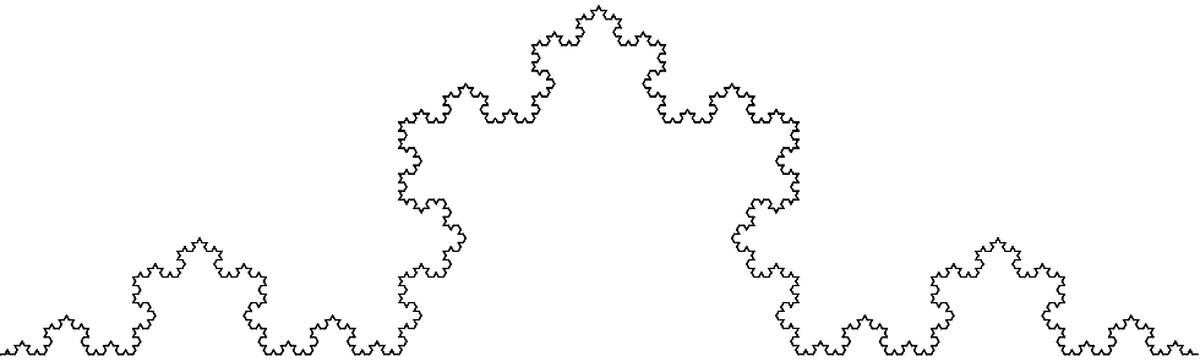
Erantzuna ezezkoa da, jakina. Funtzioa jarraitua izan daiteke deribagarria izan gabe, grafo jarraitu batek izkinak izan ditzake-eta. 4. irudian dugu horren adibide bat. Are gehiago, erraz marraz dezakegu nahi bezain beste izkina dituen kurba bat, 6. irudian ageri den bezala.

Gehixeago egiten saiatuko gara. Posible al da kurba jarraitu batek izkinak izatea puntu guzti-guztietan? Intuizioak, edo eskuz saiatze hutsak, ezezkoa dio. Baina, hori bai galdera bitxia! Zentzurik ba al duen pentsatuko du batek baino gehiagok. Hara non, XIX. mendeko matematikarien buruhauste nagusienetariko bat izan zen hori. Garai hartan, matematikaren oinarri teorikoak guztiz ezarri gabe zeuden oraindik, eta kontzeptuak kontu handiz definitu behar zituzten kontraesanik ez sortzeko. Galdera horri dagokionez, gehienek pentsatzen zuten ezinezkoa zela horrelako grafoa egitea. Lengoaia matematikoan esanda, ezin zela sortu inon deribagarria ez zen funtzio jarraiturik.

Usteak erdia ustel. Karl Weierstrassen esanetan [W], 1860ko hamarkadan, Bernhard Riemannek funtzio jarraitu exotiko bat proposatu zuen eta esan zuen deribaturik ez zuela inon. Funtzioak honako itxura hau du:

 \(f(x)= \displaystyle\sum_{n=1}^{∞} \frac{\sin (n^2 x)}{n^2} =\sin⁡(x)+ \frac{\sin⁡(4x)}{4}+\frac{\sin⁡(9x)}{9}+\frac{\sin⁡(16x)}{16}+⋯\)

7. irudia. Riemannen funtzio ez-diferentziagarriaren grafoa. Arg. Daniel Eceizabarrena

Ados, hasierakoak baino korapilatsuagoa da. Baina propietate arraroak dituen funtzioa bera ere ez al da arraroa izango? Hasteko, batuketa infinitu horren emaitza beti da zenbaki finitu bat, x  edozein delarik ere. Izan ere, edozein zenbakiren sinua beti da 1 baino txikiagoa, eta Leonhard Eulerrek 1735ean frogatu zuen karratuen alderantzizkoen baturaren emaitza \(1+\frac{1}{4}+\frac{1}{9}+\frac{1}{16}+⋯=\frac{π^2}{6}\)  dela. Funtzioaren jarraitutasuna ere ez zen frogatzeko zaila. Deribagarritasunari dagokionez, ordea, inork ez zuen Riemannek esandakoa frogatzerik lortu. Misterio hutsa izan zen 1970era arte [G].

8. irudia: 7. irudiko bi zati handituta ageri dira hemen, izkinaz beteta dagoela ikusteko. Oso bitxia da eskuineko irudiaren erdian, (1,0) puntuan, agertzen den puntu leuna. Arg. Daniel Eceizabarrena

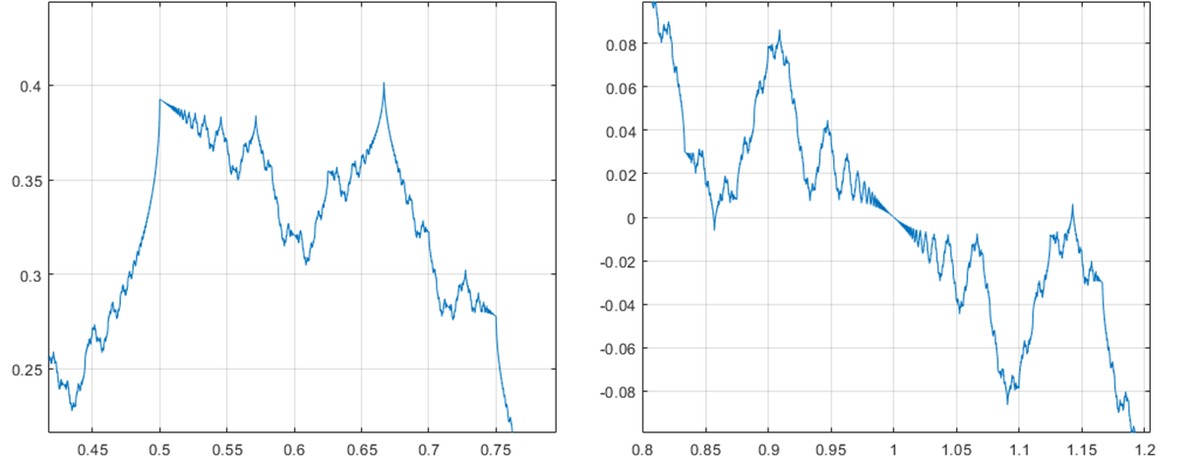
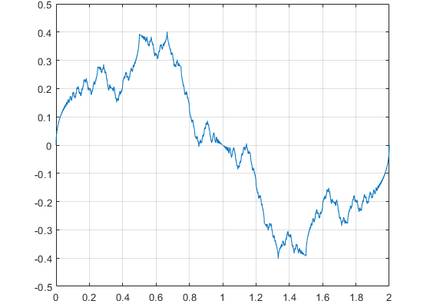
Ehun urte, alajaina! Funtzio hori ez da ahuntzaren gauerdiko eztula. Riemannen funtzio ez-diferentziagarria da haren izena, eta, imajinatuko duzuenez, ia ezinezkoa da haren grafoa eskuz marraztea. Eskerrak ordenagailuak eskura dauzkagun! Ikusi 7. eta 8. irudiak. Bitxia benetan. Guztiz zuzen esateko, Riemannen funtzioak ez du deribaturik ia inon, grafoaren erdialdean, (1,0)  koordenatuan, lerro zuzen bat sortzen baita. Hor funtzioak deribatua du, baina beste inon ez.

9. irudia: Kochen kurba edo elur-maluta, kurba jarraitu eta ez-diferentziagarria. Lehenetariko fraktal baten adibidea dugu hauxe. Arg. Daniel Eceizabarrena

10.irudia: Higidura browndarra edo Wienerren prozesua. Polen-partikulen higidura deskribatzeko proposatu zuten, baina gaur egun hainbat molekularen higidura ulertzeko erabiltzen da. Arg. Daniel Eceizabarrena

Riemannen funtzioak hasiera eman zion funtzio jarraitu eta ez-deribagarrien lasterketari. Asko proposatu zituzten, baina matematikari asko haien kontra agertu ziren, zentzurik ez zutela esanez. Henri Poincarék, adibidez, hauxe esan zuen: “Badirudi funtzio horien xedea dela zerbaiterako balio duten funtzioen ahalik eta antz gutxien izatea” [P]. Baina geroz eta adibide gehiago sortzen ari ziren, eta bereziki higidura browndarraren garapenaren ostean, funtzio jarraitu eta ez-deribagarriak guztiz onartuak izan ziren. Gero, 1970eko hamarkadan, Benoît Mandelbrotek fraktalak proposatu zituen funtzio horiek guztiak bateratzeko asmoz, gertaera naturalak deskribatzeko lagungarriak izan zitezkeelakoan. Izan ere, haren hitzetan, “lainoak ez dira esferak, mendiak ez dira konoak, kostaldeak ez dira zirkuluak eta zuhaitzen azala ez da leuna. Tximistak ere ez dira lerro zuzenean hedatzen” [M, 1. orr.]. Ez zaio arrazoirik falta.

Riemannen funtzioa naturan

Egia esan, era fisikoan agertzen dena Riemannen funtzioaren bertsio bat da, hauxe:

\(f(x)=ix+\displaystyle\sum_{n=1}^{∞} \frac{e^{in^2 x}}{n^2} =ix+\displaystyle\sum_{n=1}^{∞} \frac{\cos⁡(n^2 x) }{n^2} +i \displaystyle\sum_{n=1}^{∞} \frac{\sin⁡(n^2 x)}{n^2} .\)

11. irudia: Riemannen funtzio ez-diferentziagarriaren aldaera konplexuaren irudikapena. Honek ere izkinak ditu nonahi. Arg. Daniel Eceizabarrena

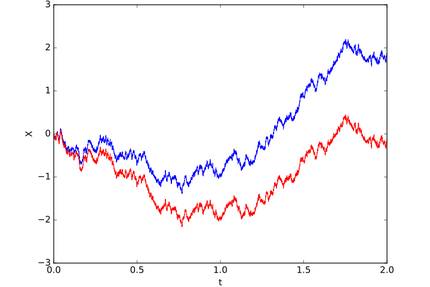
Adierazpen horretan zenbaki konplexuak ageri dira, \(i = \sqrt{-1}\)  unitate konplexuarekin sortzen direnak. Gaurkoan ez gara haiei buruz arituko, baina argi dago funtzio berri horrek Riemannen funtzio ez-diferentziagarriaren egitura matematiko berbera duela. Haren irudikapena 11. irudian ageri da.

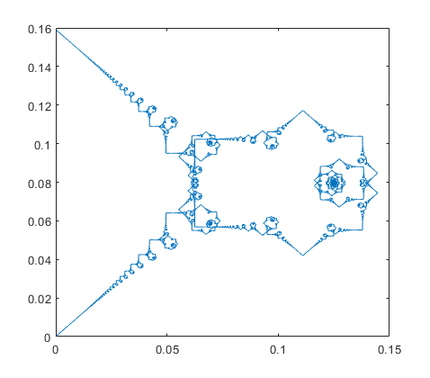
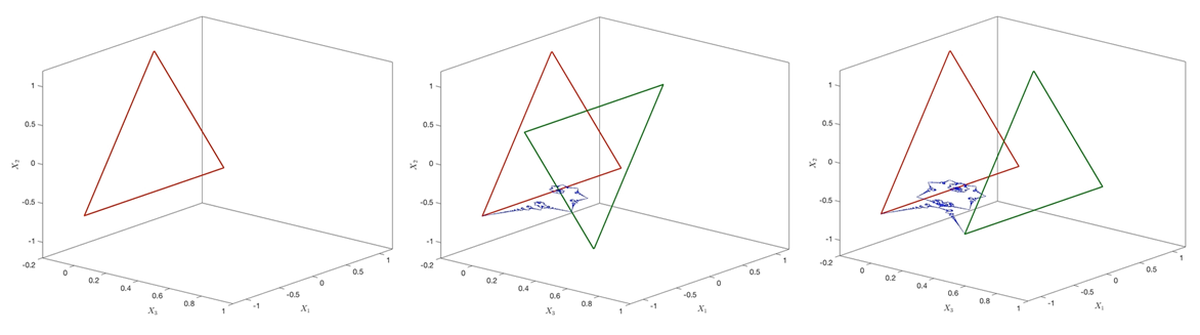
Modu harrigarrian, De la Hoz eta Vega EHUko irakasleek erakutsi zuten funtzio hori ke-eraztunen mugimenduan agertzen dela [H-V]. Denok dakigu ke-eraztunak nola hedatzen diren: erretzaile batek horrelako bat sortzen duenean, keak zirkulu-itxura mantentzen du bidaiatzen duen bitartean, hasieran behintzat. Baina zer gertatzen da eraztunak triangelu- edo lauki-itxura badu? Ez da egoera arraroa, industrian tutu triangeluar eta karratuak erabiltzen baitira. Esperimentu horixe egin zuten Kleckner, Scheeler eta Irvinek hirusta-itxurako eraztun batekin [K-S-I]. Oso gomendagarria da haien artikuluko bideoa ikustea, bertan erakusten duten emaitza ikusgarria baita: hirusta buruz behera jartzen da lehenbizi, gero berriro buruz gora, eta horrela etengabe. 12. Irudian, triangeluari dagokion simulazio matematikoa ageri da, eta benetako esperimentuan hirustari gertatzen zaion berbera gertatzen zaio. Simulazio horren bideoa https://sites.google.com/view/skumar1712/simulation-videos web-orrian dago ikusgai [K].

12. irudian bertan, urdinez marraztuta triangeluaren izkina baten ibilbidea ageri da. 11. irudiko kurbarekin konparatuz, Riemannen funtzioaren izugarrizko antza dauka! Horrek erakusten du Riemannen funtzioak berezko egitura fisiko eta geometrikoa daukala, esperimentu natural batean agertzen baita.

12. irudia: Ke-eraztun triangeluarraren bilakaera. Urdinez, triangeluaren izkina baten ibilbidea. Irudia: Sandeep Kumar, BCAM. Haren baimenarekin. Arg. Daniel Eceizabarrena

Riemannen funtzioaren azterketa geometrikoa

Riemannen funtzioak ibilbide fisiko bat adierazten duenez, garrantzizkoa da haren propietate geometriko eta fisikoak aztertzea. Horixe izan da nire doktorego-tesiaren ardatza [E1]. Aztertutako galderen artean, honako hau nabarmenduko nuke: ibilbide hori jarraitzen duen partikula bat hartuz gero, posible al da puntu guztietan partikularen abiadura eta norabidea kalkulatzea? Emaitza ezezkoa da, Riemannen funtzioa deribagarria ez izatearen  ondorioz [E2]. Baina, bestalde, partikula mugitu egiten da batez besteko abiadura eta norabide batekin. Harrigarria, ezta? Beste emaitza batzuk aipatzearren, ibilbidearen Hausdorffen dimentsioa 4/3 izateko aukerak handiak dira [E3], eta, gainera, turbulentziaren teoriaren aldetik, ibilbidea intermitentea da [B-E-V].

Riemannen funtzioari, funtzio ez-deribagarriei eta, oro har, fraktalei buruz egin daitekeen galdera matematiko mordoa dago, eta denek potentzial handia dute gertaera naturalak deskribatzeko. Horra hor askotan misteriotsua eta ezezaguna den matematikari teoriko askoren lanaren adibide bikaina!

BIBLIOGRAFIA

[B-E-V] A. Boritchev, D. Eceizabarrena, V. Vilaça da Rocha. Intermittency of Riemann's non-differentiable function thought the fourth-order flatness. J. Math. Phys. 62 (2021), 093101. https://doi.org/10.1063/5.0011569

[E1] D. Eceizabarrena. A geometric and physical study of Riemann’s non-differentiable function. Doktorego tesia (2020), Euskal Herriko Unibertsitatea (UPV/EHU). https://addi.ehu.es/handle/10810/49901

[E2] D. Eceizabarrena. Geometric differentiability of Riemann’s non-differentiable function. Adv. Math. 366 (2020), 107091. https://doi.org/10.1016/j.aim.2020.107091

[E3] D. Eceizabarrena. On the Hausdorff dimension of Riemann's non-differentiable function. Trans. Amer. Math. Soc. 374 (2021), 7679-771. https://doi.org/10.1090/tran/8489 

[G] J. Gerver. The differentiability of the Riemann function at certain rational multiples of π . Amer. J. Math. 92 (1970), 33-55. https://doi.org/10.2307/2373496                      

[H-V] F. de la Hoz, L. Vega. Vortex filament equation for a regular polygon. Nonlinearity 27 (2014), 3031–3057. https://doi.org/10.1088/0951-7715/27/12/3031

[K-S-I] D. Kleckner, M. W. Scheeler, W. T. M. Irvine. The life of a vortex knot. Phys. Fluids 26 (2014), 091105. https://doi.org/10.1063/1.4893590

[K] S. Kumar. Web orria. https://sites.google.com/view/skumar1712/simulation-videos

[M] B. Mandelbrot. The fractal geometry of nature. W. H. Freeman and Co., San Francisco, Calif., 1982.

[P] H. Poincaré. La logique et l’intuition dans la science mathématique et l’enseignement. Enseign. Math. 1 (1899), 157-162. https://www.e-periodica.ch/digbib/view?pid=ens-001:1899:1#309

[W] Karl Weierstrass. Über continuirliche Functionen eines reellen Arguments, die für keinen Werth des letzteren einen bestimmten Differentialquotienten besitzen. Mathematische Werke. II. Abhandlungen 2. 1895, 71-74.