}

Geneak, neuronak eta ordenagailuak

2015/01/01 Azkune Galparsoro, Gorka - Ikertzailea eta irakasleaEuskal Herriko Unibertsitateko Informatika Fakultatea Iturria: Elhuyar aldizkaria

Pentsatzea eta ikastea. Gizakion bi ezaugarri nabarmendu nahiko bagenitu, agian horiexek izango lirateke gehienon ahotan. Harrigarria baita ume jaioberri batek, denboraren poderioz eta bere garunaren ahalmenaz, ikaskuntza-prozesu jarraitu horrekin zer bilakaera lor dezakeen. Gaur egun, hala ere, bi ezaugarri horiek makinetan ere presente daude. Adimen artifizialari esker, gure makinak gero eta adimendunagoak dira eta ikasteko gaitasuna dute. Baina nola egiten dute hori?
geneak-neuronak-eta-ordenagailuak
Arg. computerworld.hu

Natura inspirazio-iturri

Adimen artifizialaren kontzeptua XX. mendearen erdialdearen inguruan agertu zen gure artean. Hastapenetan, adimen sinbolikoarekin eta bilatzeari lotutako arazoekin hasi ziren lanean. Adibide ona izan ziren xake-jokalari artifizialak. IBMren Deep Blue ordenagailu ospetsuak lortu zuen arrakastarik handiena, Gary Kasparov xake-jokalari ospetsua menderatu baitzuen 1997. urtean.

Makina haiek, hala ere, ez ziren gizakiaren adimenaren parekoak. Gauza zehatz bat oso ongi egiteko gai ziren; baina ez besterik. Ez zuten ikasten, ez ziren gai beren ezagutza orokortzeko eta, jokoaren arauak pixka bat aldatuz gero, ezin zuten erreakzionatu. Hori zela eta, ikertzaileek bide berriak jorratu zituzten, eta adimen artifizialaren esparru berri bat landu zuten: ikaskuntza automatikoa.

Artikulu honetan, ez dugu bere osotasunean aztertuko ikaskuntza automatikoa. Arlo zehatz baina erakargarri batean sartuko gara: naturan inspiratutako algoritmoak eta ikaskuntza. Gizakion ikasteko moduaren antz handia duen prozesu batera hurbilduko gara, sare neuronalak eta algoritmo genetikoak konbinatuz.

Sare neuronalak

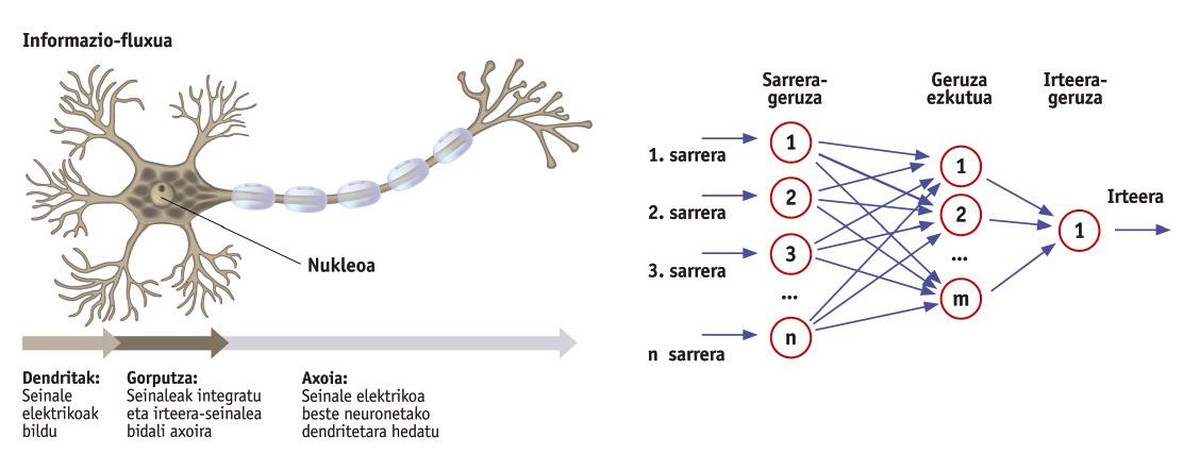
Gure garuna neuronaz osatua dago, elkarrekin konektaturiko neurona-pila batez. Baina neurona horietako bat bakarra aztertuz gero, harrituta utziko gaitu haren sinpletasunak. Informazioaren ikuspegitik, neuronek sarrera-datu batzuk jasotzen dituzte seinale elektriko moduan, eta beste seinale bat kanporatzen dute (1. irudia). Beraz, gure garunaren prozesatzeko gaitasuna neurona sinple horien elkarrekintzan datza.

Ideia hori buruan, ez dirudi oso zaila sare neuronal artifizialak egiteak. Eta ez da zaila. Aurreko mendeko 40ko eta 60ko hamarkaden artean garatu ziren lehen sare neuronal artifizialak. Hala ere, haien ahalmena ez zen agerian geratu 80ko hamarkadaren bukaerara arte. Gaur egun, sare neuronalak hamaika aplikaziotan aurkitu daitezke.

Sare neuronalak datu-sarrera batzuk datu-irteera bihurtzen dituzten neurona-multzo bat baino ez dira. 2. irudian ikus daitekeenez, sare neuronalak geruzatan antolatzen dira: sarrera-geruza, geruza ezkutua (nahi adina geruza ezkutu jar daitezke) eta irteera-geruza. Geruza bakoitza neuronaz osaturik dago (irudiko biribiltxoak), eta geruza bateko neurona guztiak hurrengo geruzako neuronekin konektatuta egoten dira. Horrelakoa da sare neuronal arrunt baten egitura. Kontu izan mota askotako sareak egon daitezkeela, helburu ezberdinak betetzeko. Adibidez, sare batzuek irteera-geruzako neuronak geruza ezkutuko neuronekin konektatzen dituzte, sareak memoria izan dezan. Baina, oraingoz, egitura konplexuak alde batera utziko ditugu.

Neurona bakoitzaren sarrerak zenbakiak dira. Zenbaki horiek neurona batera iristen direnean, pisu deritzen beste zenbaki batzuez biderkatzen dira, eta, ondoren, emaitza guztiak batzen dira. Batura hori izango da neuronaren irteera. Ikusten den bezala, neurona bakoitzak egiten duena oso sinplea da. Baina sare osoa, neurona guztiak konektatuta, edozein funtzio matematiko inplementatzeko gai da. Horra hor sarearen boterea. Esan berri duguna matematikoki froga daiteke, baina hori artikulu honen helburuetatik at dago.

Neurona bateko informazio-fluxua (1. irudia. Irudigilea: alila/123RF) eta sare neuronal tipiko bat (2. irudia). Datu-sarrera batzuk datu-irteera bihurtzen dituzten neurona-multzo bat baino ez dira sare neuronalak.

Beraz, sare neuronal baten portaeran, berebiziko garrantzia dute haren egiturak (zenbat geruza dituen eta konexioen izaera) eta neurona bakoitzaren pisuak. Eragiketa sinpleak egiteko, nahikoa da sare txiki bat, eta, kasu horretan, erraz finkatzen dira pisu guztiak eta zehazten da egitura egokia. Baina aplikazio konplexuek sare handiak behar izaten dituzte, eta, sare handi horietan, ia ezinezkoa da neurona bakoitzaren pisu guztiak eskuz zehaztea. Horregatik, ezinbestekoa da sare neuronalak berak ezartzea pisu horien balioak, prozesu automatiko baten bidez. Prozesu horri ikaskuntza automatikoa deritzo, eta era askotara gauzatu daiteke. Guk hemen errefortzu bidezko ikaskuntza ikusiko dugu. Horretarako, ordea, lehenik eta behin, algoritmo genetikoak aztertu behar ditugu.

Algoritmo genetikoak

Darwinen eboluzioaren teoriak erakutsi zigun nola gertatzen den izaki bizidunen bilakaera. Ingurumenera ongien egokitzen direnak izaten dute ernaltzeko aukera gehien, eta, ernalkuntzaren ondorioz, gurasoen ezaugarriak konbinatzen dira eta bidea irekitzen zaio belaunaldi berriari. Ongien egokitzen diren indibiduoen ezaugarrien konbinaketaren bidez, belaunaldiz belaunaldi, indibiduo hobeak jaiotzen dira. Algoritmo genetikoek ideia horiek erabiltzen dituzte problema konplexuak optimizatzeko.

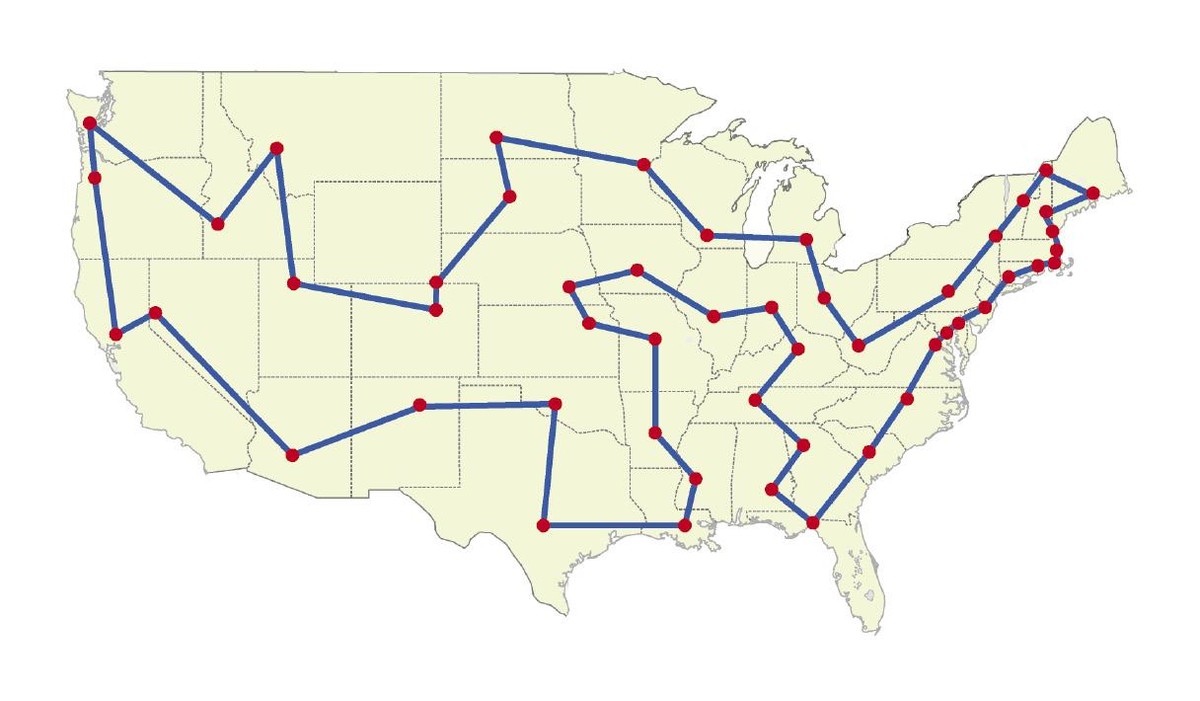
Azter dezagun problema hau. Bidaiari batek n hiri bisitatu nahi ditu, baina ez edonola. Dirua aurrezteko, n hiri horietatik pasatzen den biderik laburrena egin nahi du (3. irudia). Kontuan hartuta badakigula zein diren hiri guztien arteko distantziak, nola planifika dezakegu bidaia? Erraza dirudi: kalkula ditzagun hirien bisita-ordena guztiak, batu ditzagun distantziak eta har dezagun txikiena. Soluzio hori zuzena da; baina, n hiri-kopurua handia denean, ordenagailu batek denbora ikaragarri behar du soluzioa aurkitzeko. Beraz, ez da soluzio praktikoa.

Algoritmo genetikoek lan ona egin dezakete bidaiariaren problemarekin. Nola? Lehenik eta behin, hasierako belaunaldia sortzen da, eta n hirien ausazko konbinaketa batzuk sortzen dira. Ausazko konbinaketa horiei indibiduo deritze. Indibiduo bakoitzak ematen duen distantzia kalkulatzen da, eta distantzia txikienak ematen dituzten gutxi batzuekin geratzen da algoritmoa, elkarrekin gurutzatzeko. Hirien kasuan, adibidez, indibiduo baten lehen n/2 hiriak bigarrenaren n/2 hiriekin konbina ditzakegu, eta n hiriko beste indibiduo bat sortu. Gurutzaketen ondorioz sortzen diren indibiduoek bigarren belaunaldia eratzen dute.

3. irudia. AEBko bidaiariaren problema, eta soluzio posible bat. Azter dezagun problema hau. Bidaiari batek n hiri bisitatu nahi ditu, baina ez edonola. Dirua aurrezteko, n hiri horietatik pasatzen den biderik laburrena egin nahi du. Kontuan hartuta badakigula zein diren hiri guztien arteko distantziak, nola planifika dezakegu bidaia?

Bada, ordea, beste faktore garrantzitsu bat: mutazioa. Naturan bezalatsu, indibiduo berriak mutazioekin jaio daitezke. Gure kasuan, ausazko posizioetan dauden bi hiri elkarrekin trukatzea mutazio baten parekoa izan daiteke. Mutazioa gutxitan gertatzen da, baina oso funtzio garrantzitsua du indibiduo egokiagoak topatzeko.

Algoritmoak belaunaldi berriak sortzen dituen heinean, indibiduoek soluzio hobeak ematen dituzte. Azkenean, nahiz eta beti ez den posible izaten soluzio optimoa aurkitzea, optimotik oso gertu geratzen da indibiduo onena. Beraz, denbora gutxian oso soluzio ona aurkitu dezake. Ez al da harrigarria?

Errefortzu bidezko ikaskuntza

Orain dator politena. Demagun edozein norabidetan mugi daitekeen robot bat dugula. Guk erakutsi nahi diogu “eskuin” esaten dugunean eskuinera joaten eta “ezker” esaten dugunean ezkerrera mugitzen. Horretarako, mikrofono bat jarriko diogu, gure ahotsa hauteman dezan. Mikrofonoak sortzen duen seinalea sare neuronal baten sarrera izango da. Irteera, berriz, robota mugitzeko balio duten motorren seinaleak (4. irudia).

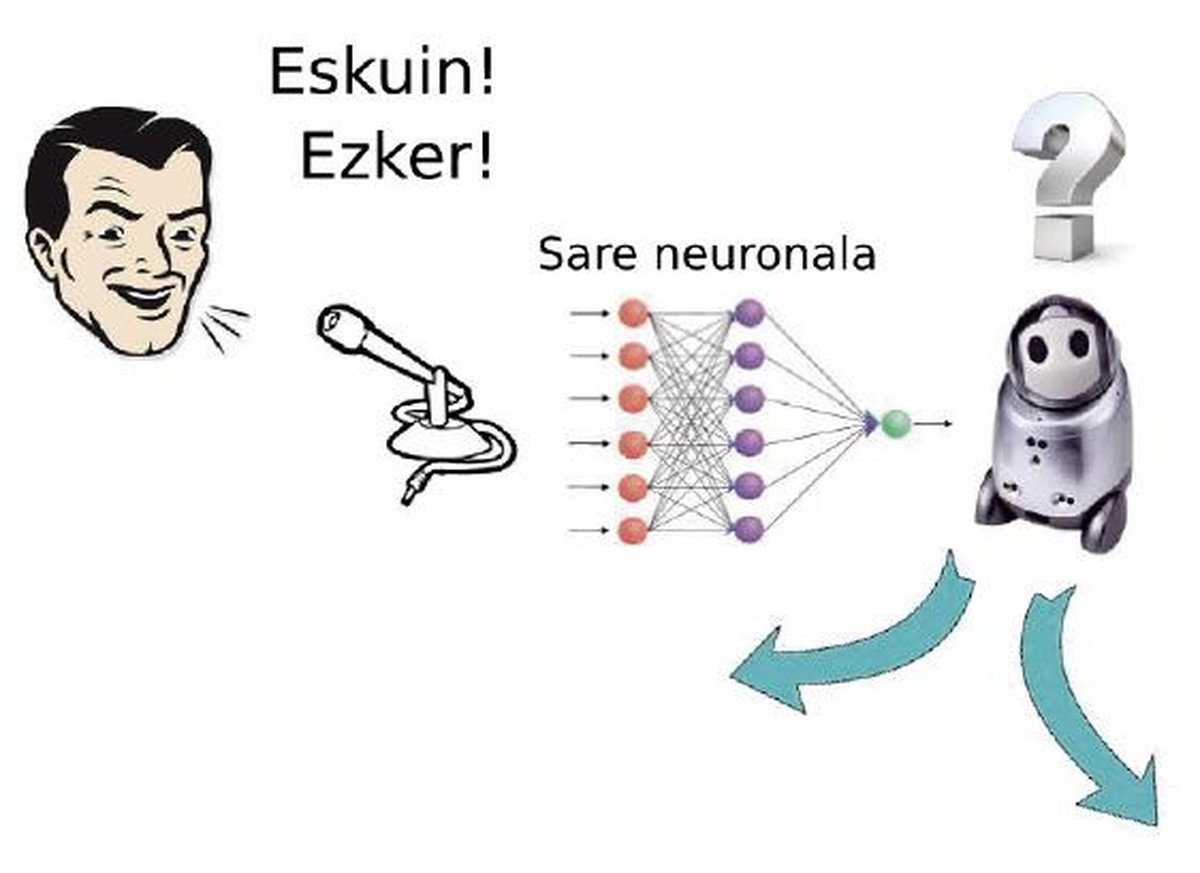
4. irudia. Errefortzu bidezko ikaskuntzaren adibide bat. Robotari agindu bat emango diogu, “eskuin” edo “ezker”, eta, egiten duen mugimenduaren arabera, nota bat jarriko diogu 1etik 10era.

Robotaren helburua da sare neuronala osatzen duten neuronen pisuak lortzea, guk esandakoa ongi egin dezan. Pisu guztien 
balio posible guztien artean badaude-eta soluzio batzuk, ahotsezko estimuluari mugimendu egokiarekin erantzuten dietenak. Horretarako, errefortzu bidezko ikaskuntza erabiliko dugu. Robotari agindu bat emango diogu, “eskuin” edo “ezker”, eta, egiten duen mugimenduaren arabera, nota bat jarriko diogu 1etik 10era. “Eskuin” esan eta ezkerrera mugitzen bada, 1 jarriko diogu. Baina 
aurrera mugitzen bada pixka bat eskuinera eginez, agian 5 bat jarriko diogu. Noski, eskuinera mugitzen denean, 10eko bat izango du!

Ikaskuntza-prozesuak honela funtzionatzen du: lehenik eta behin, algoritmo genetikoak ausazko soluzio batzuk hautatzen ditu, hots, sare neuronalaren pisu zehatz batzuk. Soluzio horiek exekutatzen ditu eta, jasotako sariaren arabera, onenak zein diren ikusten du. Pisu onenak gurutzatzen ditu, mutazioa aplikatzen du batzuetan, eta berriro probak egiten ditu belaunaldi berriarekin. Jasotako sari berriekin, beste belaunaldi bat sortuko da, eta, horrela, ahotsezko agindu guztietarako sari potoloenak jasotzen dituen soluzioa aurkitu arte.

Esperimentu horiek egin dira jada, eta ikusi da teknika horrek funtzionatzen duela. Baina hori ez da magia, matematika baizik. 
Benetan hau ari da gertatzen: funtzio ez-lineal baten parametro egokienak bilatzeko prozesu iteratibo bat. Gure hitzetan, sare neuronalaren pisuak bilatzen ditugu optimizazio-prozesu batean, non lortutako saria maximizatzea baita helburua.

Bukatzeko

Errefortzu bidezko ikaskuntza gizakien eta animalien ikaskuntza-prozesuetan oinarritzen da. Hemen, gainera, erakutsi dugu nola garatu prozesu hori sare neuronalak eta algoritmo genetikoak erabiliz. Batak zein besteak naturan dute oinarria. Liluragarria da ikustea makinei ikasteko gaitasuna eman diezaiekegula. Agian liluragarriagoa da jakitea ikasteko gaitasun hori naturan bertan gertatzen diren prozesuak imitatuz lortu dugula, horrek erakusten baitu zein sakona den urte askoan zientziaren bidez lortu dugun naturaren gaineko ezagutza. Psikologia, biologia, neurozientziak, matematikak eta informatika uztartu ahal izan ditugu makinek ikas dezaten.

Gaur egun, ikasteko gai diren makinen hainbat adibide dauzkagu. Sarean erosten dugunean eta produktuak baloratzen ditugunean, automatikoki aholku berriak jasotzen ditugu, atzean dauden sistemek gugandik ikasten dutelako. Web-bilatzaileek ere ikaskuntza baliatzen dute bilaketa pertsonalizatuak eskaintzeko. Kamara bidez aurpegiak ezagutu, kotxeak modu autonomoan gidatu eta adibide asko jar genitzake ikaskuntzaren eta adimen artifizialaren arrakastaren erakusgarri.

Bidea, hala ere, oraindik luzea da. Hasi besterik ez dugu egin. Adimen artifiziala eta ikaskuntza automatikoa asko garatu diren arren, oraindik urrun gaude gizaki batek egin dezakeenetik. Baina aurrera goaz.

Bibliografia

Russell, S. J., Norvig, P., Canny, J. F., Malik, J. M., Edwards, D. D.: Artificial intelligence: a modern approach. (Vol. 74). Englewood Cliffs: Prentice hall. (1995).
Bishop, C. M.: Neural networks for pattern recognition. Oxford university press. (1995).
Glodberg, D. E.: Genetic algorithms in search, optimization, and machine learning. Addion wesley. (1989).
Melanie, M.: An introduction to genetic algorithms. Cambridge, Massachusetts London, England, Fifth printing, 3. (1999).
Newborn, M.; Newborn, M.: Kasparov vs. Deep Blue: Computer chess comes of age. Springer-Verlag New York, Inc. (1997).
Sutton, R. S.; Barto, A. G.: Reinforcement learning: An introduction (Vol. 1, No. 1). Cambridge: MIT press. (1998).
Lin, L. J.: Reinforcement learning for robots using neural networks (No. CMU-CS-93-103). Carnegie-Mellon Univ Pittsburgh PA School of Computer Science. (1993).
Bellas, F., Duro, R. J., Faiña, A., Souto, D.: Multilevel darwinist brain (mdb): Artificial evolution in a cognitive architecture for real robots. Autonomous Mental Development, IEEE Transactions on, 2(4), 340-354. (2010).
 

"Sarrera honek #KulturaZientifikoa 3. Jaialdian parte hartzen du"

eu es fr en ca gl