Virtual language maps
2018/09/01 Artetxe Zurutuza, Mikel - Hizkuntzaren prozesamenduan doktoregaia EHUn Iturria: Elhuyar aldizkaria
The language is curious. In both writing and pronunciation, the words pig and lice are very similar, while the words pig and wild boar are completely different. Among animals, however, pigs are much closer to boars than lice. In short, the relationship between the words of a language and its meanings is arbitrary, and the relationships between the concepts of pig, louse and wild boar only live in our mind.
However, when you do a Google search or talk to Siri, what we have so internalized becomes a great difficulty for machines. And just like when we lose ourselves on the mountain or on the road, machines use maps to advance the labyrinth of languages. These maps are called Embedding and, through them, the processing of language has been internalized in terrain that seemed unthinkable. We will make that journey step by step.
From city maps to word maps
Before entering the territory of the language, we stop momentarily to look at our common maps. Basically, the maps we know are graphical representations of a territory, for example, that assign a point to each city in each case. Logically, for maps to make sense, these points are not scattered in any way, but the location of the map respects the distances we have in reality. Thus, on a map, Paris will appear closer to Brussels than to Moscow, because in reality the French capital is closer to the Belgian than to the Russian one.
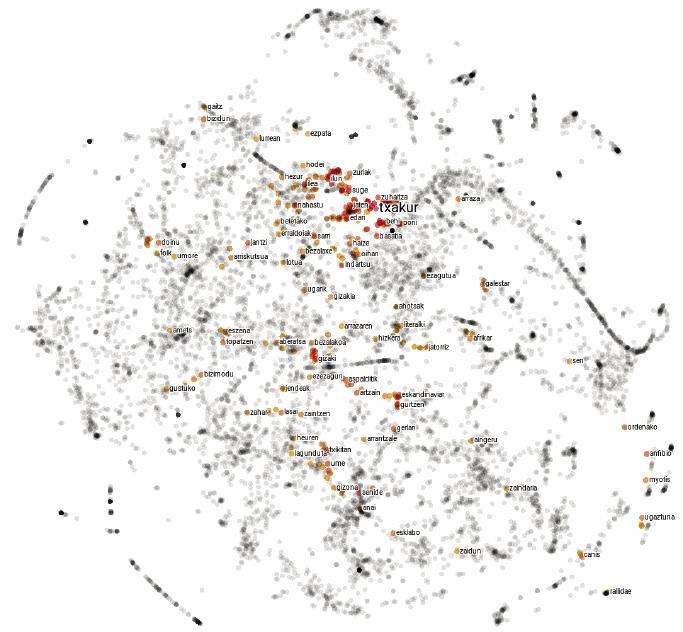
Language maps are not very different. Instead of explaining cities, each point represents a word and the distances between them depend on the semantic similarity of words. Therefore, on a map of this type, the point corresponding to the word pig will be closer to that corresponding to the boar than to the louse, since the semantic similarity between the words pig and boar is greater than between the words pig and lice.
But not everything is so simple: to correctly grasp the complexity of the language, the 2 dimensions of the paper fall short, and these maps usually have about 300 dimensions. But don't be afraid of big numbers! Since there is a leap from a single dimension of the line to the two dimensions of the square, and a leap from the two dimensions of the square to the three dimensions of the cube, you can imagine that there is a similar leap from the three dimensions of the cube to the four of the tenon, and so we could continue until we reach the 300 dimensions cited.
But how to build a 300 dimensional map if we live in three dimensions? Don't worry, we're not going to start! In fact, these maps are not physical but mathematical objects that live in the memory of computers. In fact, all maps can be reproduced by numbers. For this, a reference system is usually agreed, indicating each point according to its position with respect to the different axes. Thus, according to the angular distance from the equator and the meridian of Greenwich, the coordinates of Paris (48.86, 2.35) are those of Brussels (50.85, 4.35) and Moscow (55.75, 37.62). These coordinates allow us, among other things, to calculate mathematically the distances between cities. The same is done with language maps, but as instead of having 2 dimensions, 300 numbers are needed to describe each point. For each of those sequences of numbers representing a word is what we call embedding.
Starting from text and mapping machines
Mapping is hard work. Cartographers collect and analyze various photographs, measurements and statistics, and make graphic representations that match this data. The description of languages has also been made by man: there are, among others, dictionaries that are so common to us. But the maps we are dealing with are not manual. Analyzing long texts, machines create them automatically and is a simple and effective recipe.
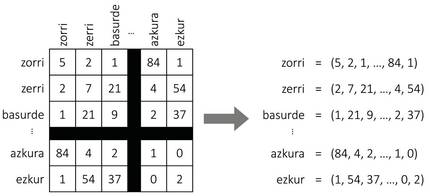
As shown in Figure 2, suppose we build a giant table with all the words of a language. For each word we will have a row and a column, so that each cell fits a couple of words. To fill in the table, we will take a long text and count the number of phrases that appear simultaneously each pair of words. And voilà, we have our map! For each word we will take the list of numbers of the corresponding row, which will be the coordinates of the word.
Even if it seems a lie, this simple approach generates quite sensible maps. In fact, according to the distributive hypothesis of semantics [8, 7], similar words tend to have similar representation patterns, so the previous procedure will assign them similar coordinates. Also for our initial example, the words boar or pig will often appear next to the word acorn and rarely next to the word itch, and with the word zorri will occur the other way around. Therefore, pigs and tiles will have similar coordinates and will be close to each other on the map. The coordinates of lice will be quite different, so you will move away from them.
But there is something missing in this recipe. Although the 300 dimensions mentioned above seemed very much, this procedure would generate maps of tens of thousands of dimensions, since languages will form their coordinates with as many words as numbers. How to reduce the number of dimensions? The answer is not very strange: our common maps usually have two dimensions, although in reality we talk about a three-dimensional world. In fact, when creating maps, the height dimension is usually excluded, since it is not very significant when calculating distances between cities. Something similar is done with the maps of languages: using different mathematical techniques the axes of greater variability (the most significant) are identified and the rest of dimensions are excluded from the map. Despite some adaptations to correct the effect of frequency, this is the basic idea underlying the counting techniques for the study of embeddings [3]; note that machine-learning techniques [11, 4] follow the same procedure implicitly [10].
Playing with maps
Despite its simplicity, our common maps hide more secrets than it seems in principle. Although they have not been designed for this, they also serve to appreciate, for example, the temperature that occurs anywhere in the world. In fact, the points at extreme latitudes, closest to the poles, are usually colder, while the points closest to the equator are hotter. Just as the axis of latitude is related to temperature, in language maps similar axes can also be identified that relate the polarity of words (degree of positivity and negativity) with other characteristics [12]. Thanks to them, automatic review analysis applications have acquired great strength in recent times.
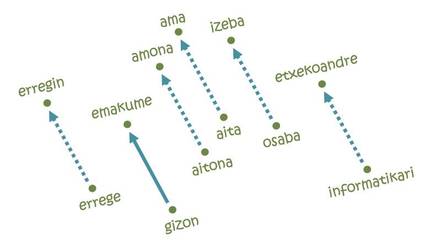
But what has made the embeddings so popular has been the resolution of analogies [11]. The idea cannot be simpler: To go from Paris to Brussels it is necessary to travel 222 km to the North and 144 km to the East; likewise, in each of the axes of the map of the language it will take a certain distance from the word man to the word woman, for example. For if we start with the word king and follow the same steps, we come to the word erregin! In fact, the trajectory studied codifies the man-woman relationship and moves it to its feminine equivalent from any masculine word. Similarly, equivalent analogies can be made for pais-capital, singular-plural, present and past relations.
But not everything is so beautiful: if we start with the word computer science following the same trajectory of men and women, for example, we would talk about housewives [5]. In other words, according to the map, computer science is men's, and housework is women's. What to see, to learn that: the embeddings are based on texts written by human beings and reflect the same discriminatory tendencies rooted in our society. In fact, according to several experts, dealing with such unfair behaviors will be one of the future challenges of artificial intelligence.
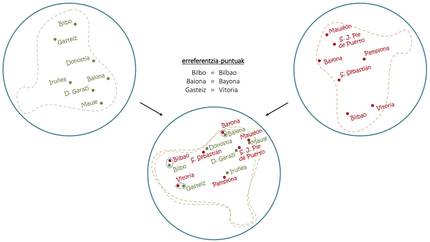
Despite the problems, if with a single language you can do these tricks, combining multi-language maps have achieved even more surprising things. As shown in Figure 4, as with the overlapping of two maps in Basque and Spanish, the Spanish counterperformance of Basque capitals can be extracted, with the embeddings the same basic principle is used to induce translations of common words [1, 6]. In this sense, automatic translators have recently been developed capable of learning without any kind of human conduct [2, 9], of reading long texts in several languages and of making translations among them without other aids.
New destinations
Although our journey is about to reach the end, the path taken by the embeddings seems infinite. Along with improving study techniques and developing new applications, attempts to address longer phrases or texts from word maps have gained strength in recent times. How far that road will take us, but it does not appear on any map and, with new goals on the horizon, the future could not be more exciting.
References
Work presented to the CAF-Elhuyar awards.

Gai honi buruzko eduki gehiago
Elhuyarrek garatutako teknologia





