Mapas virtuales de idiomas

2018/09/01 Artetxe Zurutuza, Mikel - Hizkuntzaren prozesamenduan doktoregaia EHUn Iturria: Elhuyar aldizkaria

• Adimen artifiziala
• Softwarea

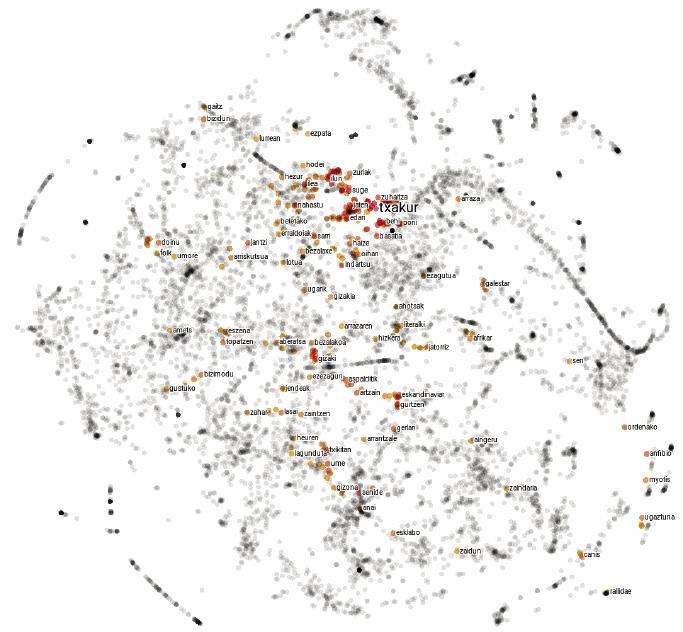
Es curioso el idioma. Tanto en la escritura como en la pronunciación, las palabras cerdo y piojos son muy similares, mientras que las palabras cerdo y jabalí son completamente diferentes. Entre los animales, sin embargo, los cerdos están mucho más cerca de los jabalíes que de los piojos. En definitiva, la relación entre las palabras de una lengua y sus significados es arbitraria, y las relaciones entre los conceptos de cerdo, piojo y jabalí sólo viven en nuestra mente.

Sin embargo, al hacer una búsqueda en Google o hablar con Siri, lo que tenemos tan interiorizado se convierte en una gran dificultad para las máquinas. Y al igual que cuando nos perdemos en el monte o en la carretera, las máquinas utilizan mapas para avanzar en el laberinto de lenguas. Estos mapas se denominan Embedding y, a través de ellos, el procesamiento del lenguaje se ha internalizado en terrenos que parecían impensables. Vamos a hacer ese viaje paso a paso.

De mapas de ciudades a mapas de palabras

Antes de adentrarnos en el territorio de la lengua, paremos momentáneamente para fijarnos en nuestros mapas comunes. Básicamente, los mapas que conocemos son representaciones gráficas de un territorio, por ejemplo, que asignan un punto a cada ciudad en cada caso. Lógicamente, para que los mapas tengan sentido, estos puntos no están dispersos de cualquier manera, sino que la ubicación del mapa respeta las distancias que tenemos en la realidad. Así, en un mapa, París nos aparecerá más cerca de Bruselas que de Moscú, porque en la realidad la capital francesa está más cerca de la belga que de la rusa.

Los mapas de idiomas no son muy diferentes. En lugar de explicar las ciudades, cada punto representa una palabra y las distancias entre ellas dependen de la semejanza semántica de las palabras. Por lo tanto, en un mapa de este tipo, el punto correspondiente a la palabra cerdo estará más cerca del correspondiente al jabalí que al piojo, ya que la similitud semántica entre las palabras cerdo y jabalí es mayor que entre las palabras cerdo y piojos.

Figura . Estudio de Embedding por conteo. A partir de un texto largo, una tabla muestra el número de frases que aparecen simultáneamente cada combinación de palabras. La lista numérica de cada fila da las coordenadas de la palabra correspondiente. En la práctica, esta aproximación básica se suele afinar con técnicas de adaptación de la frecuencia de las palabras y reducción de la dimensionalidad.

Pero no todo es tan sencillo: para captar correctamente la complejidad del lenguaje, las 2 dimensiones del papel se quedan cortas, y estos mapas normalmente tienen unas 300 dimensiones. ¡Pero que no te asusten los grandes números! Como hay un salto de una sola dimensión de la recta a las dos dimensiones del cuadrado, y un salto de las dos dimensiones del cuadrado a las tres del cubo, puedes imaginar que existe un salto parecido desde las tres dimensiones del cubo a las cuatro del tesón, y así podríamos seguir hasta llegar a las 300 dimensiones citadas.

¿Pero cómo construir un mapa de 300 dimensiones si vivimos en tres dimensiones? ¡No te preocupes, no vamos a empezar! En realidad, estos mapas no son físicos sino objetos matemáticos que viven en la memoria de los ordenadores. De hecho, todos los mapas pueden ser reproducidos mediante números. Para ello se suele consensuar un sistema de referencia, indicando cada punto en función de su posición respecto a los diferentes ejes. Así, según la distancia angular con respecto al ecuador y al meridiano de Greenwich, las coordenadas de París (48.86, 2.35) son las de Bruselas (50.85, 4.35) y Moscú (55.75, 37.62). Estas coordenadas nos permiten, entre otras cosas, calcular matemáticamente las distancias entre ciudades. Lo mismo se hace con los mapas de idiomas, pero como en lugar de tener 2 dimensiones, son necesarios 300 números para describir cada punto. Pues cada una de esas secuencias de números que representan una palabra es lo que llamamos embedding.

Partiendo del texto y cartografiando las máquinas

La realización de mapas es un trabajo laborioso. Los cartógrafos recopilan y analizan diversas fotografías, mediciones y estadísticas, y elaboran representaciones gráficas que coinciden con estos datos. La descripción de las lenguas también ha sido realizada por el hombre: ahí están, entre otros, los diccionarios que nos son tan comunes. Pero los mapas que nos ocupa no son manuales. Analizando textos largos, las máquinas las crean automáticamente y es una receta sencilla y eficaz.

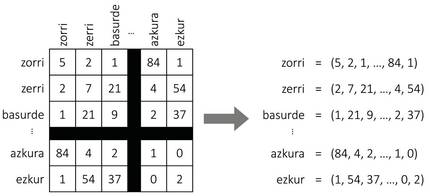
Como se muestra en la Figura 2, supongamos que construimos una tabla gigante con todas las palabras de una lengua. Para cada palabra tendremos una fila y una columna, de forma que cada celda se adapte a un par de palabras. Para rellenar la tabla, tomaremos un texto largo y contaremos el número de frases que aparecen simultáneamente cada pareja de palabras. ¡Y voilà, tenemos nuestro mapa! Para cada palabra cogeremos la lista de números de la fila correspondiente, que serán las coordenadas de la palabra.

Aunque parezca mentira, esta simple aproximación genera mapas bastante sensatos. De hecho, según la hipótesis distributiva de la semántica [8, 7], palabras similares suelen tener patrones de representación similares, por lo que el procedimiento anterior les asignará coordenadas similares. También para nuestro ejemplo inicial, las palabras jabalí o cerdo aparecerán con frecuencia junto a la palabra bellota y pocas veces al lado de la palabra picor, y con la palabra zorri ocurrirá al revés. Por tanto, los cerdos y azulejos tendrán unas coordenadas similares y quedarán próximos entre sí en el mapa. Las coordenadas de los piojos serán bastante diferentes, por lo que se alejará de ellas.

Figura . Resolución de analogías. Parte de una palabra masculina y, a través de una trayectoria humana, alcanza su equivalente femenino.

Pero hay algo que falta en esta receta. Y es que, aunque las 300 dimensiones mencionadas anteriormente parecían mucho, este procedimiento generaría mapas de decenas de miles de dimensiones, ya que los idiomas formarán sus coordenadas con tantas palabras como números. ¿Cómo reducir el número de dimensiones? La respuesta no nos es muy extraña: nuestros mapas comunes suelen tener dos dimensiones, aunque en la realidad se habla de un mundo tridimensional. De hecho, a la hora de crear mapas, suele excluirse la dimensión de la altura, ya que no es muy significativa a la hora de calcular distancias entre ciudades. Algo parecido se hace con los mapas de las lenguas: utilizando diferentes técnicas matemáticas se identifican los ejes de mayor variabilidad (los más significativos) y se excluyen del mapa el resto de dimensiones. A pesar de algunas adaptaciones para corregir el efecto de la frecuencia, ésta es la idea básica que subyace en las técnicas de conteo para el estudio de las embeddings [3]; téngase en cuenta que las técnicas basadas en el aprendizaje automático [11, 4] siguen el mismo procedimiento de forma implícita [10].

Jugando con mapas

A pesar de su sencillez, nuestros mapas comunes ocultan más secretos de lo que en principio parece. Aunque no han sido pensados para ello, también sirven para apreciar, por ejemplo, la temperatura que se produce en cualquier parte del mundo. De hecho, los puntos que se encuentran en latitudes extremas, los más próximos a los polos, suelen ser más fríos, mientras que los puntos más cercanos al ecuador son más calurosos. Así como el eje de la latitud se relaciona con la temperatura, en los mapas de las lenguas también se pueden identificar ejes similares que relacionan la polaridad de las palabras (grado de positividad y negatividad) con otras características [12]. Gracias a ellos, las aplicaciones de análisis automático de opiniones han adquirido gran fuerza en los últimos tiempos.

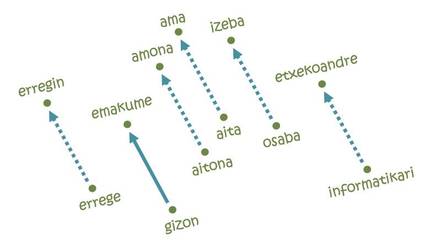
Pero lo que ha hecho las embeddings tan populares ha sido la resolución de analogías [11]. La idea no puede ser más sencilla: Para ir desde París a Bruselas es necesario recorrer 222 km al Norte y 144 km al Este; asimismo, en cada uno de los ejes del mapa de la lengua se necesitará una cierta distancia desde la palabra hombre hasta la palabra mujer, por ejemplo. Pues si empezamos por la palabra rey y seguimos los mismos pasos, ¡llegamos a la palabra erregin! De hecho, la trayectoria estudiada codifica la relación hombre-mujer y la traslada a su equivalente femenino a partir de cualquier palabra masculina. Análogamente, se pueden realizar analogías equivalentes para las relaciones pais-capital, singular-plural, presente y pasado.

Pero no todo es tan bonito: si empezamos por la palabra informática siguiendo la misma trayectoria de hombres y mujeres, por ejemplo, llegaríamos a hablar de amas de casa [5]. En otras palabras, según el mapa, la informática es cosa de hombres, y las tareas domésticas son de mujeres. Qué ver, aprender aquello: las embeddings se basan en textos escritos por seres humanos y reflejan las mismas tendencias discriminatorias arraigadas en nuestra sociedad. De hecho, según varios expertos, afrontar este tipo de comportamientos injustos será uno de los retos futuros de la inteligencia artificial.

Figura . Mapeo de Embedding. Dos mapas de Euskal Herria, uno en euskera y otro en castellano, orientados de diferente manera, se superponen entre sí acercando a los pares urbanos de referencia (Bilbao-Bilbao, Baiona-Bayona, Vitoria-Gasteiz). Una vez hecho esto, se pueden extraer nuevas parejas de traducción atendiendo a los puntos que han quedado juntos en el mapa superpuesto (por ejemplo, se puede concluir que la contraprestación de Pamplona es de Pamplona al ver que los puntos correspondientes han quedado juntos). Con los mapas lingüísticos también se utiliza este principio básico para inducir traducciones de palabras comunes.

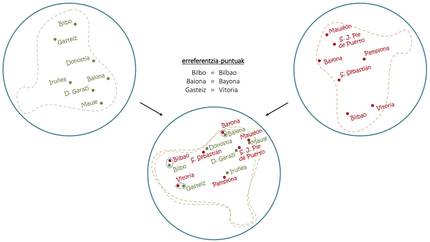
A pesar de los problemas, si con una sola lengua se pueden hacer estos trucos, combinando mapas de varios idiomas se han conseguido cosas aún más sorprendentes. Tal y como se observa en la figura 4, al igual que con la superposición de sendos mapas en euskera y en castellano se pueden extraer las contraprestaciones en castellano de las capitales vascas, con las embeddings se utiliza el mismo principio básico para inducir traducciones de palabras comunes [1, 6]. En este sentido, recientemente se han desarrollado traductores automáticos capaces de aprender sin ningún tipo de conducción humana [2, 9], de leer textos largos en varios idiomas y de realizar traducciones entre ellos sin otras ayudas.

Nuevos destinos

Aunque nuestro viaje está a punto de llegar al final, el camino recorrido por las embeddings parece infinito. Junto a la mejora de las técnicas de estudio y el desarrollo de nuevas aplicaciones, los intentos de abordar frases o textos más largos a partir de mapas de palabras han cobrado fuerza en los últimos tiempos. Hasta dónde nos llevará ese camino, pero no aparece en ningún mapa y, con nuevas metas en el horizonte, el futuro no podía ser más emocionante.

Referencias

Trabajo presentado a los premios CAF-Elhuyar.