Infinito
1998/10/01 Angulo, Patxi Iturria: Elhuyar aldizkaria
O infinito é difícil de definir e todas as definicións terán argumentos a favor e en contra. Si dirixímonos a un vocabulario común defínese como aquel que non ten fin e non pode ser indefinido. A definición é detallada e parece razoable. A intuición tamén vai por aí, pero agora preguntámonos hai algo que non ten límites? Si non houbese nada sen límites, non definiriamos nada. Por tanto, hai que buscar algo sen límites.
A primeira idea que vén á mente é o universo, porque é o máis grande que coñecemos. Con todo, fai 2.000 anos Arquímedes demostrou que o universo era tamén finito cando calculou o número de grans de area necesarios paira encher o universo, menos de 1063. A pesar da súa gran cantidade, é finita. Moitas veces os seres humanos mesturamos infinito e cousas grandes. Moitas cousas son grandes pero teñen límites. Por tanto, non son infinitos.
Isto esgota todas as posibilidades existentes no mundo real/físico. Por tanto, temos que ir ao mundo da imaxinación. No mundo da imaxinación atopamos os maiores obstáculos paira comprender o infinito, xa que o mundo da imaxinación é amplo e sen límites. Doutra banda, cada un ten a súa propia imaxinación e paira entendernos con outro amigo, o mundo das ilusións que eu tiña ten que unir.
O propio Arquímedes deunos a idea de atopar algo sen límites. El calculou a cantidade de grans de area necesarios paira encher o universo. Este número de grans, 1063, era un número natural finito. Pero os números que utilizamos paira contar son finitos? Non, claro. Aí está algo ilimitado, o conxunto dos números naturais,
N = {1, 2, 3, 4, 5, ..., 1.000.000, 1.000.001, ..., 1063, ...}.
Si engadimos aos números naturais os opostos, os negativos e os 0 obteremos números enteiros, que tamén son infinitos:
Z ={...., -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, ...}.
O conxunto de números enteiros é a parte do conxunto de números racionais. Por tanto, os números racionais tamén son infinitos:
Q = anteriores..., -3, -1/3, -1/2, -2, -1, 0, 1, 2, 1/2, 1/3, 3, ...}.
Finalmente, engadindo irracionais aos números racionais (…e,p,…) obteremos números reais que tamén son infinitos. Por tanto, elaboramos una cadea como a seguinte:
N C Z C Q C R.
Nel todos os conxuntos son infinitos.Cando
contamos os elementos dos conxuntos finitos defínese a aplicación bijetiva entre o conxunto e un subconjunto do grupo N. Por exemplo, conxunto de vogais = {a, e, i, ou, ou}. Cantos elementos ten?
a -1, e -2, i -3, ou -4, ou -5
Por tanto, entre os grupos {a, e, i, ou, ou} e {1, 2, 3, 4, 5} definimos una aplicación bijetiva.Os grupos finitos
teñen distintos elementos: o conxunto de vogais 5 elementos, o conxunto de consonantes 21 elementos. Que pasará cos conxuntos infinitos?
Paira saber cantos elementos hai no grupo Z máis que no grupo N utilizaremos o hotel infinito, o hotel N. Supoñamos un hotel con infinito habitacións (1º, 2º, 3º, …) todas as habitacións están cheas. Debido a unha mala comunicación, un grupo de infinitos amigos adiántase un día e os responsables do hotel deben proporcionarlles una habitación paira corrixila. Como introducirán os novos infinitos amigos (-1, -2, -3, ...) en cada habitación os responsables do hotel?
Una solución pode ser: (-1) meter ao novo amigo na habitación 1, meter ao compañeiro da habitación 1 (1) na habitación 2, meter ao compañeiro da habitación 2 (2) na habitación 3 e así cos demais. Ao primeiro amigo adaptámoslle a súa habitación. Agora situaremos (-2) ao segundo amigo. Introducimos ao compañeiro (-2) na habitación 1, pasamos ao compañeiro (-1) na habitación 1 á habitación 2. Amigo de 2º (1) habitación a 3º e así cos demais. En xeral, paira introducir un novo amigo, empezando pola primeira habitación, as persoas que se atopen nas habitacións pasarán ás seguintes habitacións e deixaremos o primeiro baleiro.
No último momento (0) chegaron novos amigos a buscar sitio. Seguindo o procedemento anterior, baleiraremos a 1ª habitación paira acceder a ela.
Así pois, no Hotel N había amigos 1, 2, 3, ... e incluímos -1, -2, -3, ... e 0 persoas, adaptando cada un deles nunha habitación. En consecuencia, podemos dicir que hai tantas persoas como habitacións. É dicir, teñen tantos elementos como os grupos Z e N.
| Habitacións |
1. | 2. | 3. | 4º | 5. | ... |
Hotel completo |
1. | Servizos | Servizos | Seguridade | Servizos | ... |
Introducir un novo amigo |
-1 | 1. | Servizos | Servizos | Seguridade | ... |
Engadir novo amigo 2 |
-2 | -1 | 1. | Servizos | Servizos | ... |
Outro día volvemos a atopar o hotel N cheo. Pero ao mediodía infinitas persoas deixaron o hotel. Estimados amigos, 4º, 6º, … estaban nas habitacións. Por tanto, a metade das habitacións quedaron baleiras. Pola tarde veu outro grupo infinito (1,2,3, ...). Os responsables do hotel non tiveron problemas paira adaptarse ás habitacións baleiras. (1) meter ao compañeiro na habitación 2, (2) ao compañeiro na habitación 4, (3) ao amigo na habitación 6 e así cos demais.
| Habitacións |
1. | 2. | 3. | 4º | 5. | 6º | ... |
Hotel completo |
a) | b) | c) | d) | e | f) | ... |
Medio hotel baleiro |
a) | c) | e | ... | |||
Hotel de novo cheo |
a) | 1. | c) | Servizos | e | Servizos | ... |
Podemos dicir que no centro das habitacións metemos tantas persoas como en todo o hotel. Noutras palabras, un conxunto infinito (1,2,3,...) pode ter tantos elementos como subconjuntos infinitos (2,4,6,...).
O seguinte grupo é Q, os números racionais son cocientes entre dous números enteiros, sen que o divisor sexa 0. Os cocientes paira contar os números do grupo Q serán considerados como un número único. Como no caso anterior, demostraremos que no grupo Q hai tantos números como no grupo N mediante unha aplicación bijetiva. Esta aplicación proporcionarémola mediante unha táboa na que só aparecerán os números positivos, pero os números negativos contabilizaranse da mesma maneira.
Os números que indican as fraccións entre parénteses xa apareceron. Por iso non se computan na táboa inferior.
1349101827…281626…5715192939…6142538…11132024374353…123652…21233035445168…22345067…..........................A partir desta táboa pódese comprobar que por cada elemento do grupo N hai un elemento do grupo Q e pola contra, por cada elemento do grupo Q hai un elemento do grupo N. En definitiva, pódese demostrar que a aplicación é un bijetivo.
Todos estes infinitos conxuntos parecen ter o mesmo número de elementos, A1. No grupo seguinte, R, ademais dos números racionais, inclúense os números irracionais. Cantos son os números irracionais? Antes de contar todos os números reais contabilizaremos os comprendidos entre 0 e 1.
Comprobamos que no intervalo (0,1) hai máis números que no grupo N. A idea da demostración é: Supomos que entre os grupos N e (0,1) a aplicación bijetiva está definida e veremos que un número situado entre 0 e 1 non ten imaxe no grupo N. Por tanto, concluiremos que non é posible definir este tipo de aplicacións. de onde se deduce que no grupo (0,1) hai máis elementos que no grupo N. Este maior número de elementos denominarase c e cumprirase con A1 < c. Imos explicar a demostración.
Si entre os grupos N e (0,1) estivese definida a aplicación bijetiva, poderiamos escribir a seguinte correspondencia:
Números naturais (0,1)alternos intercalos10,a1a2a3a4a5 ...20,b1b2b3b3b4b5 ...30,c1c2c3c4c5 ....40,d1d3d4d5 ....50,e1e2e3e4e5 ..........
Á esquerda todos os números naturais e á dereita, en forma decimal, todos os elementos do grupo (0,1). Tomemos os seguintes números:
z1a1, z2b2, z3c3, z4d4, z5e5,...
e completemos o seguinte número decimal:
0,z1z2z3z4z5...
Este número está entre 0 e 1 e non é o mesmo que os que aparecen á dereita porque así eliximos (z1a1, z2b2, z3c3, z4d4, z5e5, ...). Por tanto, non corresponde ningún elemento do grupo N situado á esquerda. No grupo (0,1) hai máis elementos que no grupo N.
O rango (0,1) é só una pequena parte do conxunto R, pero ten máis elementos que o conxunto N. Comparemos agora os grupos (0,1) e R. A comparación realizarémola mediante unha figura xeométrica.
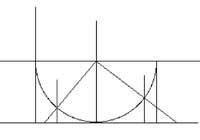
No eixo OX das coordenadas do plano sitúase o intervalo (0,1). (1/2,1/2) debúxase una semicircunferencia superior con centro e radio 1/2. Desde o punto x do intervalo (0,1) elévase una vertical até alcanzar a media circunferencia. Debúxase a recta que pasa polo centro da circunferencia e polo punto anterior. Esta recta cortará o eixo OX no punto e. e é o punto correspondente a x. Tamén se pode facer ao revés. Tomando o punto e´ do grupo R, debúxase a recta que une este punto co centro da circunferencia. Esta recta curta a semicircunferencia nun punto. Desde este punto baixa unida ao eixo OX até atopar o eixo OX no punto x´. x´ corresponde ao momento e´.
Así, entre os grupos (0,1) e R definiuse una aplicación bijetiva. Isto significa que os grupos (0,1) e R teñen o mesmo número de elementos, é dicir, c.
Igual que o número 1 é o seguinte 2 do número natural, podemos chamar A2 ao seguinte do infinito A1 e A3 ao seguinte e así sucesivamente. Tamén atopamos o infinito c e demostramos que A1 < c. A pregunta que nos vén agora á mente é: existe o infinito c A2? É dicir, existe c = A2? Esta pregunta está polo momento pendente de resposta.
A aritmética dos números finitos é coñecida, mentres que a dos números infinitos non. Poderíase demostrar que:
A1 + n = A1c + n = cA1 + A1 = A1c + A1 = cn . A1 = A1c + c = cA1 . A1 = A1n . c = c(A1)n = A1c . c = c(2)A1 = (A1)A1 = c(c)n = c(c)A1 = c(2)c = (c)c = (c)c = outro infinitoA1 N é o número de elementos dos conxuntos Z e Q. c é o
número de elementos do conxunto R. En todos eles n
é o número normal.
O resultado final significa que hai diferentes números infinitos.




