Kode sekretuak (I, II, III)
1993/11/01 Angulo, Patxi Iturria: Elhuyar aldizkaria
Gaiari heldu baino lehen, kriptologiako zenbait hitz teknikoren zerrenda emango dugu, irakurleak aldez aurretik ezagutu dezan.
Zifrario, kode sekretu edota idazkera sekretu adierazpenek esanahi bera dute, transkripzio-arauen sistema, informazio sekretuak dituen jatorrizko mezua irakurri behar ez duten lagunentzat zifratu edo kriptograma izeneko mezu ulertezin bihur dadin.
Igorleak hartzaileari kriptograma bidaltzen dio eta horrek deszifra dezake, gakoa duelako.
Gakoa jatorrizko testua testu zifratu (eta alderantziz) bihurtzeko erabiltzen den arau sekretua da.
Kriptografia zifrarioak egiten irakasten duen arloa da. Kriptoanalisia alderantzizkoa da, hots, zifrarioak bortxatzen irakasten duen arloa. Beraz, kriptografia eraikikorra da; kriptoanalisia, ordea, suntzitzailea. Bi arlo horiek ezin dira banandurik aztertu eta biok Kriptologia izeneko zientzia osatzen dute.
Terminologia zorroztuz, hauxe esango dugu: deszifratu mezuaren hartzaileak egiten du, eta espioiak kriptograma deskriptatu egiten du.
Historian zehar kriptografiak metodo desberdinak erakutsi dizkigu. Gizartea garatu ahala kriptografiaren inportantzia nabarmendu egin da. Ondorioz, gero eta zifrario konplexuagoak agertu izan dira. Baina gutxi izan dira baliozkoak, baliozkotzat deszifratzen errazak baina deskriptatzeko ezinezkoak direnak hartzen baditugu.
Oinarrizko zifrarioak ordezkapen-zifrarioak eta tokialdaketako zifrarioak ditugu. Lehenengoetan jatorrizko mezuaren letra bakoitzak ordezkari finko bat du mezu zifratuan. Bigarrenetan mezu zifratuaren letrak jatorrizkoaren berberak dira, baina beste ordena batean kokaturik.
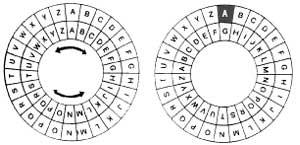
Ordezkapen-zifrarioen artean biraketa-zifrarioak ditugu. Mezua zifratzeko bi disko zentrukide erabiltzen dira, bi diskoak bira daitezkeelarik. Bietan alfabetoko letrak agertzen dira (finkatzeko 26 letra: A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, P, Q, R, S, T, U, V, W, X, Y, Z). Gakoa letra bat da, esaterako G letra. Kanpoko diskoko A letrari barruko diskoko G letra egokituz, alfabetoko gainerako letrei dagozkien letrak azalduko dira (1. irudia). Zifratzeko diskoak kanpotik barrura begiratu behar dira eta deszifratzeko alderantziz begiratuko dira. [Bi diskoen artean aplikazio bijektiboa ezarri dugula esan dezakegu].
Hala ere, zifrario horrek 26 gako besterik ez ditu. Hortaz, espioiak ezer susmatuko balu, 25 proba egitea nahikoa izango luke mezua deskriptatzeko. Hori da, hain zuzen ere, kriptoanalisiaren oinarrizko teknika: bilaketa exhaustiboa.
Gako gehiago izateko asmoz bigarren alfabetoa zoriz ordena liteke, horrela 26! permutazio desberdin izango genuke (hogeita hamar bat zifrako zenbakia). Baina, kopuru horrek mezua babesten al du?
Erantzuna Edgar Allan Poe-k 1843an eman zigun “Urrezko kakalardoa” liburuan (irakurtzea gomendatzen dizugu). Poek kontatzen digun istorioan, Legrand izeneko lagunak Kidd itsaslapurraren zifrarioa deskriptatzea lortu zuen. Horretarako metodo estatistikoa erabili zuen, hau da, jatorrizko hizkuntzako letren maiztasuna zifrarioaren ikurretan isladatzen da. Deskriptaketa burutzeko letrak banaka, binaka eta hirunaka hartzen dira. Horrela letrei dagozkien ikurrak aurki daitezke (1. taula).
(Taulan, inguruko hizkuntzetako letrak eta letren bikote eta hirukoteak maiztasunaren arabera ordenaturik agertzen dira. Horrez gain, gehien erabiltzen diren letren eta bokalen portzentaiak ere ikus ditzakegu.)
Metodo estatistiko horiek XV. mendearen hasieran jadanik deskribatu zituen Qalqashandi-k, bere aitzindari izan zen Ibn ad-Duraihim-i (1312-1361) leporatu zizkiolarik. Mendebaldean, analisi kriptografikoari buruzko lehenengo tratatua 1474ean eman zuen argitara Cicco Simonetta-k, Milango sforzatarren kantzelaritzako idazkariak.
Estatistika engainatzeko bi zifrario-mota erabili dira: homofonoak eta izendegiak. Zifrario homofonoa, alfabetokoak baino letra (edota ikur) gehiago erabiltzean datza. Erabilitako hizkuntzaren letrarik ohizkoenak bi letraren (edota ikurren) bidez zifratzen dira, mezu zifratuen letren maiztasunak aldatuz (2. irudia). Beste aukera bat, ulergarritasuna galdu gabe jatorrizko testuan letra nuluak tartekatzea izan daiteke. Letra nulutzat maiztasun gutxiko letrak erabili ohi dira. Bi metodoek maiztasunak orekatzeko joera dute; lehenengoak maiztasun handienak txikiagotuz eta bigarrenak maiztasun txikienak handiagotuz. Sistema hauek duten arriskua mezua gehiegi luzatzearena da.

XVI. mendetik XIX. mendearen lehenengo erdira arte posta-truke diplomatikoan gehien erabilitako sistema, izendegi izeneko sistema nahasia izan da. 3. irudian Sir Francis Walsingham-ek, Ingalaterrako erreginaren Frantziako enbaxadoreak, erabiltzen zuen izendegia agertzen da. Funtsean zifrario homofonoa da. Hala ere, izendegiek beste ezaugarri bat dute: maiz erabili behar den hitz edo gaiei ikur bereziak egokitzen dizkiete.

Letren maiztasuna manten dadin dagoen beste aukera bat, zifrario polialfabetikoak erabiltzean eta zifraketan zehar gakoak aldatzean datza. Horrela jatorrizko letra bera, mezuan duen lekuaren arabera, mezu zifratuaren letra desberdin bihurtuko da.
Blaise de Vigenère-ren (1523-1596) zifrarioan gakoa hitz bat zen; jatorrizko testuaren azpian errepikaturik idazten zena. Taula batean 26 lerrotan alfabetoko letrak 26 aldiz idazten ziren, ezkerrera leku bat mugituta. Mezua zifratzeko jatorrizko mezuaren letra eta bere azpian zegoen gakoaren letra, hurrenez hurren, zutabetan eta errenkadetan bilatu eta bion arteko gurutzean zegoen letra izango zen ordezkoa (4. irudia).

Denbora luzez Vigenère-ren zifrarioa deskriptaezina zela uste izan zen. Zifratu polialfabetikoen aurkako lehenengo metodoa eman zuena Friedrich Kasiski (1805-1881) prusiarra izan zen. Kasiski zifrario batzuetan letra-multzo bat zenbait leku aurrerago errepikatzen zela ohartu zen. Hortik, gakoaren letra-kopurua errepikaturiko letren arteko distantziaren zatitzailea zela ondorioztatu zuen. Esate baterako, errepikatzen diren letra-multzoen artean 18 leku badago, gakoaren letra-kopurua 1 (zifrario monoalfabetikoa), 2,3,6,9,18, izango da (5. irudia).
Metodo horrek ez zuen beti balio; letra-multzoak errepikatzen ez zirenean esaterako. Baina horretarako gako luzeak behar dira. Nola libratu, beraz, Kasiski-ren metodotik gakoa luzeegia izan gabe?
Johannes Trithemius-ek gakotzat alfabeto osoa erabiltzea proposatu zuen, Gronsfeld-ek lehenengo 10 errenkada besterik ez erabiltzea eta bakoitzari zenbaki bana egokituz gakoa zenbakien bidez ematea. Beaufort-ek, ordea, bi aukera eman zituen: a) lehenengo errenkadan jatorrizko letra bilatu, zutabetik jaitsi gakoaren letra aurkitu arte eta bere errankadaren lehenengo letra da zifratua; b) lehenengo errenkadan gakoaren letra bilatu, zutabetik jaitsiz jatorrizko letra bilatu eta errenkada berean dagoen lehenengo letra da zifratua.
Vigenère-k berak eta Belaso-k beste bat proposatu zuten: zifrario autogakoduna, alegia. Gakoak mezuak adina-letra zuen, hasieran hitz gakoa idazten zen eta ondoren mezua bera (6. irudia). Horrela letra-multzoak errepikatzeari ekiditen zioten. Irakurleari uzten diogu gakoa ezagutuz nola deszifratzen den asmatzea.


Kode sekretuak (II)
Orain arte ordezkapen-zifrarioak ikusi ditugu eta aurrerantzean lekualdaketako zifrarioak aztertuko ditugu. Gehienak saretxoen erabilpenean oinarritzen dira. Badirudi Girolamo Cardano zientzilariak sartu zituela kriptografian.
Julio Verne (1828-1905) idazleak hiru elaberritan erabili zuen kriptografia, Lurraren zentrurainoko bidaia, Mathias Sandorf eta “La jangada” lanetan, hain zuzen. Mathias Sandorf elaberrian Julio Vernek saretxoen erabilpena xeheki azaldu zuen.
Saretxoen sistema erabiltzeko kartulina batean 6x6 laukiz osatutako karratua irudikatzen da (6 hautazko kopurua da) (7. irudia). Horietako batzuk zulatu egiten dira, buelta laurdeneko lau biretan espazio guztiak (hots, karratu handi osoa), bat ere errepikatu gabe, bete daitezen. Mezuaren letrekin 6 letrako 6 talde osatuko dira, behar adina aldiz (azkeneko taldea osatzeko letra gehiago behar bada sartu egingo da).
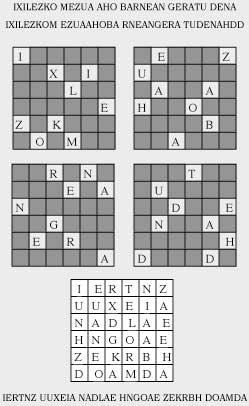
Beste tokialdaketa-sistema bat zutabekakoa da. 6 zenbakia berriro ere aukeratuz, mezua 6 letrako taldetan, bata bestearen azpian kokatuz, banatzen da. Mezua zifratzeko permutazio bat erabiliko da, adibidez (263541), hau da, jatorrizko 2. zutabea lehenengoan idatzi behar da, 6. zutabea bigarrenean, 3.a hirugarrenean, 5.a laugarrenean, 4.a bostgarrenean eta 1.a seigarrenean. Mezuak banatutakoan karratu-itxura duenean, gako bera errenkadak lekuz aldatzeko ere erabil daiteke. Zenbakizko gakoa hitz batez ordezka liteke, ESKOLA = (263541), zenbakiek agertzen diren letren ordena adierazten dute.
Saretxoen sistemak duen arriskua, espioiak lortutakoan mezua errazegi deskriptatu ahal izatea da. Hortik kriptografia modernoaren printzipio nagusietako bat sortu zen.
Kriptografia bi arlotan bereiztu behar da: batetik kriptografia estrategikoa eta bestetik taktikoa. Lehenengoak mezuen sekretua urtetan bermatu behar du. Bigarrenak, aldiz, ordu-pare batean edo egun batean. Guzti hori oso erlatiboa denez, laburbilduz denbora luzean edo laburrean bermatu behar duela esan dezakegu.
Mezu bat zifratzeko bi erabaki hartu behar dira: zifrarioa eta gakoa. Auguste Kerckhoffs von Nieuwenhof (1835-1903) kriptologoak kriptografia estrategikorako gakoaren garrantzia azpimarratu zuen.
Sistema estrategiko baten segurtasuna, gakoaren sekretuan oinarritzen da erabat. Etsaiak zifrario-mota aurkitu badu baina deszifratzeko gakoa ezagutzen ez badu, mezuaren sekretua bermaturik dago.
Kerckhoffs-ek enuntziatutako printzipioak ondoko seietara laburbil daitezke:
- Zifratzeko sistemak, teorian ez bada, praktikan sartuezina behar du izan.
- Sistema arriskuan egoteak, ez ditu igorlea eta hartzailea salatu behar.
- Gakoak, gogoratzeko eta aldatzeko erraza behar du izan.
- Kriptogramek telegrafoz (gaur egun ordenadorez) transmititzeko egokiak behar dute izan.
- Zifratzeko tresnak eta agiriak, garraiatzeko modukoak behar dute izan, pertsona bakar batek eraman ditzan.
- Sistemak xinplea behar du izan, arau-zerrenda luzerik eta ahalegin handiren beharrik gabe.
Gako bakarra (finkoa) duten zifrario batzuk ikusi ditugu, horiei zifrario endakatu, edo kode-zifrario edo laburbilduz kode deitzen zaie. Kode ezagunetakoak Morse-ren kodea eta ordenadoreetan erabiltzen den ASCII kodea ditugu. Esaterako, telefonoetan jatorrizko hitzak kode batez zifratzen dira, eta mezua, entzulearentzat ulergarri bilakatzeko deszifratu egiten da.
Orain arte ikusi ditugun zifrario guztietan letrak banan-banan ordezkatzen ziren. Horregatik deritze monografiko. Orain zenbait zifrario poligrafiko ikusiko dugu.
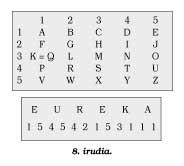
Polibio-ren dameroan 25 letra erabiltzen dira (K = Q eginez), karratu oso bat osatzeko. Letra bakoitza errenkada eta zutabe banatan dago (8. irudia). Zifrarioak letra bakoitzari dagoeneko errenkada eta zutabearen zenbakiak egokitzen dizkio. Letrak karratuan kokatzeko era desberdinak ditugu: alfabetoaren arabera (errazegia), zoriz aukeratuak (karratua beharrezkoa litzateke deszifratzeko), hitz-gako bat hasieran eta ondoren alfabetoaren arabera. Polibioren zifrarioa monografikoa da, baina hurrengoak deskribatzeko abiapuntua.
Playfair-en zifrarioa bigarren mundu-gerran erabili zen. Dameroan hitz-gakoa eta gainerako letrak idazten dira. Mezua letra-bikoteka zatitzen da, hurrengo kasuak agertuko direlarik:
- bi letrak errenkada berean daude. Eskuinean dituzten letrez ordezkatzen dira (azkena lehenengoaz ordezkatuz);
- bi letrak zutabe berean daude. Azpian duten letraz ordezkatzen dira (azkena lehenengoaz ordezkatuz);
- bi letrak errenkada eta zutabe desberdinetan daude. Bi letrak beste birekin laukizuzen baten erpinetan daude, letra bakoitza errenkada berean dagoen erpineko letraz ordezkatzen da;
- bi letrak berdinak dira. Nuluak tartekatzen dira edo biak bakar bat bailiran hartuko dira (9. irudia).

Zifrario hori ez zuen Lyon Playfairek berak asmatu; Charles Wheatstone (1802-1875) zientzilariak baizik.
Felix-Marie Delastelle (1840-1902), Bazeries, Kerckhoffs eta Viaris bezala, Frantziako eskolakoa zen, baina besteak ez bezala hau zale hutsa zen. Bere zifrario erdibituaren abiapuntua 5x5 karratua dugu. Zifraketa hiru etapatan burutzen da: lehenengoan mezua bost letrako taldetan banatzen da (horrek ez du eraginik), letra bakoitzaren azpian dagokion zutabearen zenbakia idatziko dugu eta horren azpian errenkadarena; bigarren etapan bloke bakoitzeko zifrak horizontalean idatziko ditugu, binaka taldekatuta (10. irudia); hirugarren etapan karratua alderantziz erabiliko dugu, zifra-bikoteek letra bana emango digute (zutabe-errenkada).
Delastelleren zifrarioak jatorrizko mezua ongi nahasten du. Hala ere ordenadoreen garaian ezin da segurua denik esan.
Izendegien ondorengoak, hiztegi-zifrarioak edo zerrendazko zifrarioak dira. Hauetan hitzen zerrenda bat (hiztegia) osatzen da eta hitz bakoitzari kode sekretuaren zenbaki bat (edo hitz bat) dagokio. Horiek duten arazoa, hiztegiak handiegiak izatea da. Beraz gordetzen zailak dira. Hiztegiak labur daitezke ohizko esaldiei zenbaki bat egokituz, edo familia bereko hitzak zenbaki bakar batez ordezkatuz.
Beste aldetik, hiztegiko hitzak eta dagozkien zenbakiak ordena arruntean sailkatzen badira, hitz baten ordezkoa aurkituz gero besteenak erraz bila litezke. Hortaz, zoriz sailkatzea litzateke egokiena. Baina horrek hitza-zenbakia eta zenbakia-hitza hiztegien beharra sortzen du. Hiztegi bikoitz horiek serioagoak izan arren, bortxatu izan dira; gako finkoa baitute. Hiztegi-zifrarioek ez dute Kerckhoffs-en printzipioa betetzen; zifrario taktikoak izanik gakoa aldatzea oso zaila baita.

Kode sekretuak (eta III)
Orain arte eskuzko kriptografiaz aritu gara. Hemendik aurrera ordea, kriptografia mekanikoaz mintzatuko gatzaizkizu.
XVIII. mendearen bigarren erdian industri iraultza hasi zen. Orduan makinekiko grina jarrera filosofiko bihurtu zen. Makinak arlo guztietan eraiki eta erabiltzen ziren eta kriptografia ez zen salbuespena izan.
Thomas Jefferson-ek (1743-1826) eta Etienne Bazeries-ek (1846-1931) zifratzeko makina antzekoak asmatu zituzten. Jeffersonen makina zilindro bat eta 26 diskoz osatua zegoen. Diskoen ertzetan 26 letra, ordena desberdinetan, agertzen ziren. Mezua 26 letrako bloketan banatzen zen. Gakoa 1etik 25erainoko zenbaki bat zen (11. irudia). Mezua errenkada batean idatzi eta gero, gakoa 15 bazen, zifratua 15. errenkadan agertuko zen. Makina hark akats bat bazuen: 25 gako besterik ez izatea.

Aurrekoan bezala Enigma izeneko zifratzeko makinan oinarrizko elementua errotorea zen, baina makina hori elektromekanikoa zen. Errotoreek 26na kontaktu elektriko zituzten alde bakoitzean. Bi aldeetako kontaktuak desberdin konektaturik zeuden, kontaktu bati bakar bat zegokiolarik. Ezkerreko lehenengo errotorea finkoa zen. Besteak ordea, norantza berean bira zitezkeen (12. irudia). Errotore bakoitzaren irteerako kontaktuak hurrengoaren (eskuinekoaren) sarrerako kontaktuekin bat zetozen. Lehenengo errotoreak bira oso bat ematen zuenean, bigarrenak bira baten 26rena ematen zuen; bigarrenak bira osoa emandakoan hirugarrenak bira baten 26rena ematen zuen. Hala segitzen zuen errotore guztiekin. Guztira 26n aukera zituen, n errotore-kopurua izanik.
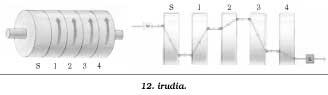
Beraz, ordezkapen polialfabetikozko zifrarioa zen. Gako-aukera handia izateak zifrarioa bortxaezina zela pentsaraz diezaguke. Hala ere, Bigarren Mundu Gerran kriptoanalista aliatuek Enigma deskriptatu egin zuten, alemaniarren akats batzuei esker eta kalkulu-makina erraldoien laguntzaz. Kontraespioitzan ibilitako bat Alang Turing (1912-1954), informatika teorikoaren sortzailea, izan zen. Enigma makinak oztopo bat zeukan; inprimagailurik ez izatea, hain zuzen.
Zifrarioen segurtasun-maila hobetzeko, homofonoak, nuluak eta poligrafiaz gain zifrario gehiago ere erabil daiteke, hots, zifrario konposatuak. Zifrario konposatuetan segurtasun-maila zifrarioen segurtasun-mailen batura dela pentsa genezake, baina ez da horrela. Irakurleak berak egiazta lezake bi biraketa-zifrario konposatuz. Bestalde, zifrarioen segurtasun-mailarekin batera konplexutasuna ere handiagotzen da. Beraz, logikoa dirudi segurtasun-mailen batura ez eta maila handiagoa, biderkadura adibidez, lortzen saiatzeak.
Hori da ia-ia Vigenère-ren bi zifrario konposatuz lor daitekeena. Gakoek lehenengo zifrarioan N letra eta bigarrenean M letra dutenean, zifrario konposatuaren gakoak aurreko bi zenbakien multiplo komunetako txikienak adierazten duen letra-kopurua izango du, salbuespenak izan ezik; batzuetan letra gutxiagoko gakoak ager baitaitezke.
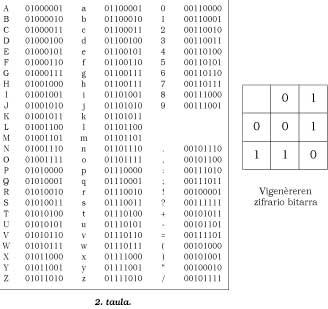
Zifrario-mota desberdinak ere osa daitezke. Ordenadoreekin ASCII kode ezaguna sortu zen (2. taula). Bertan 0 eta 1 zifrak soilik erabiltzen dira. Vigenèreren sistema erabiltzen badugu (13. irudia), honakoa lortuko dugu:
Mezua Æ ASCII Æ Vigenère Æ kriptograma

Ideia horretan oinarritzen da orain arte inork deskriptatu ez duen zifrarioa; DES (Data Encryption Standard) zifrarioa, alegia. IBM enpresak 1977an kaleratu zuen.
Vigenèreren zifrarioa oinarri hartuta, zorizko gakoa erabiltzen bada zifrario perfektua lortuko dugu. Ikus dezagun: zorizko gakoa bi eratan aukera daiteke: sistema bitarrean txanpon bat airera jaurtikiz edo 26 sektoreko gurpila (erruleta) erabiliz. Gakoak mezuak adina letra (zifra) izango du. Horrelako zifrarioei, gako berrerabiltezinezko zifrario deitzen zaie.
Tresna matematikoak pixkanaka sartu dira kriptografian. Beste arloetan bezala hemen ere eman dira teoremak. Kriptografia teoriko modernoaren sortzaileak, Claude Shannon-ek (1916), ondokoak eman zituen:
1. teorema
Gako berrerabiltezinezko zifrarioa hartzen badugu, kriptograma osatzen duten letren (edo zifren) segida guztiz zorizkoa da.
2. teorema
Gako berrerabiltezinezko zifrarioa hartzen bada, kriptogramak, berez, eta gakoaren faltan, ez du jatorrizko mezuaz informaziorik ematen.
Bigarren teoremak, gako berrerabiltezinezko zifrarioak perfektuak direla dio.
Ez ezazu pentsa, hala ere, kriptografiaren azken helburua lortu dugunik.
3. teorema
Zifrario perfektuan gakoak ezin du mezua baino laburragoa izan.
Hirugarren teoremak dioenez gako berrerabiltezinezko zifrarioak oso astunak, deserosoak eta garestiegiak dira maneiatzeko. Ondorioz, oso gutxitan erabiltzen dira.
Gaur egungo ikerkuntza kriptografikoak bi bide jorratzen ditu: zifrario sasiperfektuak eta gako ezaguneko kriptografia.
Lehenengoa, zorizko gako hutsen ordez zorizko itxura duten baina zorizkoak ez diren gakoak erabiltzean datza. Esaterako, π zenbakiaren hamartarrek hautazko batetik aurrera zorizko segidaren antza dute. Gero, zenbaki bikoitiak eta bakoitiak hurrenez hurren 0 eta 1 bihurtuz, gako bitarra lortuko da.
John von Neumann-ek (1903-1957), joko-teoriaren sortzaileak, beste bat eman zuen: 10 zifrako zenbaki bat, hazia, hartzen da; bere karratua kalkulatutakoan hiru bloketan banatzen da: azkeneko 5 zifrena, erdiko 10 zifrena eta hasierako 4 edo 5 zifrena; erdiko blokearen zenbakia ber bi egiten da eta erdiko aldea berriro aukeratu (14. irudia). Erdiko zifrekin sasizorizko segida lortzen da. Geroago frogatuko zen sistema horrek periodikotasuna izatearen akatsa zuela.
Gaur egun ordenadoreen bidez sasizorizko zifrak erraz sor daitezke. Zifra horiek maiz erabiltzen dira injinerutzan, fisikan, matematikan eta abarretan fenomenoak simulatzeko, baina kriptografian porrot egiten dute. Horretan da oraingo ikerkuntza; kriptografiara egokitutako sasizorizko zifrak sortzeko metodo berriak asmatzen, alegia.

Kriptologian mende honetan egin den ekarpen handiena dugu bigarren bidearen oinarria: zifratzeko gakoa ez dago ixilean gorde beharrik. Ideia hori RSA (R. Rivest, A. Shamir eta L. Adleman asmatzaileen izenak) zifrarioan ikus dezakegu. Zifrarioak bi gako ditu, bata zifratzeko, bestea deszifratzeko. Bigarrena P eta Q bi zenbaki lehen handiz osatuta dago, eta lehenengoa bion arteko biderkaduraz:
M = P x Q
Gogora dezagun bi zenbakien biderkadura berehala kalkula daitekeela. Aldiz, zenbaki baten zenbaki lehenen bidezko deskonposaketa ez dago gure esku.
RSA zifrarioaren egitura hauxe da:
- hartzaileak bi zenbaki lehen handi sortzen ditu eta biderkadura kalkulatzen du;
- bi zenbaki lehenak sekretuak dira eta deszifratzeko gakoa osatzen dute;
- bion arteko biderkadura, hartzailearen izenarekin batera, argitara ematen da gida batean. Biderkadura, hartzaileari zuzendutako mezuak zifratzeko erabiltzen den gako publikoa da;
- mezua bidali nahi duenak gidan aurkituko du hartzaileari dagokion gakoa;
- kriptograma hartzaileari igortzen zaio;
- kriptograma zenbaki lehen sekretuek osatutako gakoaren laguntzaz deszifratuko da.
Jakina, zenbakiak zenbaki lehenetan deskonposatzeko algoritmo azkarra aurkituko balitz, RSA-ren ospea galdu egingo litzateke. Hala ere, badirudi oso zaila dela.
Kriptografiak bide luzea egin du hasieratik gaur egungo RSA-ra heltzeko. Mezuak garraiatzeko amarruak, segadak eta hamaika arrisku pairatu dituztenak ezkutatu egin dira. Orain Kriptologiak bide lasaiagoak ibili behar ditu, baina ez horregatik zirrara gabeak.
Oharra: Taulak eta irudiak ongi ikusteko jo ezazu PDF-ra.

Gai honi buruzko eduki gehiago
Elhuyarrek garatutako teknologia




