Modélisation de l'invasion de guêpe noire
2021/03/01 Oscoz Villanueva, Inaxio - Fisikaria Iturria: Elhuyar aldizkaria

Diffusion de la guêpe noire en Europe
Bien que certaines sources affirment que cette espèce a été introduite en Europe en 2004, cet animal a été vu pour la première fois en 2005 à Nérac (Lot-et-Garonne, France) [5]. Apparemment, il est arrivé au port de Bordeaux sur un chargement apporté d'Asie, dans un conteneur en céramique. C'est pourquoi, soutenu par l'adéquation du climat et l'incapacité des espèces locales à les combattre, il a commencé à se développer rapidement et a été détecté dans 32 départements français pour 2009 [5].
Compte tenu des similitudes bioclimatiques entre le climat de la zone cantabrique de la péninsule ibérique et la zone établie par la guêpe en France, le croisement des Pyrénées par la guêpe asiatique n'était qu'une question de temps. Ainsi, en août 2010, la première guêpe de ce type a été trouvée dans la localité d'Amaiur (Baztan, Navarre). Depuis lors, ils sont apparus ailleurs dans la péninsule ibérique, principalement sur la côte nord [5].
Aujourd'hui, nous pouvons dire que cet insecte est installé dans de nombreux endroits de la péninsule ibérique, mais aussi dans de nombreux autres pays européens. Cette situation est aggravante par ses effets sur la biodiversité locale et, en particulier, sur les abeilles. Le manque de mécanismes de défense contre la guêpe noire provoque une diminution de la population des abeilles qui, outre leur influence sur l'apiculture, engendre d'autres dommages. En fait, l'abeille est le principal pollinisateur de plantes à fleurs, puisqu'elle pollinise 70% des fleurs, elle influence donc directement la production alimentaire. Étant ce processus de pollinisation irremplaçable, le travail de l'abeille a une énorme valeur écologique et économique [4].
Modèle de l'invasion
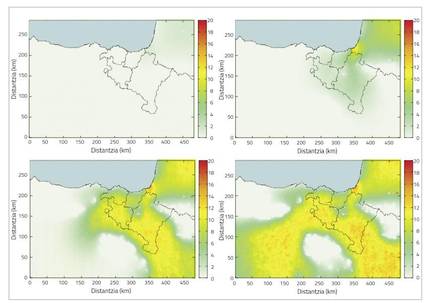
La voile Vespa est une population qui se développe rapidement et semble maintenir la même tendance. Comme nous l'avons déjà dit, cela pose un grave problème tant dans le domaine écologique que économique. Cependant, certaines mesures peuvent être prises pour combattre l'invasion. Mais pour cela, il faut bien connaître les caractéristiques de l'invasion (vitesse, extension, tendance…) pour créer avec elles un modèle qui modélise l'invasion.
Cependant, la dynamique d'expansion de la population présente deux caractéristiques de base. La première, l'expansion spatiale, qui indique la nature de l'expansion de la population. L'invasion a un seul foyer, qui dans ce cas serait le port de Bordeaux mentionné ci-dessus, par lequel il a été étendu. Il est facile d'imaginer que cette expansion a suivi la même tendance que celle d'un liquide, de sorte que l'expansion spatiale de l'invasion doit avoir certaines caractéristiques de la diffusion d'un liquide. La deuxième caractéristique fondamentale est la croissance intrinsèque de la population, qui fait référence au nombre total de guêpes. Malgré l'arrivée en Europe d'une seule colonie, il y a aujourd'hui des milliers et des milliers de colonies de guêpes. En principe, bien que cette croissance soit exponentielle, ce n'est pas toujours le cas. Si c'était toujours le cas, le nombre de guêpes augmenterait et augmenterait, vers une quantité infinie, et nous savons que cela ne peut pas être le cas parce que, comme les ressources d'un écosystème sont limitées, les individus qui le composent doivent être limités. Dans la pratique, la population se stabilise dans une certaine quantité, qui est considérée comme la valeur de la capacité maximale. L'équation qui explique le mieux la dynamique de propagation de ce type d'espèces envahissantes s'appelle l'équation de l'advection-difusion-réaction, souvent aussi appelée équation de diffusion. Cette équation des différentiels partiels fournit la densité de population (nombre d'individus par unité de surface) de l'espèce envahissante à chaque moment et lieu, expliquant les deux caractéristiques de base.
Bien sûr, comme dans les systèmes biologiques, il n'est pas possible de prédire avec certitude ce système, c'est-à-dire que nous nous trouvons face à un système indéterministe. Il faut donc ajouter un facteur aléatoire à notre modèle. En outre, il s'agit d'un système complexe dont les équations ne peuvent généralement pas être résolues analytiquement. Par conséquent, ce modèle doit être résolu par ordinateur. Le champ spatial et l'intervalle de temps que l'on souhaite étudier peut être drisketizar pour drisketiser notre équation d'adsorption diffusion et ensuite, avec la méthode dite de différences finies, avec l'aide d'un programme, simuler l'invasion. Cela permet d'obtenir la densité de population de la guêpe asiatique présente dans chaque lieu et moment. Cependant, avant de réaliser la simulation il est nécessaire de fixer quelques paramètres de l'équation. On utilisera donc les données partagées par la Députation Forale de Guipúzcoa et les informations obtenues à partir de divers articles, en faisant différentes approximations, pour fixer les paramètres de l'équation et les détails du système [3] [1].
En simulant ce qui précède, on obtient que la dynamique de base de l'expansion spatiale de l'invasion apparaisse d'une manière relativement adéquate. C'est-à-dire que les limites géologiques (densité nulle en mer et à des hauteurs supérieures à 1000 m de la mer) sont respectées et la vitesse de propagation est conforme à ce qui est observé dans la réalité. Cependant, la dynamique de croissance de la population ne se reflète pas du tout bien. Rappelons que ces paramètres ont été obtenus par des approches et des hypothèses diverses, qui peuvent ne pas être tout à fait adéquates. Pour améliorer ces paramètres, vous pouvez utiliser l'apprentissage statistique.
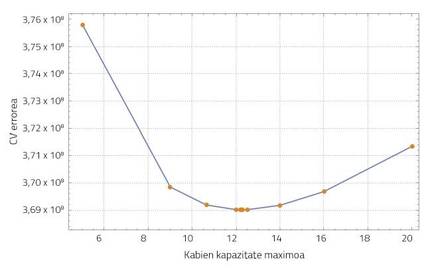
L'apprentissage statistique fait référence à un large éventail d'outils et de techniques de compréhension des données (en anglais, statistical learning) [6]. Dans ce cas, la méthode de validation croisée (cross-validation, CV) a été utilisée pour rechercher une valeur adéquate de la capacité maximale. Fondamentalement, la méthode CV proposera les valeurs de ce paramètre, en comparant le nombre de nids de guêpes à différents moments de la simulation dans tout Gipuzkoa avec le nombre de nids de guêpe détectés dans cette zone. La valeur de la capacité maximale qui rapproche le plus les résultats de la simulation aux données réelles est la plus appropriée, avec la moindre erreur de CV. Dans notre système, la densité de population de guêpe noire se stabilise à 12,24 nids/km².
La réalisation d'un modèle approprié d'invasion permet maintenant d'élaborer une stratégie de mesures qui peuvent être prises contre lui. Les mesures utilisées pour contrôler une espèce envahissante, dans ce cas la recherche et la destruction de nids, peuvent être très coûteuses. C'est pourquoi il est important d'envisager quelle est la stratégie la plus efficace. L'objectif est d'adopter des mesures qui éliminent l'espèce et minimisent les dommages à l'environnement, tout en minimisant les coûts de l'effort. Pour cela on utilise le champ des mathématiques appelé théorie du contrôle [2]. La recherche d'une stratégie optimale peut être très complexe, mais en substance, selon la théorie du contrôle, l'intensité des mesures pour ce type d'invasions doit être canalisée sur les bords de l'expansion de l'invasion. Par conséquent, au lieu d'appliquer les mesures de manière homogène dans l'espace, ils devraient être plus résistants sur les bords pour aller peu à peu « en arrière » l'invasion et ainsi pouvoir rendre plus efficaces les efforts de contrôle contre l'espèce.
Bibliographie Bibliographie

Gai honi buruzko eduki gehiago
Elhuyarrek garatutako teknologia






