Modelización da invasión de avispa negra

2021/03/01 Oscoz Villanueva, Inaxio - Fisikaria Iturria: Elhuyar aldizkaria

• Ingurumena
• Zoologia
• Biologia
• Ekologia

Difusión da avispa negra en Europa

A pesar de que algunhas fontes afirman que esta especie se introduciu en Europa en 2004, este animal viuse por primeira vez en 2005 en Nérac (Lot-et-Garonne, Francia) [5]. Ao parecer, chegou ao porto de Bordeus nun cargamento traído desde Asia, nun colector de cerámica. Por iso é polo que, apoiado pola idoneidade do clima e a incapacidade das especies locais paira combatelas, comezou a expandirse rapidamente e detectouse en 32 departamentos franceses paira 2009 [5].

Tendo en conta as similitudes bioclimáticas entre o clima da zona cantábrica da península Ibérica e a zona establecida pola avispa en Francia, o cruzamento dos Pireneos pola avispa asiática era só cuestión de tempo. Así, en agosto de 2010 atopouse a primeira avispa deste tipo na localidade de Amaiur (Baztan, Navarra). Desde entón foron aparecendo noutros lugares da península Ibérica, principalmente na costa norte [5].

Hoxe podemos dicir que este insecto está asentado en moitos lugares da península Ibérica, pero tamén noutros moitos países europeos. Esta situación resulta agravante polos seus efectos sobre a biodiversidade local e, en particular, sobre as abellas. A falta de mecanismos de defensa contra a avispa negra provoca una diminución da poboación das abellas que, ademais da súa influencia na apicultura, xera outros danos. De feito, a abella é o principal polinizador de plantas con flores, xa que poliniza o 70% das flores, polo que tamén inflúe directamente na produción de alimentos. Sendo este proceso de polinización insubstituíble, o traballo da abella ten un enorme valor ecolóxico e económico [4].

Modelo da invasión

Figura . Densidade niño (niño/km²) da avispa negra proporcionada polo simulacro en xuño 2012, xaneiro 2015, xuño 2017 e xaneiro 2020 respectivamente. Imaxes: Inaxio Oscoz.

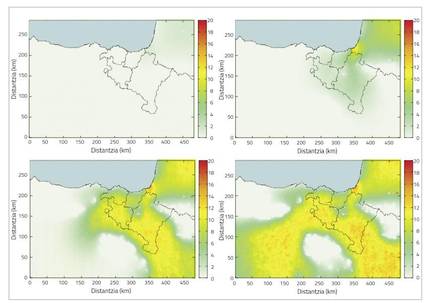
A velutina Vespa é una poboación que se expande rapidamente e parece que manterá a mesma tendencia. Como xa se comentou, isto supón un grave problema tanto no ámbito ecolóxico como no económico. No entanto, paira combater a invasión pódense tomar algunhas medidas. Pero paira iso é necesario coñecer ben as características da invasión (velocidade, extensión, tendencia…) paira crear con elas un modelo que modelice a invasión.

Con todo, a dinámica de expansión da poboación presenta dúas características básicas. A primeira, a expansión espacial, que indica a natureza da expansión da poboación. A invasión ten un único foco, que neste caso sería o porto de Bordeus antes mencionado, polo que se foi expandindo. É fácil imaxinar que esta expansión seguiu a mesma tendencia que a dun líquido, polo que a expansión espacial da invasión deberá ter certas características da difusión dun líquido. A segunda característica básica é o crecemento intrínseco da poboación, que fai referencia ao número total de avispas. A pesar da chegada a Europa dunha soa colonia, na actualidade hai miles e miles de colonias de avispas. En principio, aínda que este crecemento é exponencial, non sempre é así. Se sempre fóra así, o número de avispas iríase incrementando e aumentando, cara a unha cantidade infinita, e sabemos que isto non pode ser así porque, como os recursos dun ecosistema son limitados, os individuos que o compoñen deben ser limitados. Na práctica, a poboación estabilízase nunha cantidade determinada, que se considera como o valor da capacidade máxima. A ecuación que mellor explica a dinámica de propagación deste tipo de especies invasoras chámase ecuación de advección-difusión-reacción, a miúdo tamén denominada ecuación de difusión. Esta ecuación dos diferenciais parciais proporciona a densidade de poboación (número de individuos por unidade de superficie) da especie invasora en cada momento e lugar, explicando as dúas características básicas.

Por suposto, do mesmo xeito que nos sistemas biolóxicos, tampouco é posible predicir con certeza este sistema, é dicir, atopámonos ante un sistema indeterminista. Por iso, ao noso modelo hai que engadir un factor aleatorio. Ademais, trátase dun sistema complexo cuxas ecuacións normalmente non poden resolverse analiticamente. Por iso, este modelo debe resolverse computacionalmente. O campo espacial e o intervalo de tempo que se desexa estudar pódese drisketizar paira drisketizar a nosa ecuación de advección-difusión e posteriormente, co chamado método de diferenzas finitas, coa axuda dun programa, simular a invasión. Con iso conséguese a densidade de poboación da avispa asiática presente en cada lugar e momento. Con todo, antes de realizar a simulación é necesario fixar algúns parámetros da ecuación. Por tanto, utilizaranse os datos compartidos pola Deputación Foral de Gipuzkoa e a información obtida a partir de varios artigos, facendo diferentes aproximacións, paira fixar os parámetros da ecuación e os detalles do sistema [3] [1].

Simulando co anterior, conséguese que a dinámica básica da expansión espacial da invasión apareza dunha maneira relativamente adecuada. É dicir, respéctanse os límites xeolóxicos (densidade nula no mar e a alturas superiores a 1000 m do mar) e a velocidade de propagación axústase ao observado na realidade. Con todo, a dinámica de crecemento da poboación non se reflicte do todo ben. Lembremos que estes parámetros se obtiveron a través de aproximacións e suposicións diversas, que poden non ser do todo adecuadas. Paira mellorar estes parámetros pódese utilizar a aprendizaxe estatística.

Figura . Erros calculados polo método CV paira distintos valores da capacidade máxima dos niños en niño/km². Gráfico: Inaxio Oscoz.

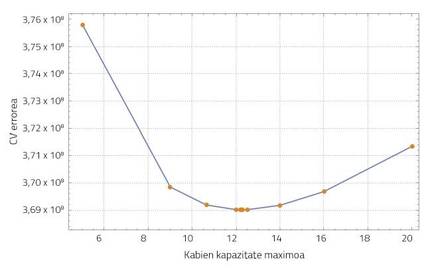
A aprendizaxe estatística fai referencia a un amplo abanico de ferramentas e técnicas de comprensión de datos (en inglés, statistical learning) [6]. Neste caso utilizouse o método de validación cruzada (cros-validation, CV) paira buscar un valor adecuado da capacidade máxima. Basicamente, o método CV irá propondo os valores deste parámetro, comparando o número de niños de avispas en diferentes momentos da simulación en toda Gipuzkoa co número de niños de avispa detectados nesta zona. O valor da capacidade máxima que máis achega os resultados da simulación aos datos reais é o máis adecuado, co menor erro de CV. No noso sistema a densidade de poboación de avispa negra estabilízase en 12,24 niños/km².

A consecución dun modelo adecuado de invasión permite agora elaborar una estratexia de medidas que poidan adoptarse na súa contra. As medidas que se utilizan paira controlar una especie invasora, neste caso a procura e destrución de niños, poden ser moi custosas. Por iso, é importante expor cal é a estratexia máis eficaz. O obxectivo é adoptar medidas que eliminen a especie e minimicen os danos ao medio ambiente, pero á vez minimicen os custos do esforzo. Paira iso utilízase o campo das matemáticas denominado teoría do control [2]. A procura dunha estratexia óptima pode ser moi complexa, pero en esencia, segundo a teoría de control, a intensidade das medidas paira este tipo de invasións debe canalizarse nos bordos da expansión da invasión. Por tanto, en lugar de aplicar as medidas de forma homoxénea no espazo, deberían ser máis resistentes nos bordos paira ir aos poucos “cara atrás” a invasión e así poder facer máis efectivos os esforzos de control contra a especie.

Bibliografía