Jocs sobre Lotus

1986/08/01 Goñi, Jesus Mari | Etxeberria, J. Iturria: Elhuyar aldizkaria

• Matematika

Com Alicia ens ha anat de vacances, aquesta vegada serà un altre tipus de joc el tema de la nostra obra.

En els últims mesos hem vist el començament de la implantació del joc de lotus en l'Estat. Res més posar-ho en marxa, la gent ho ha acceptat amb gran esperança. Revistes, periòdics… i altres publicacions estan plenes d'articles sobre lotus.

Aquests articles i apartats parlen d'un sistema curt, i encara que no es digui exactament, es tracta de convèncer als apostadors que existeixen diferents maneres d'omplir aquests bitllets, i que els números que sortiran són fàcilment accessibles.

Lotus és un joc d'atzar (aleatori) i els números que sortiran no hi ha forma adequada de predir.

Una vegada dit això, no us donarem la via adequada per a encertar els números i... de totes maneres, encara que tinguem aquest camí, no us el explicaríem. Enteneu per què?

No obstant això, volem fer uns petits estudis sobre el lotus. En primer lloc, quina probabilitat tenim d'inventar-nos els sis números quan juguem cinc vint-i-un?

Com sabem, la definició clàssica de probabilitat proporciona la probabilitat d'un esdeveniment A de la següent manera:

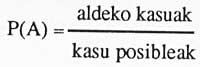
En la nostra aposta, els sis casos favorables són un. I… quants casos són possibles?

El problema no és difícil, perquè sabem que dels 49 números has de triar sis i encertar els sis.

I els possibles casos de sortida dels sis números diferents s'obtindran: Combinant grups de 6 en 6 amb aquests 49 números. És a dir, en un conjunt numèric de 49, tots els subgrups numèrics 6 seran:

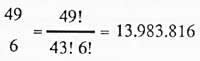
Per tant, la probabilitat d'encert és:

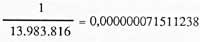
No ens ha sortit molt gran, no? Però, no obstant això, si assumim 200 milions? Bé, tots som adults i cadascun ho veurà.

A l'hora de realitzar els nostres càlculs hauríem de tenir en compte que el sistema de loteria de loteria de Lotus és el mateix que el de Nadal. Però si per Nadal es reparteixen com a màxim 100.000 números, en Lotus es reparteixen 13.983.816. El que canvia és, per descomptat, el lliurament de premis.

I no hem vist mai els sistemes abreujats que encara parlen de la loteria de nadal!

Ja que hem començat a parlar de Lotus, volem proposar-vos alguns maldecaps sobre aquest joc.

Aquests maldecaps són els realitzats després d'una conversa en el bar.

Allí estava xerrant diversos nens i per primera vegada escoltem:

No sé com vaig omplir aquesta targeta de lotus, però la setmana passada no vaig inventar cap número... després és difícil! No sé per què no concedeixen premis en aquests casos.

(1) Nosaltres: Quina és la probabilitat que cap número inventi?

Pello va dir: Jo crec que els nombres parells surten més. Mira la setmana passada, cinc dels sis números eren paris... La setmana que ve jo haig de posar tots paris.

(2) Nosaltres: Quina és la probabilitat que els sis números siguin paris?

El servidor també va participar i va dir:

La veritat és que els números acaben en xifres diferents. Si prenem els de la setmana anterior: Van finalitzar amb 2, 6, 3, 4, 0 i 8.

Nosaltres: Quina és la probabilitat que els 6 números acabin amb xifres diferents?

Com veiem, tots tenien alguna cosa a dir. José va arribar llavors i ell ens va tirar el següent.

En dues setmanes consecutives es repeteix almenys un número.

(4) Nosaltres: Quina és la probabilitat que ocorri el que ha dit Joxe?

(5) Finalment us expliquem aquest problema. Has de triar 6 números, però tenint en compte les següents condicions, i per descomptat, tens cinc vint-i-un números.

• Que no hi hagi número primer (primers)
• A l'hora de triar 6 números de Lotus, utilitzar 10 xifres i utilitzar cada xifra com a màxim una vegada.
• Una vegada seleccionat un número, no pot posar que estigui en les seves caselles contigües.
• L'última condició pot entendre's de dues formes.

Si les "caselles contigües" són d'un costat comú, nosaltres hem obtingut 6 resolucions.

Si les caselles contigües són aquelles que tenen un punt comú, nosaltres hem obtingut una única resolució.

Bé, ara queda a les vostres mans... Ah! i gastar poc!