Juegos sobre Loto

1986/08/01 Goñi, Jesus Mari | Etxeberria, J. Iturria: Elhuyar aldizkaria

• Matematika

Como Alicia nos ha ido de vacaciones, esta vez será otro tipo de juego el tema de nuestra obra.

En los últimos meses hemos visto el comienzo de la implantación del juego de lotos en el Estado. Nada más ponerlo en marcha, la gente lo ha aceptado con gran esperanza. Revistas, periódicos… y otras publicaciones están llenas de artículos sobre loto.

Estos artículos y apartados hablan de un sistema corto, y aunque no se diga exactamente, se trata de convencer a los apostantes de que existen diferentes formas de llenar esos boletos, y que los números que van a salir son fácilmente accesibles.

Loto es un juego de azar (aleatorio) y los números que van a salir no hay forma adecuada de predecir.

Una vez dicho esto, no os daremos la vía adecuada para acertar los números y... de todas formas, aunque tengamos ese camino, no os lo explicaríamos. ¿Entendéis por qué?

Sin embargo, queremos hacer unos pequeños estudios sobre el loto. En primer lugar, ¿qué probabilidad tenemos de inventarnos los seis números cuando jugamos cinco veintiún?

Como sabemos, la definición clásica de probabilidad proporciona la probabilidad de un evento A de la siguiente manera:

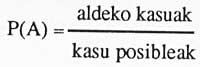
En nuestra apuesta, los seis casos favorables son uno. Y… ¿cuántos casos son posibles?

El problema no es difícil, porque sabemos que de los 49 números tienes que elegir seis y acertar los seis.

Y los posibles casos de salida de los seis números diferentes se obtendrán: Combinando grupos de 6 en 6 con estos 49 números. Es decir, en un conjunto numérico de 49, todos los subgrupos numéricos 6 serán:

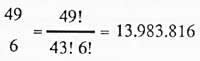
Por tanto, la probabilidad de acierto es:

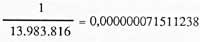
No nos ha salido muy grande, ¿no? Pero, sin embargo, ¿si asumimos 200 millones? Bueno, todos somos adultos y cada uno lo verá.

A la hora de realizar nuestros cálculos deberíamos tener en cuenta que el sistema de lotería de lotería de Loto es el mismo que el de Navidad. Pero si en Navidad se reparten como máximo 100.000 números, en Loto se reparten 13.983.816. Lo que cambia es, por supuesto, la entrega de premios.

¡Y no hemos visto nunca los sistemas abreviados que todavía hablan de la lotería de navidad!

Ya que hemos empezado a hablar de Loto, queremos proponeros algunos quebraderos de cabeza sobre este juego.

Estos quebraderos de cabeza son los realizados tras una conversación en el bar.

Allí estaba charlando varios niños y por primera vez escuchamos:

No sé cómo llené esta tarjeta de loto, pero la semana pasada no inventé ningún número... ¡luego es difícil! No sé por qué no conceden premios en estos casos.

(1) Nosotros: ¿Cuál es la probabilidad de que ningún número invente?

Pello dijo: Yo creo que los números pares salen más. Mira la semana pasada, cinco de los seis números eran pares... La semana que viene yo tengo que poner todos pares.

(2) Nosotros: ¿Cuál es la probabilidad de que los seis números sean pares?

El servidor también participó y dijo:

Lo cierto es que los números terminan en cifras diferentes. Si tomamos los de la semana anterior: Finalizaron con 2, 6, 3, 4, 0 y 8.

Nosotros: ¿Cuál es la probabilidad de que los 6 números terminen con cifras diferentes?

Como vemos, todos tenían algo que decir. José llegó entonces y él nos echó lo siguiente.

En dos semanas consecutivas se repite al menos un número.

(4) Nosotros: ¿Cuál es la probabilidad de que ocurra lo que ha dicho Joxe?

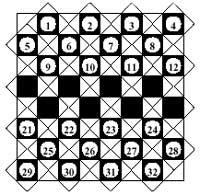
(5) Finalmente os explicamos este problema. Tienes que elegir 6 números, pero teniendo en cuenta las siguientes condiciones, y por supuesto, tienes cinco veintiún números.

• Que no haya número primero (primos)
• A la hora de elegir 6 números de Loto, utilizar 10 cifras y utilizar cada cifra como máximo una vez.
• Una vez seleccionado un número, no puede poner que esté en sus casillas contiguas.
• La última condición puede entenderse de dos formas.

Si las "casillas contiguas" son de un lado común, nosotros hemos obtenido 6 resoluciones.

Si las casillas contiguas son aquellas que tienen un punto común, nosotros hemos obtenido una única resolución.

Bueno, ahora queda en vuestras manos... ¡Ah! ¡y gastar poco!