Unha cartografía dos lugares onde se cruzan as matemáticas, a educación e o xénero

2024/10/23 Albizu Mallea, Uzuri - Euskal Herriko Unibertsitateko irakaslea eta ikertzailea Iturria: Elhuyar aldizkaria

• Sariak
• Berdintasuna
• Giza zientziak
• Matematika

En que medida a natureza da ciencia está ligada á idea de masculinidad? Esta pregunta foi lanzada polo físico e epistemólogo feminista Evelyn Fox Keller na década dos 80, no libro Reflections on gender and science. Para responder á pregunta, analizou algunhas formas históricas de caracterizar o coñecemento científico. A través da obra de Francis Bacon, por exemplo, demostrou que os roles de xénero e os estereotipos influíron de forma importante nas formas de caracterizar a ciencia da época. De feito, Bacon consideraba que a mente era masculina e a natureza feminina; afirmou que o coñecemento científico é o dominio da natureza e equiparou a relación entre a mente e a natureza cun matrimonio heterosexual. A análise do pensamento de René Descartes, pola contra, serviu para ver que as formas de caracterizar a ciencia tamén teñen un impacto nos sistemas de xénero. Descartes afirmou que o home está formado por dúas partes disxuntivas: a mente e o corpo. A dicotomía corpo mental deu lugar ao desenvolvemento de estereotipos moito máis extremos de masculinidad e feminidade, xa que a masculinidad asociouse coa mente e a feminidade co corpo e, sobre todo, co útero. Isto supuxo unha división sexual do traballo, que relegou ás mulleres ao ámbito reprodutivo.

Outros moitos epistemólogos feministas tamén puxeron de manifesto o carácter non neutral, androcéntrico e sexista da investigación científica. Os intentos por aflorar dinámicas de xénero dentro das matemáticas foron bastante inferiores. Aínda que poden ser varias as razóns, o alto grao de abstracción das matemáticas é probablemente unha das máis destacadas, xa que este carácter abstracto ha dado unha posición privilexiada tanto ao campo do coñecemento como á verdade matemática. Co fin de axudar a cubrir este buxán, indaguei na tese nas formas que adopta o xénero na educación matemática, a partir das vivencias, os discursos e as accións de matemáticos, profesores de matemáticas e alumnos de matemáticas.

Compases e coordenadas metodolóxicas

A tese é un estudo de caso. Analicei as matemáticas, a educación e as condicións nas que o xénero se cruza no día a día, tomando a aula como escenario principal. Aínda que o obxectivo é analizar con detalle a particularidade, a unicidad e a complexidade do caso, tamén fixen afirmacións máis xerais sobre o tema, seguindo o carácter instrumental da investigación. Nestes casos, é habitual que o estudo do caso único expoña dúbidas sobre as posibilidades que ofrece a análise para realizar afirmacións sobre un fenómeno máis xeral, debido á falta de recursos estadísticos utilizados nos deseños cuantitativos. Con todo, existen outras formas de reforzar a validez da investigación que se adaptan mellor aos deseños cualitativos.

Unha delas é a triangulación, unha forma de análise cruzada que permite contrastar e analizar os temas desde diferentes ángulos, así como reforzar as evidencias que hai detrás das afirmacións máis importantes. Na tese utilicei dous tipos de triangulación: triangulación de datos e triangulación metodolóxica. No que respecta á triangulación de datos, dirixinme a diferentes fontes de información, xa que tanto alumnos como profesores de matemáticas participaron na investigación. En canto á triangulación metodolóxica, utilicei diferentes técnicas e ferramentas para producir información: entrevistas en profundidade, cuestionarios abertos, pechos e mixtos, entre outros. Ademais, realicei máis de 200 horas de observación en tres aulas matemáticas. Tamén busquei a validación dos participantes para comprobar que están de acordo cos significados que lles deron ás súas palabras. Por último, valinme da teoría para profundar nas ideas producidas no proceso analítico, conceptualizar historias e dar forza ás miñas interpretacións.

Así, elaborei unha cartografía que informa dalgúns lugares nos que se cruzan as matemáticas, a educación e o xénero, unha interpretación enredada no presente, parcial e inacabada. Para dar a coñecer estes lugares esbocei catro percorridos (Figura 1) que resumirei nas seguintes liñas.

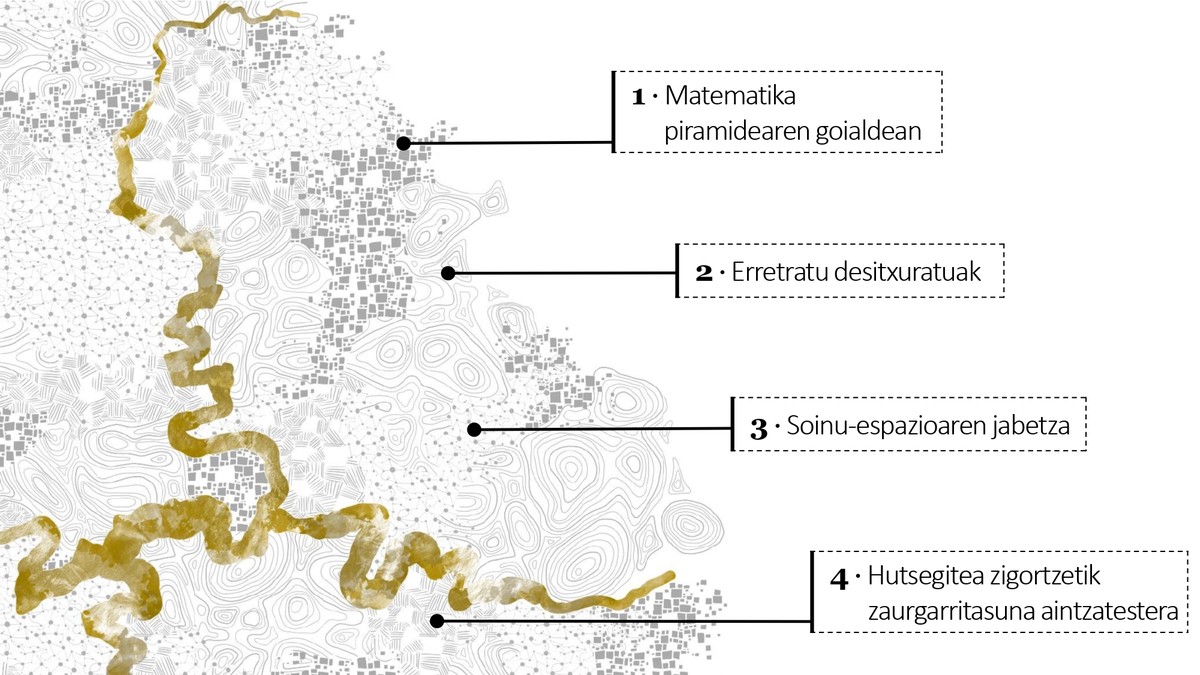
Primeiro percorrido: matemáticas na parte superior da pirámide

No último século, a matemática converteuse nun dos principais medios para defender os intereses das nacións. Desde a Segunda Guerra Mundial, o aumento do número de científicos, tecnólogos, enxeñeiros e matemáticos asóciase ao fortalecemento da economía e a seguridade nacional. Detrás deste empeño por estar á vangarda dos descubrimentos científicos e das innovacións tecnolóxicas, atópase a concepción moderna do progreso, que vincula o progreso económico e político co desenvolvemento científico e tecnolóxico. Esta actitude optimista cara á ciencia e a tecnoloxía levou precisamente a que a superioridade científica e tecnolóxica convértase na prioridade nacional de moitos países.

Esta centralidade da matemática na sociedade tamén inflúe na educación matemática, e na miña tese identifiquei algúns elementos que dan conta desa posición privilexiada da matemática na pirámide de áreas de coñecemento, entre os que se atopa o recoñecemento da importancia da matemática respecto doutras materias.

Por que ocorre isto? Pois porque as cualificacións matemáticas considéranse un indicador de éxito futuro e utilízanse para seleccionar e etiquetar aos alumnos. De feito, unha das funcións que se lle atribúen ás matemáticas é a de Medidor Mental. Ademais, a matemática é tamén apropiada para o talento académico, xa que a comunidade educativa trata de que os alumnos de alto rendemento académico elixan un itinerario relacionado coas matemáticas. Aos alumnos que non mostran un alto rendemento académico infórmaselles de que non son o suficientemente bos como para realizar estes estudos.

En consecuencia, a matemática desempeña unha función de segregación. Así mesmo, as tácticas de asimilación e repelencia da matemática fomentan a toma de decisións académicas en termos de destreza e o goce nun segundo plano. Ademais, se esencializa e dicotomiza o talento para as matemáticas: o talento para as matemáticas non é algo que se poida adquirir, senón algo que tes ou non tes desde o nacemento.

Segunda ruta: retratos distorsionados

A tese non caracteriza ao talento matemático desta forma dicotómica e esencialista. Pola contra, considérao unha construción ideolóxica e expón algúns elementos relacionados con devandita construción. Un destes elementos é o dos estereotipos de xénero que constrúen histórica e socialmente as características e actitudes diferenciadas, históricas e socialmente asignados aos homes e mulleres, naturalizando e biologizando as identidades hexemónicas de xénero, e fomentando as relacións discriminatorias entre xéneros.

Existen unha serie de estereotipos de xénero relacionados co ensino das matemáticas. Por exemplo, adóitase pensar que os mozos son por si mesmos mellores para as matemáticas e, doutra banda, téndese a valorar en exceso a capacidade dos mozos e a infravalorar a das mozas. Ademais, o éxito matemático das mozas asóciase ao esforzo e a obediencia, mentres que o dos mozos relaciónase coa intelixencia ou o interese. O fracaso atribúese no caso das mozas á falta de capacidade para entender as matemáticas, no dos mozos á mala relación co profesor ou á falta de axuda.

Na miña tese identifiquei varios fenómenos derivados destes retratos distorsionados. No caso do alumnado matemático, a performance de talento matemático adoita dar lugar a unha veracidade de xénero no caso dos nenos e a unha falsidade de xénero no das nenas. De feito, a presentación dun mesmo como un talento matemático coincide coa masculinidad hexemónica, pero choca coa feminidade hexemónica porque supón unha ruptura das normas de xénero. En canto á incidencia dos estereotipos de xénero no profesorado de matemáticas, un maior recoñecemento da autoridade formal aos homes que ás mulleres leva tamén un maior recoñecemento da autoridade epistémica aos homes. A incorporación dun profesor masculino á aula, por mor da súa propia configuración, permitirá que os alumnos e alumnas fáganlle máis caso que a unha muller, polo que poida que se lle recoñeza máis capacidade matemática que a unha profesora de matemáticas.

Terceiro percorrido: a propiedade do espazo sonoro

A participación na educación matemática, desde a perspectiva de xénero, é tamén un elemento problemático. Segundo os estudos, os alumnos e alumnas adoitan recibir máis axudas individuais, inician máis conversacións cos profesores e profesoras de matemáticas e dominan as conversacións que xorden no grupo grande. Ademais, teñen unha maior visibilidade, xa que os profesores aprenden e lembran máis facilmente os nomes dos mozos e facilitan a identificación do talento matemático dos mozos. Tamén se tende a unha distribución xeneralizada do traballo en equipo: as mozas realizan con máis frecuencia tarefas reprodutivas e non espectaculares, e os mozos participan máis en actividades que permiten mostrar unha actitude proactiva.

Para aumentar a participación das nenas, o profesor debe controlar as cotas de participación de maneira que o alumnado ocupe o espazo sonoro da maneira máis equilibrada posible. Ademais, o enfoque das relacións en grupos pequenos pode axudar a aumentar a sensación de participación do alumnado que non participa nun grupo grande. Ademais, é imprescindible que o profesorado se fixe en todo o que está a suceder nos grupos pequenos e interveña nas dinámicas excluíntes. Por último, é importante acordar unhas normas que se teñan en conta para o coidado mutuo ao traballar en grupos pequenos, de forma que todos os alumnos e alumnas sentan respectados e escoitados.

Cuarta ruta: da penalización da falta á valoración da vulnerabilidade

En matemáticas, fallar pode ter un maior impacto nas mozas que nos mozos. E é que as nenas aprenden desde pequenos para que as valoren e valórenas, deben ser educadas e humildes e respectar as normas, á vez que expresan perfección e beleza. Aos mozos acéptaselles o caos, o que lles prepara para estar na imperfección. En consecuencia, o fallo adoita provocar máis medo nas mozas que nos mozos.

O castigo do erro incita a ese medo, porque prexudica á confianza matemática. A competitividade tamén ten un impacto negativo, e nos relatos dos alumnos de matemáticas aparece frecuentemente relacionada coa ansiedade matemática. Iso é significativo desde o punto de vista de xénero, xa que cando o ambiente é competitivo a ansiedade matemática maniféstase máis nas nenas que nos nenos.

Para facer fronte a estas inercias, hai que facer unha xestión diferente do fracaso. Ofrecer ao alumnado experiencias positivas relacionadas co fallo, traballando a metacognición ou integrando o erro na actividade matemática, entre outros aspectos. De feito, dar cabida ao fracaso e pór a vulnerabilidade no centro pode axudar a combater o medo ao erro, os aspectos prexudiciais do perfeccionismo e os bloqueos.

Epílogo: unha cartografía que resalta a interdisciplinariedad en ouro

Esta investigación foi realizada por un matemático, pero non só polas matemáticas, senón que a didáctica das matemáticas e as aprendizaxes feministas foron tamén fontes de coñecemento fundamental. Por iso, na portada da tese, ademais das texturas que simbolizan as catro traxectorias superiores, existe unha trama dourada que pretende visibilizar esta interdisciplinaridad (Figura 1). A trama áurea simboliza a técnica kintsugi, unha forma de reparación de obxectos cerámicos que, no canto de disimular as gretas co po dourado, as gretas forman parte da historia dos obxectos e, por tanto, en lugar de escondelas, deberían ser mostradas e valoradas.

Ás veces, a técnica kintsugi consiste en xuntar fragmentos procedentes de diferentes lugares para formar algo novo. E esa é precisamente a tese: un intento de unificar os fragmentos que compoñen a miña traxectoria académica e profesional. Unha cartografía que resalta con ouro a interdisciplinariedad do traballo.

Bibliografía

[1] Negro, L., Mendick, H., Solomon, E. (editores). (2011). Mathematical relationships in education: Identities and participation. Routledge.

[2] Damarin, S. (2000). The mathematically able as a marked category. Gender and Education, 12(1), 69-85. https://doi.org/10.1080/09540250020418

[3] Faulkner, W. (2011). Gender (in)authenticity, belonging and identity work in engineering. Brussels Economic Review, 54(2/3), 277-293.

[4] Forgasz, H. J., Becker, J. R., Le, K. H., Steinthorsdottir, Ou. O doutor B. (editores) (2010). International perspectives on gender and mathematics education. Publishing Inc.

[5] Fox Keller, E. 1985). Reflections on gender and science. Yale University Press.

[6] Fulmer, G. (2014). Undergraduates’ attitudes toward science and their epistemological beliefs: Positive effects to certainty and authority beliefs. Journal of Science Education and Technology, 23(1), 198-206. https://doi.org/10.1007/s10956-013-9463-7

[7] Gates, P., e Vistro-Yu, C. (2003). Is mathematics for all? In Second international handbook of mathematics education (páxinas 31-73). Springer.

[8] Iriberry, N., e Rei-Biel, P. (2019). Competitive pressure widens the gender gap in performance: Evidence from a two-stage competition in mathematics. The Economic Journal, 129(620), 1863-1893. https://doi.org/10.1111/ecoj.12617

[9] Kollosche, D. (2018). Social functions of mathematics education: A framework for socio-political studies. Educational Studies in Mathematics, 98(3), 287-303. https://doi.org/10.1007/s10649-018-9818-3

[10] Ortega, L., Treviño, E., e Gelber, D. (2021) The inclusion of girls in Berran mathematics classrooms: Gender bias in teacher-student interaction networks. Journal for the Study of Education and Development, 44(3), 623-674. https://doi.org/10.1080/02103702.2020.1773064

[11] Zouda, M. (2018). Issues of power and control in STEM education: A reading through the postmodern condition. Cultural Studies of Science Education, 13(4), 1109-1128.