Mathematica (e IV)
1998/07/01 Angulo, Patxi | Lazkano, Elena Iturria: Elhuyar aldizkaria
4º Volume delimitado polas dúas superficies
- Enunciado
Calculamos agora o volume que delimitan ambas as superficies no espazo. Paira iso utilizaremos una dobre integral. Paira definir os límites das integrais, representaremos as proxeccións de superficies desde diferentes puntos de vista.
- Pasos da resolución
Primeiro calcularemos os extremos normais da función paira logo poder comparalos cos extremos condicionados. Calcularemos os extremos condicionados utilizando o método de multiplicadores de Lagrange.
- Instrucións a utilizar
- ParametricPlot3D: realiza un gráfico tridimensional a partir de ecuacións paramétricas. Utilízase paira representar superficies que non poden expresarse como funcións.
- ViewPoint: mostra a imaxe tridimensional desde un punto de vista concreto.
- DisplayFunction: permite visualizar o gráfico ou mantelo oculto.
- Show: mostrará os compoñentes gráficos.
- Graphics: converterá o dato que se lle dá nun elemento representable.
- Circle: con centro e radio representa a circunferencia.
- Disk: con centro e radio representa o círculo.
- Rectangle: representa o rectángulo cos vértices inferior esquerdo e superior dereito.
- RGBColor: cor da imaxe dun gráfico.
- Axes: característica de representar ou non os eixos dos gráficos.
- AspecRatio: característica de representar a proporción entre os eixos do gráfico.
- ViewPoint: mostra a imaxe tridimensional desde un punto de vista concreto.
- Integrate: calcula a integral. Mediante dúas variables, calcula o integral dobre.
- Simplify: simplifica una expresión algebraica.
%, fai referencia ao resultado anterior.
- Resolución por Mathematica
Ecuacións cartesianas:
esfera x2 + y2 + z2 = Cilindro 4: x2 + y2 - 2e = 0Ecuacións paramétricas:
esfera: | x = 2cos[t] cos[v], | cilindro: | x = 2sen[t] cos[t], |
| e = 2sen[t] cos[v], | e = 2sen[t]2, | ||
| z = 2sen[v], | z = z |
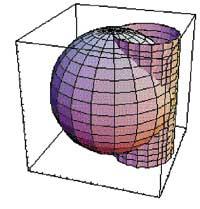
Imaxe tridimensional:
e = ParametricPlot3D[{2cos[t]cos[v], 2sen[t]cos[v], 2sen[v]}, {t,0,2ler}, {v,-cer/2,ler/2}, View>{3,1,1.5}, DisplayFunction <Identity]
-Graphics3D-
z = ParametricPlot3D[ {2sen[t]cos[t],2sen[t]2,z}, {t,0,2{}, {z,-2,2}, ViewPoint Regra {3,1,1.5}, DisplayFunction> Identity]
-Graphics3D-
Show[e, z, DisplayFunction: $DisplayFunction]
-Graphics3D-
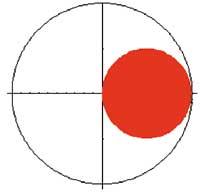
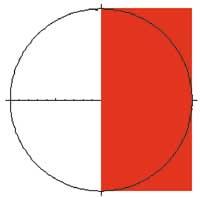
Proxección en planta:
pc=Graphics[{Circle[{0,0},2], {RGBColor[1,0,0], Disk[{1,0},1]}, Axes> True, AspectRatio Automatic]
-Graphics3D-
Show[xliff-newline]
-Graphics3D-
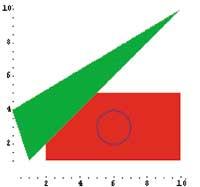
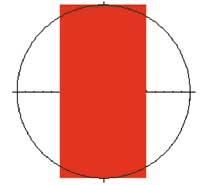
Proxección previa:
Abr=Graphics[{{RGBColor[1,0,0], Rectangle[{0,-2},{2,2}]}, Circle[{0,0},2]}, Axes- True, AspectRatio-Automatic]
-Graphics3D-
Show[abr]
-Graphics3D-
Proxección desde a dereita:
epr=Graphics[{{RGBColor[1,0,0], Rectangle[{-1,-2},{1,2}]}, Circle[{0,0},2]}, Axes> True, AspectRatio Regra Automatic]
-Graphics3D-
Show[epr, Axes> True]
-Graphics3D-
Integral dobre:
Límites de integrais en coordenadas cartesianas:
e Prudencio [0, 2],x Convén [-] (2 e - y2), » (2 e - y2)]integrado: z = » (4 - x2 - y2).Límites de integrais en coordenadas cilíndricas:
integrando
z = r * (4 - r2)Nota: con estes límites só calcularemos a metade superior do volume.
Integrate[r*Sqrt[4-r2],{t,0,{},{r,0,2sen[t]}]?8/3
+ 4/9 (-4 + 3ess) - 4/9 (4 + 3?)
Simplify[%]
8/9 (-4 + 3ler)
Isto é a metade superior do volume. Por tanto, o volume total:
2 * 16/9
(-4 + 3ash)
- Comentarios
Primeiro fixemos una imaxe tridimensional paira captar a idea de volume. Paira iso utilizamos as tradicionais ordes ParametricPlot3D e Show e eliximos o enfoque estándar a través da característica ViewPoint. A continuación, representamos as tres proxeccións de volume, a superior, a frontal e a dereita, utilizando as ordes Disk, Rectangle, Circle, Graphics e Show. Nela tamén aproveitamos DisplayFunction, RGBColor, AspectRatio e Axes. Por último, calculamos o integral dobre coa orde Integrate e simplificamos o resultado mediante Simplify. Desta forma conseguimos a metade do volume. O volume total obtense multiplicando o resultado anterior (%) por dous.

Gai honi buruzko eduki gehiago
Elhuyarrek garatutako teknologia