Mathematica

1998/04/01 Angulo, Patxi | Lazkano, Elena Iturria: Elhuyar aldizkaria

• Matematika

Para conocer algo de la historia, digamos que la primera versión de Mathematica salió en 1988 para los ordenadores Apple Macintosh, pero fue rápidamente desarrollada para su uso en otras plataformas: IBM PC, Silicon Graphics, Hewlett Paccard, Sun, etc… La segunda versión se lanzó en 1991 y ha sido la que se ha utilizado en los ordenadores hasta septiembre del año pasado, cuando finalizó la tercera versión: Mathematica 3.0. Son básicamente similares. La modificación más significativa es el conjunto de caracteres utilizados para expresar expresiones matemáticas ( mathematical typesetting ). Los nuevos símbolos matemáticos tienen un significado tipográfico y funcional. Por ejemplo, cada operación tenía su código o clave de palabra en versiones anteriores. En esta última versión, la mayoría de las operaciones se pueden expresar tanto por clave de palabra como por escritura matemática. Por ejemplo:

Power[2,10] o 210 Sqrt[28 ] o “w28

Al mismo tiempo, los ficheros creados por Mathematica versión 3.0 son expresiones propias de Mathematica, lo que permite manipularlos en programas como cualquier otra expresión simbólica. La capacidad de computación también es mayor en esta versión, con mayor velocidad de ejecución y menor memoria en algunas operaciones. También se han incorporado nuevas funciones y herramientas, y se han mejorado otras ya conocidas. Mencionar también que es necesario disponer de un ordenador majo suficiente para utilizar esta última versión de forma cómoda, ya que recomiendan 16 MB de Ram y 75 MB de disco duro. Para finalizar, indicar que todos los ejemplos que se van a exponer serán realizados con Mathematica versión 3.0.

Su principal ventaja es su capacidad para trabajar con expresiones simbólicas. “Cualquier cosa puede expresarse como simbólica expresiva”. Esa fue la idea básica de los que construyeron Mathematica. Por tanto, puede utilizarse como calculadora numérica o simbólica, sirve para visualizar datos y funciones, ofrece un lenguaje de alto nivel para escribir programas, es un entorno idóneo para el análisis de datos y, sobre todo, es una herramienta capaz de combinar texto, gráficos (si se desea animados) y fórmulas activas en documentos interactivos. También puede manejar el sonido, ya que permite definir objetos de sonido.

Mathematica puede realizar tres tipos de operaciones: numéricas, simbólicas y gráficas. En cuanto a la computación numérica, la forma más sencilla de utilizar Mathematica es utilizarla como calculadora. Sin embargo, las calculadoras tienen una precisión fija, es decir, el número de cifras decimales está fijado de antemano, mientras que en Mathematica se puede indicar en la propia orden la precisión requerida al cálculo. En el siguiente ejemplo los que están en negrita son los pedidos realizados a Mathematica y en letra simple las respuestas dadas por Mathematica (las palabras clave In:=[número] y Out=[número] que aparecen anteriormente son añadidas por el propio programa para diferenciar las entradas y salidas, relacionar cada salida con la entrada correspondiente y después hacer referencias a dichas entradas/salidas mediante un número sencillo).

l n[1]:=log[4Pi] Out[1]=log(4cer) l[2]:=n[Log[4ler]] Out[2]=2.53102 ln[3]:=n[Log 4cer],10] Out[3]=2.531024247

Por otra parte, el conjunto de operaciones es mayor, unas 750 funciones de integral elíptica y Bessel, incluyendo la factorización de funciones hipergeométricas y números enteros.

También puede aplicar operaciones numéricas como integración numérica, programación lineal, etc. Además, proporciona soluciones a ecuaciones algebraicas y a ecuaciones diferenciales convencionales.

Entre las computaciones simbólicas que realiza destaca la manipulación de fórmulas algebraicas. El polinomio y la expresión racional pueden simplificarse, extenderse o factorizarse. También puede encontrar soluciones algebraicas de ecuaciones polinomiales y sistemas de ecuaciones. A diferencia de la segunda versión, en la última versión incorpora facilidades para trabajar con matrices y no es obligatorio el uso de tablas para la definición de matrices.

Asimismo, evalúa simbólicamente las integrales y sus derivados, manejando aproximaciones por series y calculando límites.

En el campo de los gráficos, realiza gráficos bidimensionales y tridimensionales, plots densidad y contour (visiones superiores), tanto desde funciones como desde listas de datos. Además, existen numerosas posibilidades de controlar los detalles del gráfico, p.ej. : enfoque, color, luminosidad…

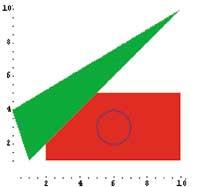
Dispone de una biblioteca para gráficos predefinidos, que mediante una serie de órdenes primitivas de objetos geométricos (por ejemplo, polígonos) muestra los objetos gráficamente mediante una representación simbólica.

} rectángulo = Graphics[{RGBColor[1,0,0], Rectangle[{2,1}, 10, 5}] rectángulo = Graphics[{RGBCcolor[1,0,0], Angle[{2,1}, {10, 5}]> Graphics

•Graphics•

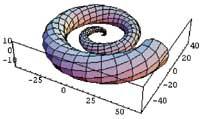
Todos los gráficos formados por Mathematica tienen formato PostScript (PS) por lo que pueden ser transportados a otras aplicaciones.

ParametricPlot3D[{uCos[u] (4+Cos[v+u]), uSin[u] (4+Cos[v+u]), uSin[v+u]}, {u,0,4>}, {v,0,2>}, PlotPoints > {60,12}]

Además, tiene un lenguaje propio, por lo que se pueden escribir programas en el lenguaje Mathematica.

Por otra parte, el lenguaje de programación Mathematica admite diferentes estilos de programación: procedimental, con estructura de bloques, órdenes condicionales y flejes repetitivos; funcional, con agentes funcionales; programación basada en reglas, equiparación modal ( pattern matching ) y programación orientada a objetos.

El programa Mathematica se estructura en dos grandes partes: el kernel y el front-end. Kernel es el núcleo, la parte encargada de realizar los cálculos, y el front-end es sólo la parte que interacciona con el usuario, una interfaz cómoda para el usuario y cuyas órdenes son enviadas al kernel. Si el kernel es el mismo en todas las plataformas de ordenador, podríamos encontrarlo con diferentes front-end, que se ha optimizado para ciertas arquitecturas. Este front-end ofrece al usuario documentos denominados “notebook”, es decir, texto escalonado por prioridad, gráficos animados y expresiones matemáticas (fórmulas, etc.) Cuadernos que admite. En estos cuadernos se puede elaborar material pedagógico o de otro tipo, y la característica más singular es que, además de las explicaciones escritas, se pueden realizar operaciones en los mismos.

En general, Mathematica se caracteriza por su compatibilidad comunicativa con otros muchos programas. Esto le permite leer datos en diferentes formatos (C, Fortran, TEX). Al utilizar el estándar MathLink, puede intercambiar datos y comandos con otras aplicaciones.

Durante la ejecución del mathematica se cargan algunas bibliotecas estardíes. En ellas se incluyen funciones básicas de cálculo matemático, gráficos y otras áreas matemáticas comunes. Sin embargo, Mathematica también dispone de otras bibliotecas más específicas que no se cargan cuando se inicia el programa. La carga de los mismos o de los Packages definidos para sus necesidades específicas está a disposición del usuario. Por ejemplo, supongamos que hemos definido las funciones “factorial” y “exponencial” en la librería “gurelib”.

DeclarePackage[“Calculus`gurelib`”,{”factorial”,”exponencial”}]

una vez ejecutada la orden, podremos utilizar las operaciones factorial y exponencial según la norma de orden dada en la definición. La biblioteca que Mathematica tiene cargada en cada momento se guarda en la variable global $Packages.

Como no podía ser de otra manera, Mathematica también tiene su propia dirección Web, donde se pueden encontrar información, gráficos y últimas noticias: http://www.wolfram.com