Maurits Cornelis Escher (and III)

1992/04/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

Impossible worlds

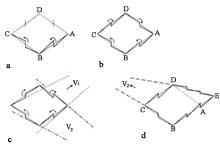
He also addressed the issue of impossible worlds. Before mentioning some images, let us analyze with an example the essence of them (Figure 1). In the image you can see a diamond and a square stuck and all the images are equal except the shadow. The upper and lower figures can be understood in two forms, as indicated in them. The same goes for everything we see. What happens is that many details we see without realizing it have an unmistakable interpretation. Without them the angle of incidence of light generates different interpretations.

Figure .

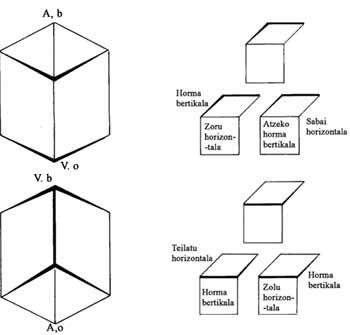
In the concave and convex image, the ogival cubic temples form the most important architectural element [1]. That is why we have represented the adjacent cubes with two interpretations (Figure 2). As soon as it is seen, the symmetry of the image is appreciated; the central filtering is not abrupt, but staggered. But after half, the top becomes low and the front becomes back. Humans, lizards and parrots, on the other hand, face investment. However, if they wanted to change parts (from left to right or vice versa) they would pay expensive. For example, if the one who is climbing the stairs in the lower left would like to turn around the temple, pass in front of the sit-in, pass the central shell and climb the stairs in front, he would be frightened to realize that the staircase at his feet has become a roof. The same would happen to all the characters on the left.

The vault between the two dulzaineros is surprising. While for the one on the left is the roof, that is, he can jump, for the one on the right the roof is the roof, that is, if he jumped it would fall to the ground.

Figure 2 has divided the picture into four parts. The left side has a convex architecture, as if we could see all the points from above. On the right is used concave architecture, that is, we see everything from below. In the two central parts the interpretation is double, apart from humans, lizards and parrots.

Every image of reality is a projection on the flat surface of that reality. Any figure of a launa surface does not have to be the projection of three-dimensional reality. This is the case of Belvedere, 1958, in lithography, which gives us the solution of the painting itself [2]. The key is that kind of cube that the boy who appears sitting on it has (Figure 3). Let's look at the adjacent cubes. In the first we have two options, depending on the vertices 1 and 4 being more or less close to us than the vertices 2 and 3. Likewise, vertices 2 and 4 could be seen closer than the rest, despite contravening our idea of cube in our mind. If we give volume to the edges of the cube, among other things, we could get “buckets” b and c, against what our senses have (figure 4).

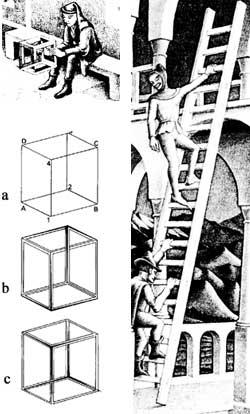
In Belvedere we can see both the interior and exterior staircase. The direction of the longitudinal axis of the upper floor is what the woman sees. The one below, that of man, which forms a right angle. The columns that connect the first and second floors, except those of the ends, join the front and back sides, that is, they are diagonal and not vertical. The image can be divided horizontally into two, with the upper and lower right parts (buildable). However, both cannot exist simultaneously.

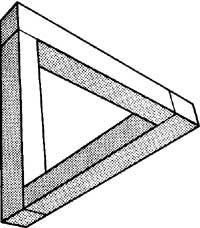
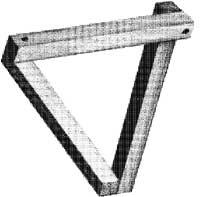
R. represented in figures 5 and 6. The lithograph Cascada de Escher (1961) was suggested by Penrose’s “tribar”. The tribar, like the previous cubes, cannot be built in three dimensions. If in “Salto de agua” we look only at the water, starting with turtuco, along the canal, the water is moving to the right, then to the left, to the right again and finally to the left, to go out to the Turkish. This tribar and water jump produce the same effect (Figure 7).

It was based on another image of Penrose for the lithograph of the Escher Staircase, above, below, 1960 (Figure 8). In this image he wanted to explain the idea of infinity. For this purpose the staircase that always goes up (or down) of Penros was used. If we follow the characters that are outside, even if we always go up, after a full tour we will realize that they are in the same place. The trap is exposed if we cut the building in horizontal saws. The first layer is at a lower level than the rest, that is, the layers are not overlapping, but form a spiral.

Figure 9 shows, horizontally, how a ladder can be obtained in continuous ascent (9 a, c). But this solution has a problem. _{Perspective is lost, as the escape points, V1 and V2,} remain under baptism. This can be resolved by lengthening to two sides (9 d). Escher's drawing tells us that this solution is valid.

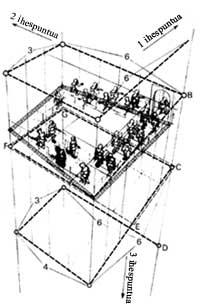
We know how the image deceives us: the staircase is located in a horizontal plane, while the rest of the details of the image (plinths of columns, window frames, etc.) forward in the form of a spiral. If we draw vertical lines at each level, we observe that these lines form a prism of proportions 6:6:3:4. All points in the image at the same height form a spiral (dot line) (Figure 10).

Approach to infinity

In an article written in 1959, Escher literally affirmed what motivated him to represent infinity: “It is impossible to think that there is nothing beyond the farthest stars we see on the horizon. (…). Therefore, since man is on the ground (standing, sitting or lying, running, sailing, riding and flying), beyond the presence of purgatory, heaven and hell, we maintain the idea of transmigration and mine, all of them spaces of infinite width or states of infinite duration in time”.

With the regular partition of the surface the infinite has not yet been achieved, but only part of it. But Escher's ability in regular surface partition proved very useful to him. However, a new element was needed: a structure that would represent the infinite surface on a finite surface.

In 1937 he made his first session using congruent images. In 1939 he used uniform images, but the idea of metamorphosis continued to predominate. Only since 1955 he used uniform images to form series that suggest infinity. These works can be divided into three sections, depending on the structure below the image: square images, spiral images and images suggested by Coxeter.

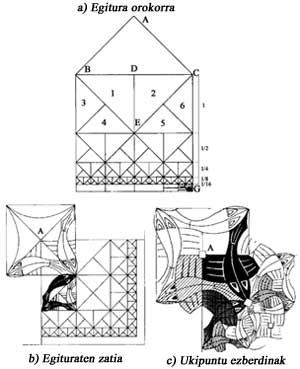
Figure 11 a shows a solution to the problem of representation of infinity. If the difference of the square EFCD is 10 cm, the bottom will be 5 cm, and the next 2.5 cm, etc. CG 20 cm, but we can see infinite squares smaller and smaller. Escher used this structure to illustrate a manual on regular surface partition.

Square limit, 1964, wooden drawing, with a more complex structure [3], but based on the previous one (Figure 11 b). To better understand the image, once the infrastructure is known, we will explain why three colors appear. Observing the points where the fish are touched, we will observe that they are of three types (Figure 11 c). At point A four fins of four fish are collected, at point B four heads and four tails, and at point C three fins. In points A and B no more than two colors are needed. In point C three colors are necessary. Points A are only in diagonals. Finally, the colors collected in points A and B appear in different combinations.

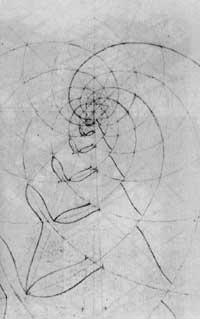
The structure below the spiral figures is a logarithmic spiral. This mathematical concept was not known by Escher and he discovered it in the following way (Figure 12): it represented the first concentric circles, decreasing the distances between them towards the center. Then he traced the radii that divided the circles into the same arches. Starting from a point of the outer circumference, he marked the points that cut the radii and the circles so that once united they formed the spiral.

His life trajectory I, 1958, employed a double spiral that started from 8 points of the circumference. In Vital Path II, 1958, the starting points are four and in Vital Path III, 1966, twelve spirals start from 6 points.

The life path II shows that two spirals starting from two different points of the circumference are attached from the outside. Thus, you can reach the center from the outer boundary and then return to the starting point (Figure 13). In the image you can see the red spiral towards the center and the blue spiral coming out of the center, coinciding on its outside.

In Ubila, 1957, the drawing was prior to the life cycle and had not exhausted all possibilities [4]. In the upper and lower areas there are two spirals that move in the same direction. Spirals have been drawn on the back of two fish in the opposite direction. Only two printing plates have been used. For the representation of the upper grey and red fishes the two red and grey lower fishes have been used.

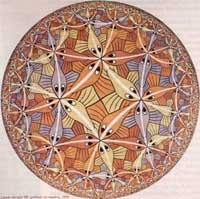
To represent the circular limit series, Escher H. It was based on the model used by mathematician Poincare to represent parabolic geometry. Model HSM He found it in a book by Coxeter (figure 14). Thus was born the circular Limit of 1958 I (little work). In Circular Limit II, similar to the previous one, it replaced the fish with crosses. The circular limit IV, 1960, is also based on the image of Coxeter. Instead, Circular Limit III, 1959 modified the infrastructure [5]. According to Escher himself: “The mistakes of the former have been eliminated as far as possible. On this occasion, all the fish in a series have the same color and go after the baptism, which grow as they approach the center. (…). No component affects the limit ....

The snake, 1969, drew in wood before suffering a complicated operation [6]. Despite being 71, the hand did not vibrate in his last work. In the dispute to express the infinite one can appreciate a greater humility (in the previous figures, with the help of a magnifying glass, he drew figures that measured less than half a millimeter). The snake did not end the series of small rings.

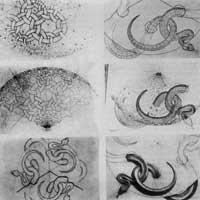
When he suggested a continuous decline in size he abandoned it (Figure 15). In the sketches we perceive Coxeter's infrastructure from the big rings out. But it gets the same effect inward, creating a wavy line. Snakes, after seeing many photos, represented them by heart. Previous studies highlight Escher's neatness for every detail. That was one of Escher's characteristics.

We have seen Escher's life and work. He used many mathematical structures unknowingly. That's why we brought this illustrator to this section. Although Escher died 20 years ago, he left us his job. Enjoy them!