Maurits Cornelis Escher (et III)

1992/04/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

Mondes impossibles

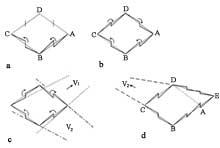
Il a également abordé le thème des mondes impossibles. Avant de mentionner quelques images, analysons avec un exemple l'essence de ces images (figure 1). Sur l'image vous pouvez voir un losange et un carré collés et toutes les images sont égales sauf l'ombre. Les figures supérieure et inférieure peuvent être comprises de deux manières, comme indiqué dans elles. Il en va de même pour tout ce que nous voyons. Ce qui se passe, c'est que beaucoup de détails que nous voyons sans nous rendre compte ont une interprétation unique. Sans eux, l'angle d'incidence de la lumière génère différentes interprétations.

Figure .

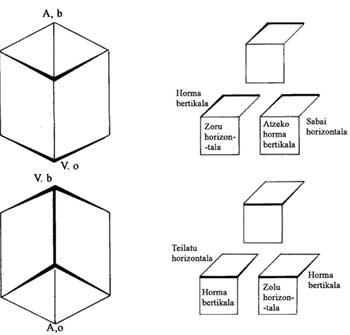
Dans l'image concave et convexe, les temples cubes ogivaux forment l'élément architectural le plus important [1]. C'est pourquoi nous avons représenté les cubes adjacents avec deux interprétations (figure 2). Dès que l'on voit la symétrie de l'image, le filtrage central n'est pas brusque, mais échelonné. Mais après la moitié, la partie supérieure devient basse et l'avant devient arrière. Les êtres humains, lézards et lorapotes, pour leur part, sont confrontés à l'investissement. Cependant, s'ils voulaient changer de partie (de gauche à droite ou vice versa) ils payeraient cher. Par exemple, si celui qui monte par l'escalier en bas à gauche voulait faire le tour du temple, passer devant le sit-in, passer la coquille centrale et monter par les escaliers devant, il aura peur en réalisant que l'escalier qui était à ses pieds est devenu un toit. La même chose se passerait à tous les personnages qui sont sur la gauche.

La voûte située entre les deux douceurs est surprenante. Tandis que pour celui de gauche est le toit, c'est-à-dire il peut sauter, pour celui de droite le plafond est le plafond, c'est-à-dire s'il sautait il tomberait jusqu'au plancher.

La figure 2 a divisé le tableau en quatre parties. La partie gauche a une architecture convexe, comme si nous pouvions voir tous les points d'en haut. Sur le côté droit est utilisé l'architecture concave, c'est à dire, nous voyons tout de bas. Dans les deux parties centrales, l'interprétation est double, en marge des humains, des lézards et des lorapotes.

Toute image de la réalité est une projection sur la surface plane de cette réalité. Toute figure de surface de l'une ne doit pas être la projection de la réalité tridimensionnelle. C'est le cas de Belvedere, 1958, dans la lithographie, que nous donne la solution le tableau lui-même [2]. La clé est dans cette sorte de cube qui a le garçon qui apparaît assis dessus (figure 3). Voyons les cubes adjacents. Dans la première, nous avons deux options, selon que les sommets 1 et 4 sont plus ou moins proches de nous que les sommets 2 et 3. De même, les sommets 2 et 4 pourraient être plus proches que le reste, même si cela contrevenait à notre idée de cube dans notre esprit. Si nous donnons du volume aux bords du cube, entre autres choses, nous pourrions obtenir “cubes” b et c, contre ce que nos sens ont (figure 4).

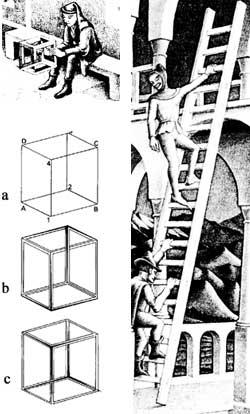
A Belvedere, nous pouvons voir à la fois l'escalier intérieur et extérieur. La direction de l'axe longitudinal de l'étage supérieur est celle que voit la femme. Celle d'en bas, celle de l'homme, qui forme un angle droit. Les colonnes qui relient le premier et le deuxième étage, sauf celles des extrémités, relient les côtés antérieur et postérieur, c'est-à-dire, sont en diagonale et non verticales. L'image peut être divisée horizontalement en deux, les parties supérieures et inférieures étant droites (modifiables). Cependant, les deux ne peuvent pas exister simultanément.

R. représentées dans les figures 5 et 6. La lithographie Cascade d'Escher (1961) a été suggérée par «tribar» de Penrose. La tribarre, comme les cubes précédents, ne peut pas être construite en trois dimensions. Si dans “Saut d’eau” on regarde seulement l’eau, en commençant par le turtuc, le long du canal, l’eau s’éloigne vers la droite, puis vers la gauche, vers la droite de nouveau et enfin vers la gauche, pour sortir au turc. Ce tribar et saut d'eau produisent le même effet (figure 7).

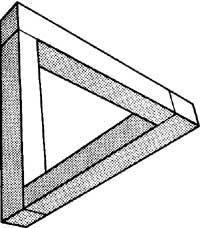
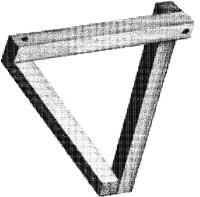
Il s'est appuyé sur une autre image de Penrose pour la lithographie de l'Escalier d'Escher, haut, bas, 1960 (Figure 8). Dans cette image, il a voulu expliquer l'idée de l'infini. Pour cela, nous avons utilisé l'escalier qui monte toujours (ou descend) de Penros. Si nous suivons les personnages qui sont à l'extérieur, même si nous montons toujours, après un tour complet, nous réaliserons qu'ils sont au même endroit. Le piège est découvert si nous coupons le bâtiment en scies horizontales. La première couche se trouve à un niveau inférieur au reste, c'est-à-dire que les couches ne sont pas superposées, mais forment une spirale.

Dans la figure 9, on peut observer, horizontalement, comment on peut obtenir un escalier en montée continue (9 a, c). Mais cette solution a un problème. Les points d'échappement, V1 et V2, restent sous le baptême. Cela peut être résolu si elle s'allonge sur deux faces (9 d). Le dessin d'Escher nous indique que cette solution est valide.

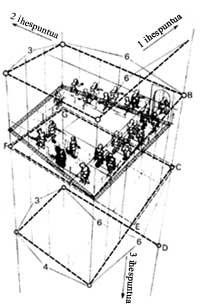
Nous savons comment l'image nous trompe : l'échelle se trouve sur un plan horizontal, tandis que les autres détails de l'image (plinthes de colonnes, cadres de fenêtres, etc.) Elles sont avancées sous forme de spirale. Si nous traçons droites verticales à chaque niveau, nous observons que ces lignes forment un prisme de proportions 6:6:3:4. Tous les points de l'image situés à la même hauteur forment une spirale (ligne de point) (Figure 10).

Approche à l’infini

Dans un article écrit en 1959, Escher a littéralement affirmé ce qui motivait à représenter l'infini: « Il est impossible de penser qu’il n’y a rien au-delà des étoiles les plus lointaines que nous voyons à l’horizon. (…). C’est pourquoi, depuis que l’homme est sur le sol (debout, assis ou couché, il court, navigue, va à cheval et il vole), au-delà de la présence du purgatoire, du ciel et de l’enfer, nous gardons l’idée de la transmigration et de la mienne, tous des espaces d’infinie largeur ou des états d’infinie durée dans le temps”.

Avec la partition régulière de la surface n'a pas encore obtenu l'infini, mais seulement une partie de celui-ci. Mais la capacité d'Escher sur la partition régulière de la surface a été très utile. Cependant, un nouvel élément était nécessaire : une structure qui permettrait de représenter la surface infinie sur une surface finie.

En 1937, il réalise sa première session à l'aide d'images congruentes. En 1939, il utilisa des images uniformes, mais l'idée de la métamorphose continuait à prédominer. Seulement depuis 1955, il a utilisé des images uniformes pour former des séries qui suggèrent infini. Ces travaux peuvent être divisés en trois sections, en fonction de la structure sous l'image: images carrées, images spirales et les images suggérées par Coxeter.

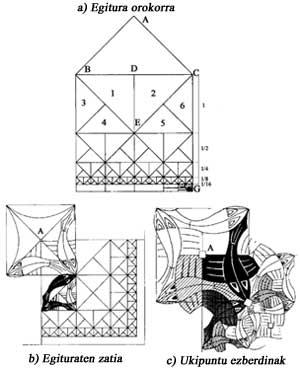
La figure 11 montre une solution au problème de représentation de l'infini. Si la différence du carré EFCD est de 10 cm, la partie inférieure sera de 5 cm, et la suivante de 2,5 cm, etc. CG 20 cm, mais nous pouvons voir des carrés infinis de plus en plus petits. Escher a utilisé cette structure pour illustrer un manuel sur la partition régulière de la surface.

Limite carrée, 1964, dessin en bois, avec une structure plus complexe [3], mais basée sur la précédente (Figure 11 b). Pour mieux comprendre l'image, une fois l'infrastructure connue, nous expliquerons pourquoi trois couleurs apparaissent. En observant les points sur lesquels les poissons se touchent, on remarquera qu'ils sont de trois types (figure 11 c). Au point A sont recueillies quatre nageoires de quatre poissons, au point B quatre têtes et quatre queues, et au point C trois nageoires. Les points A et B ne nécessitent pas plus de deux couleurs. Au point C trois couleurs sont nécessaires. Les points A sont seulement en diagonales. Enfin, les couleurs recueillies aux points A et B apparaissent dans différentes combinaisons.

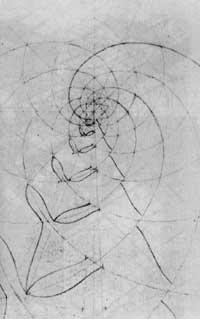
La structure sous les figures des spirales est une spirale logarithmique. Ce concept mathématique ne connaissait pas Escher et l'a découvert comme suit (Figure 12): il a représenté les premières circonférences concentriques, en diminuant les distances entre elles vers le centre. Il traça ensuite les rayons qui divisaient les circonférences dans les mêmes arcs. Partant d'un point de la circonférence extérieure, il a marqué les points qui coupent les rayons et les circonférences pour qu'une fois unis ils forment la spirale.

Son chemin de vie I, 1958, a employé la double spirale partant de 8 points de circonférence. En Trajectoire vitale II, 1958, les points de départ sont quatre et en Trajectoire vitale III, 1966, douze spirales partent de 6 points.

La trajectoire vitale II montre que deux spirales partant de deux points différents de la circonférence sont reliées de l'extérieur. Ainsi, vous pouvez atteindre le centre de la limite extérieure et de là revenir au point de départ (figure 13). Sur l'image, vous pouvez voir la spirale rouge vers le centre et la spirale bleue qui sort du centre, correspondant à son extérieur.

À Ubila, 1957, le dessin était antérieur au cycle de vie et n'avait pas épuisé toutes les possibilités [4]. Dans les zones supérieure et inférieure apparaissent deux spirales qui se déplacent dans la même direction. Les spirales ont été dessinées sur le dos de deux poissons dans le sens inverse. Seuls deux plaques d'impression ont été utilisées. Pour la représentation des poissons gris et rouges supérieurs, les deux couches de poissons inférieurs rouges et gris ont été utilisées.

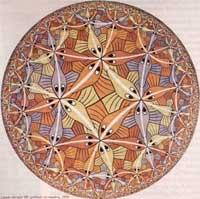
Pour représenter la série de limite circulaire, Escher H. Il a été basé sur le modèle utilisé par le mathématicien Poincare pour représenter la géométrie parabolique. Modèle HSM Il l'a trouvé dans un livre de Coxeter (figure 14). Ainsi naquit la Limite circulaire de 1958 I (peu de travail). Dans Limite circulaire II, semblable à la précédente, il a remplacé les poissons par des croix. La limite circulaire IV, 1960, est également basée sur l'image de Coxeter. En revanche, Limite circulaire III, 1959 a modifié l'infrastructure [5]. Selon Escher lui-même: « Les erreurs du premier ont été éliminées autant que possible. À cette occasion, tous les poissons d'une série ont la même couleur et vont après le baptême, ils grandissent à mesure qu'ils approchent du centre. (…). Aucun composant n'affecte la limite ....

Le serpent, 1969, a dessiné sur du bois avant de subir une opération compliquée [6]. Malgré 71 ans, la main n'a pas vibré dans son dernier travail. Dans le différend d'exprimer l'infini, on voit une plus grande humilité (dans les figures précédentes, à l'aide d'une loupe, il dessine des figures mesurant moins d'un demi-millimètre). Le serpent n'a pas fini avec la série de petits anneaux.

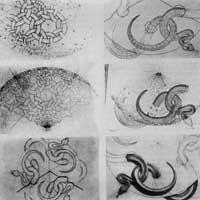
Lorsqu'il a suggéré une diminution continue de la taille, il l'a abandonné (Figure 15). Dans les croquis, nous percevons l'infrastructure de Coxeter à partir des grandes anneaux. Mais il obtient le même effet vers l'intérieur, créant une ligne ondulée. Les serpents, après avoir vu de nombreuses photos, les représentaient en mémoire. Des études antérieures montrent la propreté d'Escher pour chaque détail. C'était l'une des caractéristiques d'Escher.

Nous avons vu la vie et le travail d'Escher. Il a utilisé de nombreuses structures mathématiques sans le savoir. C'est pourquoi nous avons amené cette section à cet illustrateur. Même si Escher est mort il y a 20 ans, il nous a laissé son travail. Profitez-en !