Maurits Cornelis Escher (II)

1992/03/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

Partició periòdica de la superfície

No hi ha temes tan atractius com la partició periòdica de la superfície Escher. A aquest tema li va oferir un ampli tractat que deia: És la font de suggeriments més rica que he trobat i encara està molt lluny d'esgotar-se.

En 1922, sota la direcció del mestre de Mesquita, va realitzar en la seva fusta un dibuix amb vuit caps (quatre en veu) cobrint tota la superfície. Aquesta idea, no obstant això, no és imputable a Mesquita (figura 1).

Fins a 1926 semblava que aquest tema era una època de joventut. No obstant això, després de visitar l'Alhambra de Granada en 1926, Escher va intentar dotar a les seves imatges d'una estructura rítmica que no va aconseguir l'objectiu. En 1936 torna a visitar l'Alhambra amb Jetta. Amb ajuda de Jetta van copiar les seves imatges. Després de la lectura de llibres sobre adorns i alguns tractats matemàtics, en 1937 Escher va desenvolupar un sistema pràctic que escriuria en 1941 i 1942.

Mitjançant translacions, girs i moviments de reflexió podem aconseguir que una imatge s'ajusti a si mateixa. Algunes imatges només permeten la translació, unes altres la translació i gir, etc. En total són 17 les imatges que permeten aquests moviments sense modificar. Escher va aconseguir tots, encara que no tenia coneixements matemàtics per a això.

Les particions d'Escher es caracteritzaven perquè els temes triats per a repetir-ho sempre indicaven una cosa concreta. Referent a això va dir: Els àrabs van aconseguir un gran mestratge omplint la superfície amb imatges repetitives. Desgraciadament, l'islam els prohibia les imatges. Cap artista àrab es va atrevir a utilitzar imatges conegudes com a elements decoratius com a ocells, peixos, rèptils o persones. La limitació a les formes geomètriques em sembla inacceptable, ja que la possibilitat de conèixer imatges és la raó fonamental de l'interès permanent que tinc en aquesta matèria.

Escher no va treballar amb la partitura com a tema principal. En canvi, utilitzava la partició com a eina en metamorfosi i cicles. Encara que en algun treball només va treballar la metamorfosi (Metamorfosi I), en la majoria dels casos barrejava metamorfosis i cicles. En el llibre La partició periòdica de la superfície va aparèixer en 1958, Escher va explicar amb mestratge les diferents situacions d'una metamorfosi (Figura 2):

• En la fase 4, la imatge està dividida en paral·lelograms blancs i negres.
• En la fase 5 les línies divisores canvien de color i comencen a doblegar-se, corresponent a un plec exterior un altre interior.
• En les fases 6 i 7 se segueix el mateix procés mantenint la imatge obtinguda en la fase 7 fins a la seva finalització. No existeixen restes de paral·lelograms originals. No obstant això, és la mateixa superfície i tampoc s'han desplaçat els punts de contacte entre les imatges.
• En la fase 8, els detalls introduïts en figures negres converteixen als ocells en aletes, fent de les cares blanques la del cel.
• En la fase 9, no obstant això, els ocells blancs es troben sobre fons negre, cobrint el curat de la nit.
• En la fase 10, per què no es pot cobrir la superfície amb ocells blancs i negres?
• La fase 11 pot admetre dues interpretacions diferents. Representant l'ull i la boca en la cua dels ocells i convertint el cap en cua, les ales es converteixen automàticament en ales, convertint-se en peixos voladors.
• Finalment, en la fase 12 apareixen simultàniament dos tipus d'animals: ocells negres cap a la dreta i peixos blancs cap a l'esquerra.

La metamorfosi II, 1939-40, és la major imatge d'Escher. Les dimensions del dibuix són de 4 m de longitud i 20 cm d'alt. En 1967 es va ampliar sis vegades i Escher va allargar 3 m per a instal·lar-se en una Oficina de Correus. Aquest treball ens diu que la tècnica de la metamorfosi Escher no s'allargava massa. És sorprenent veure com es poden extreure les sargantanes dels quadrats per a convertir-les en hexàgons.

La imatge més admirada és el Dia i la nit (1939). El canvi entre el dia i la nit de dreta a esquerra és lent i la pujada del sòl al cel és lenta però segura.

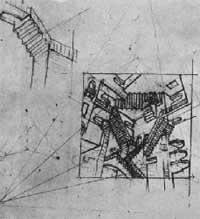
Entre els cicles es troba la litografia Cicle de 1938, en la qual la partició té tres punts de simetria diferents. En un d'ells es recullen els tres caps, en el segon els talons dels tres peus i el tercer és el punt de contacte dels tres genolls (figura 3). Un altre, Ángeles i dimonis (1941).

Figura .

En aquest cas, la partició periòdica té una simetria quàdruple. En tots els punts en els quals els extrems de les ales es toquen entre si podem fer un gir de 90è fins que la imatge s'ajusta a si mateixa (Figura 4). No obstant això, no tots els punts són iguals. Els punts A, P, Q, R i S són diferents dels punts B, C, D i E. També podem traçar la línia horitzontal i vertical des dels eixos de tots els àngels i dimonis, sent tots els eixos de simetria. D'altra banda, es poden traçar rectes que passen pels caps dels àngels i que formen un angle de 45° amb els eixos anteriors. Aquests no són eixos de simetria correctes, però si una vegada realitzada la reflexió sobre un eix es transforma en la seva adreça, la imatge no canviarà. Aquesta versió serà reutilitzada més tard per Escher per a elaborar limitis circulars i esferes.

Per a acabar direm que en 1942 Escher va fer un petit segell. En tots els costats del quadrat es poden veure tres enllaços. El segell es pot imprimir en quatre posicions. Amb aquest segell i el seu invers Escher va realitzar diferents dissenys (figura 5).

Perspectiva

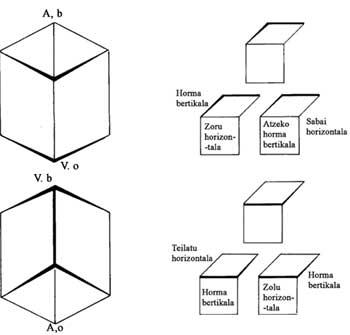
La perspectiva clàssica ens obliga a imaginar paral·lels al quadre. Aquestes línies, per tant, no tenen punts de fuita, o cosa que és el mateix, el seu punt de tall està en infinit. Per contra, la nostra experiència mira una torre des de baix, en la qual les línies verticals giren cap a un punt. Aquest punt és zenit. Si la mirada és descendent apareix el punt nadir. Aquest punt va ser explicat per Escher en el dibuix realitzat en la fusta de la torre de Babel de 1928 [1] i en el de Sant Pere de 1935, Roma [2]. Esche-r ho va utilitzar per primera vegada en 1946 com a punt de fuita en un "ex libris" (Sortirem).

Un altre món I, 1946 [3], i Un altre món II, 1947 [4], va intentar en imatges que Escher fos el zenit, el nadir i el mateix punt de fuita. El primer no li va agradar perquè el punt desapareixia en la foscor d'un túnel. En la segona, no obstant això, va aconseguir suggerir aquest triple punt mitjançant tres finestres dobles igualitàries. Una a l'interval que es veu per davant una altra es veu per sota i l'última per damunt, sent el punt de fuita del primer, el zenit del segon i el nadir de l'últim punt.

No obstant això, en la litografia de relativitat (1953) hi ha tres punts de fuita, formant un triangle equilàter de 2 metres fora del quadre (Figura 6). Aquí s'han reunit tres mons totalment diferents. Encara que no ho sembli, podria fer-se un model tridimensional de la imatge [5]. Els 16 éssers que apareixen es poden dividir en tres grups: els que estan dempeus per a nosaltres, els que tenen el cap a l'esquerra i els que tenen a la dreta. Dos de les tres escales situades en la part central poden ser utilitzades per les persones en peus. Poden fer-ho altres grups?. En l'escala superior hi ha dues persones de tot el món formant un angle recte. Pot succeir el mateix en altres ocasions?

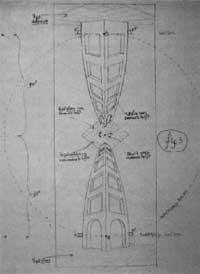
Per dalt i per baix en el dibuix les línies verticals són corbades i no rectes com indica la perspectiva tradicional (figura 7). Aquesta és la novetat dels Eschers en perspectiva. Les línies corbes s'ajusten millor a la nostra percepció de l'espai. Com se li va ocórrer a Escher substituir les línies rectes per corbades? Per a respondre a aquesta pregunta vegem la figura 8. Una persona observa les línies paral·leles que formen els fils entre dos pals. Els punts més pròxims són P i Q. Si mirem cap endavant, veurem que _{es dirigeixen cap al} punt V1 i mirant cap endarrere cap al punt V2. Mantenint la continuïtat de les línies, apareixen línies corbes.

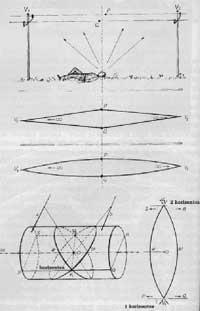
Però a quina llei geomètrica se segueixen aquestes línies?, quin tipus de corbes són?, són segments de cercles, hiperbolas o el·lipses?. L'esquema es mostra en la figura. Si l'ull està en el punt O, el que el veu el veu en la superfície d'un cilindre i els fils a i b en el cilindre es veuen com a' i b' el·lipse. Aquestes mitjanes _{es concentren en els} punts de fugida V1 i V2. Per a representar tot això en dues dimensions, tallant el cilindre per les línies PQ i RS i planejant la superfície superior, es converteixen en a' i b' sinusoides. Escher va arribar a aquest resultat de manera intuïtiva perquè no sabia el que eren sinusoides.

És un dels millors treballs des de dalt i a baix [6]. El punt central és el nadir de la part superior i el zenit de la inferior. Com hem dit, les línies verticals són corbades, però totes elles van cap al centre. Per a poder entendre bé aquesta imatge és necessari cobrir una primera meitat (superior o inferior) i després l'altra. Així, ens adonarem que des de dos punts de vista diferents (a dalt i a baix) veiem el mateix.

El paviment central apareix tres vegades: a dalt com a sostre, a baix com a fang i en el centre com a sostre i fang. Aquesta zona mitjana és el que ens sorprèn. Si passem de dalt a baix la línia central, es pot passar d'estar en el sòl a penjar i viceversa. La part superior no és un mirall de la inferior. Escher buscava en aquesta imatge dos efectes: el primer, corbar les línies verticals (i diverses horitzontals) i el segon, concentrar el nadir i el zenit en el mateix punt.

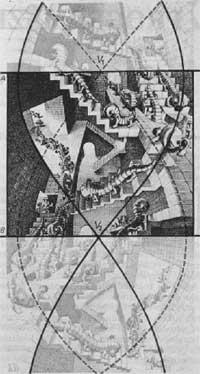
Va utilitzar la mateixa perspectiva en la litografia Caixa d'escales (1951) (Figura 9). S'han representat diverses línies de l'estructura que subjeu a la imatge. Això posa de manifest els dos punts de fuita des dels quals s'han dibuixat les línies horitzontals. Amb cada animaló d'artefacte es pot determinar si el punt de fuita és cenita, nadir o el punt més allunyat. Per exemple, per al gran animaló del mitjà V1 és el _punt més allunyat i V2 és el nadir.

D'aquí es dedueix que, per a cada animaló, les parets de la caixa tindran diferent significat (sostre, teix o mur).

El tram entre A i B té elements bàsics. Les parts superior i inferior de la imatge s'han construït mitjançant reflexos.

Algú podria pensar que la perspectiva cilíndrica que va utilitzar Escher podria estendre's a l'esfèrica. Escher no ho va fer, però per què no?