Maurits Cornelis Escher (II)

1992/03/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

Partición periódica de la superficie

No hay temas tan atractivos como la partición periódica de la superficie Escher. A este tema le ofreció un amplio tratado que decía: Es la fuente de sugerencias más rica que he encontrado y todavía está muy lejos de agotarse.

En 1922, bajo la dirección del maestro de Mesquita, realizó en su madera un dibujo con ocho cabezas (cuatro en voz) cubriendo toda la superficie. Esta idea, sin embargo, no es imputable a Mesquita (figura 1).

Hasta 1926 parecía que este tema era una época de juventud. Sin embargo, tras visitar la Alhambra de Granada en 1926, Escher intentó dotar a sus imágenes de una estructura rítmica que no logró el objetivo. En 1936 vuelve a visitar la Alhambra con Jetta. Con ayuda de Jetta copiaron sus imágenes. Tras la lectura de libros sobre adornos y algunos tratados matemáticos, en 1937 Escher desarrolló un sistema práctico que escribiría en 1941 y 1942.

Mediante traslaciones, giros y movimientos de reflexión podemos conseguir que una imagen se ajuste a sí misma. Algunas imágenes sólo permiten la traslación, otras la traslación y giro, etc. En total son 17 las imágenes que permiten estos movimientos sin modificar. Escher consiguió todos, aunque no tenía conocimientos matemáticos para ello.

Las particiones de Escher se caracterizaban por que los temas elegidos para repetirlo siempre indicaban algo concreto. A este respecto dijo: Los árabes consiguieron una gran maestría llenando la superficie con imágenes repetitivas. Desgraciadamente, el islam les prohibía las imágenes. Ningún artista árabe se atrevió a utilizar imágenes conocidas como elementos decorativos como pájaros, peces, reptiles o personas. La limitación a las formas geométricas me parece inaceptable, ya que la posibilidad de conocer imágenes es la razón fundamental del interés permanente que tengo en esta materia.

Escher no trabajó con la partitura como tema principal. En cambio, utilizaba la partición como herramienta en metamorfosis y ciclos. Aunque en algún trabajo sólo trabajó la metamorfosis (Metamorfosis I), en la mayoría de los casos mezclaba metamorfosis y ciclos. En el libro La partición periódica de la superficie apareció en 1958, Escher explicó con maestría las diferentes situaciones de una metamorfosis (Figura 2):

• En la fase 4, la imagen está dividida en paralelogramos blancos y negros.
• En la fase 5 las líneas divisoras cambian de color y comienzan a doblarse, correspondiendo a un pliego exterior otro interior.
• En las fases 6 y 7 se sigue el mismo proceso manteniendo la imagen obtenida en la fase 7 hasta su finalización. No existen restos de paralelogramos originales. Sin embargo, es la misma superficie y tampoco se han desplazado los puntos de contacto entre las imágenes.
• En la fase 8, los detalles introducidos en figuras negras convierten a las aves en aletas, haciendo de las caras blancas la del cielo.
• En la fase 9, sin embargo, las aves blancas se encuentran sobre fondo negro, cubriendo el curado de la noche.
• En la fase 10, ¿por qué no se puede cubrir la superficie con aves blancas y negras?
• La fase 11 puede admitir dos interpretaciones diferentes. Representando el ojo y la boca en la cola de las aves y convirtiendo la cabeza en cola, las alas se convierten automáticamente en alas, convirtiéndose en peces voladores.
• Por último, en la fase 12 aparecen simultáneamente dos tipos de animales: aves negras hacia la derecha y peces blancos hacia la izquierda.

La metamorfosis II, 1939-40, es la mayor imagen de Escher. Las dimensiones del dibujo son de 4 m de longitud y 20 cm de alto. En 1967 se amplió seis veces y Escher alargó 3 m para instalarse en una Oficina de Correos. Este trabajo nos dice que la técnica de la metamorfosis Escher no se alargaba demasiado. Es sorprendente ver cómo se pueden extraer las lagartijas de los cuadrados para convertirlas en hexágonos.

La imagen más admirada es el Día y la noche (1939). El cambio entre el día y la noche de derecha a izquierda es lento y la subida del suelo al cielo es lenta pero segura.

Entre los ciclos se encuentra la litografía Ciclo de 1938, en la que la partición tiene tres puntos de simetría diferentes. En uno de ellos se recogen las tres cabezas, en el segundo los talones de los tres pies y el tercero es el punto de contacto de las tres rodillas (figura 3). Otro, Ángeles y demonios (1941).

Figura .

En este caso, la partición periódica tiene una simetría cuádruple. En todos los puntos en los que los extremos de las alas se tocan entre sí podemos hacer un giro de 90º hasta que la imagen se ajusta a sí misma (Figura 4). Sin embargo, no todos los puntos son iguales. Los puntos A, P, Q, R y S son diferentes de los puntos B, C, D y E. También podemos trazar la línea horizontal y vertical desde los ejes de todos los ángeles y demonios, siendo todos los ejes de simetría. Por otra parte, se pueden trazar rectas que pasan por las cabezas de los ángeles y que forman un ángulo de 45º con los ejes anteriores. Estos no son ejes de simetría correctos, pero si una vez realizada la reflexión sobre un eje se transforma en su dirección, la imagen no cambiará. Esta versión será reutilizada más tarde por Escher para elaborar limites circulares y esferas.

Para terminar diremos que en 1942 Escher hizo un pequeño sello. En todos los lados del cuadrado se pueden ver tres enlaces. El sello se puede imprimir en cuatro posiciones. Con este sello y su inverso Escher realizó diferentes diseños (figura 5).

Perspectiva

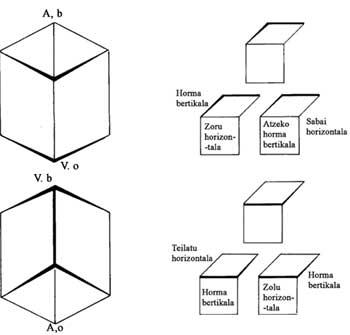
La perspectiva clásica nos obliga a imaginar paralelos al cuadro. Estas líneas, por tanto, no tienen puntos de escape, o lo que es lo mismo, su punto de corte está en infinito. Por el contrario, nuestra experiencia mira una torre desde abajo, en la que las líneas verticales giran hacia un punto. Este punto es cenit. Si la mirada es descendente aparece el punto nadir. Este punto fue explicado por Escher en el dibujo realizado en la madera de la torre de Babel de 1928 [1] y en el de San Pedro de 1935, Roma [2]. Esche-r lo utilizó por primera vez en 1946 como punto de escape en un "ex libris" (Saldremos).

Otro mundo I, 1946 [3], y Otro mundo II, 1947 [4], intentó en imágenes que Escher fuese el cenit, el nadir y el mismo punto de escape. El primero no le gustó porque el punto desaparecía en la oscuridad de un túnel. En la segunda, sin embargo, consiguió sugerir este triple punto mediante tres ventanas dobles igualitarias. Una al intervalo que se ve por delante otra se ve por debajo y la última por encima, siendo el punto de escape del primero, el cenit del segundo y el nadir del último punto.

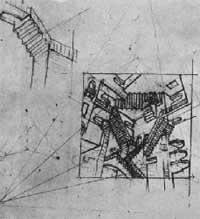
Sin embargo, en la litografía de relatividad (1953) hay tres puntos de escape, formando un triángulo equilátero de 2 metros fuera del cuadro (Figura 6). Aquí se han reunido tres mundos totalmente diferentes. Aunque no lo parezca, podría hacerse un modelo tridimensional de la imagen [5]. Los 16 seres que aparecen se pueden dividir en tres grupos: los que están de pie para nosotros, los que tienen la cabeza a la izquierda y los que tienen a la derecha. Dos de las tres escaleras situadas en la parte central pueden ser utilizadas por las personas en pie. ¿Pueden hacerlo otros grupos?. En la escalera superior hay dos personas de todo el mundo formando un ángulo recto. ¿Puede suceder lo mismo en otras ocasiones?

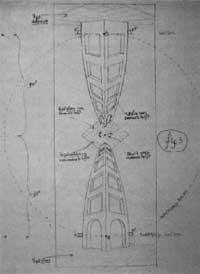
Por arriba y por abajo en el dibujo las líneas verticales son curvadas y no rectas como indica la perspectiva tradicional (figura 7). Esta es la novedad de los Eschers en perspectiva. Las líneas curvas se ajustan mejor a nuestra percepción del espacio. ¿Cómo se le ocurrió a Escher sustituir las líneas rectas por curvadas? Para responder a esta pregunta veamos la figura 8. Una persona observa las líneas paralelas que forman los hilos entre dos postes. Los puntos más cercanos son P y Q. Si miramos hacia delante, veremos que _{se dirigen hacia el} punto V1 y mirando hacia atrás hacia el punto V2. Manteniendo la continuidad de las líneas, aparecen líneas curvas.

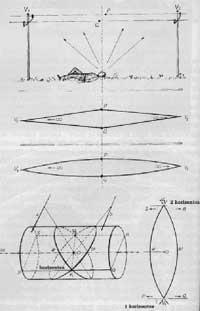
Pero ¿a qué ley geométrica se siguen estas líneas?, ¿qué tipo de curvas son?, ¿son segmentos de círculos, hiperbolas o elipses?. El esquema se muestra en la figura. Si el ojo está en el punto O, el que lo ve lo ve en la superficie de un cilindro y los hilos a y b en el cilindro se ven como a' y b' elipse. Estas medias _{se concentran en los} puntos de fuga V1 y V2. Para representar todo esto en dos dimensiones, cortando el cilindro por las líneas PQ y RS y planeando la superficie superior, se convierten en a' y b' sinusoides. Escher llegó a este resultado de forma intuitiva porque no sabía lo que eran sinusoides.

Es uno de los mejores trabajos desde arriba y abajo [6]. El punto central es el nadir de la parte superior y el cenit de la inferior. Como hemos dicho, las líneas verticales son curvadas, pero todas ellas van hacia el centro. Para poder entender bien esta imagen es necesario cubrir una primera mitad (superior o inferior) y luego la otra. Así, nos daremos cuenta de que desde dos puntos de vista diferentes (arriba y abajo) vemos lo mismo.

El pavimento central aparece tres veces: arriba como techo, abajo como fango y en el centro como techo y fango. Esta zona media es lo que nos sorprende. Si pasamos de arriba a abajo la línea central, se puede pasar de estar en el suelo a colgar y viceversa. La parte superior no es un espejo de la inferior. Escher buscaba en esta imagen dos efectos: el primero, curvar las líneas verticales (y varias horizontales) y el segundo, concentrar el nadir y el zenit en el mismo punto.

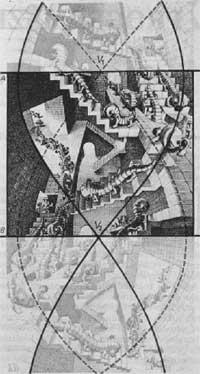
Utilizó la misma perspectiva en la litografía Caja de escaleras (1951) (Figura 9). Se han representado varias líneas de la estructura que subyace a la imagen. Esto pone de manifiesto los dos puntos de escape desde los que se han dibujado las líneas horizontales. Con cada animalito de artilugio se puede determinar si el punto de escape es cenita, nadir o el punto más alejado. Por ejemplo, para el gran animalito del medio V1 es el _punto más alejado y V2 es el nadir.

De aquí se deduce que, para cada animalito, las paredes de la caja tendrán diferente significado (techo, tejo o muro).

El tramo entre A y B tiene elementos básicos. Las partes superior e inferior de la imagen se han construido mediante reflejos.

Alguien podría pensar que la perspectiva cilíndrica que utilizó Escher podría extenderse a la esférica. Escher no lo hizo, pero ¿por qué no?