Maurits Cornelis Escher (II)

1992/03/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

Partition périodique de la surface

Il n'y a pas de sujets aussi attrayants que la partition périodique de la surface Escher. À ce sujet, il a offert un vaste traité qui disait: C'est la source de suggestions la plus riche que j'ai trouvé et il est encore loin de s'épuiser.

En 1922, sous la direction du maître de Mesquita, il réalise dans son bois un dessin à huit têtes (quatre à voix) couvrant toute la surface. Cette idée, cependant, n'est pas imputable à Mesquita (Figure 1).

Jusqu'en 1926, il semblait que ce thème était une époque de jeunesse. Cependant, après avoir visité l'Alhambra de Grenade en 1926, Escher a essayé de doter ses images d'une structure rythmique qui n'a pas atteint l'objectif. En 1936, il revisite l'Alhambra avec Jetta. Avec l'aide de Jetta, ils ont copié leurs images. Après la lecture de livres sur les ornements et certains traités mathématiques, en 1937 Escher a développé un système pratique qu'il a écrit en 1941 et 1942.

Grâce à des mouvements de réflexion, des virages et des mouvements, nous pouvons obtenir une image qui s'adapte. Certaines images ne permettent que la traduction, d'autres la traduction et la rotation, etc. Au total, 17 images permettent ces mouvements sans modifier. Escher a obtenu tous, bien qu'il n'avait aucune connaissance mathématique pour cela.

Les partitions d'Escher étaient caractérisées par le fait que les thèmes choisis pour le répéter indiquaient toujours quelque chose de concret. À cet égard, il a dit: Les Arabes ont obtenu une grande maîtrise remplissant la surface avec des images répétitives. Malheureusement, l'islam leur interdisait les images. Aucun artiste arabe n'a osé utiliser des images connues comme des éléments décoratifs tels que des oiseaux, des poissons, des reptiles ou des personnes. La limitation des formes géométriques me semble inacceptable, puisque la possibilité de connaître des images est la raison fondamentale de l'intérêt permanent que j'ai en cette matière.

Escher n'a pas travaillé avec la partition comme thème principal. Au lieu de cela, j'ai utilisé la partition comme outil dans la métamorphose et les cycles. Bien que dans certains travaux seulement travaillé la métamorphose (Métamorphose I), dans la plupart des cas mélangé métamorphoses et cycles. Dans le livre La partition périodique de la surface est apparu en 1958, Escher a expliqué avec maîtrise les différentes situations d'une métamorphose (Figure 2):

• Dans la phase 4, l'image est divisée en parallélogrammes blancs et noirs.
• Dans la phase 5 les lignes divisantes changent de couleur et commencent à se plier, correspondant à un pliage extérieur un autre intérieur.
• Dans les phases 6 et 7 on suit le même processus en maintenant l'image obtenue dans la phase 7 jusqu'à son achèvement. Il n'y a pas de traces de parallélogrammes originaux. Cependant, c'est la même surface et les points de contact entre les images n'ont pas été déplacés.
• Dans la phase 8, les détails introduits en figures noires transforment les oiseaux en nageoires, faisant des faces blanches celle du ciel.
• Dans la phase 9, cependant, les oiseaux blancs se trouvent sur fond noir, couvrant le durcissement de la nuit.
• Dans la phase 10, pourquoi ne peut-on pas couvrir la surface avec des oiseaux blancs et noirs?
• La phase 11 peut admettre deux interprétations différentes. Représentant l'œil et la bouche dans la queue des oiseaux et transformer la tête en queue, les ailes deviennent automatiquement des ailes, devenant des poissons volants.
• Enfin, dans la phase 12, deux types d'animaux apparaissent simultanément : oiseaux noirs à droite et poissons blancs à gauche.

La métamorphose II, 1939-40, est la plus grande image d'Escher. Les dimensions du dessin sont de 4 m de longueur et 20 cm de hauteur. En 1967, il agrandit six fois et Escher allonge 3 m pour s'installer dans un bureau de poste. Ce travail nous dit que la technique de la métamorphose Escher ne s'allongeait pas trop. Il est surprenant de voir comment on peut extraire les lézards des carrés pour les convertir en hexagones.

L'image la plus admirée est le jour et la nuit (1939). Le changement entre le jour et la nuit de droite à gauche est lent et la montée du sol au ciel est lente mais sûre.

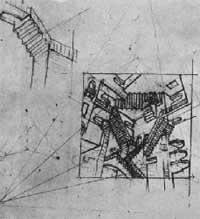
Parmi les cycles se trouve la lithographie Cycle de 1938, dans laquelle la partition a trois points de symétrie différents. Dans l'un d'eux sont recueillies les trois têtes, dans le second les talons des trois pieds et le troisième est le point de contact des trois genoux (Figure 3). Un autre, Anges et démons (1941).

Figure .

Dans ce cas, la partition périodique a une symétrie quadruple. À tous les points où les extrémités des ailes se touchent, nous pouvons faire un tour de 90° jusqu'à ce que l'image s'ajuste (figure 4). Cependant, tous les points ne sont pas égaux. Les points A, P, Q, R et S sont différents des points B, C, D et E. Nous pouvons aussi tracer la ligne horizontale et verticale depuis les axes de tous les anges et démons, étant tous les axes de symétrie. D'autre part, on peut tracer droites qui passent par les têtes des anges et qui forment un angle de 45° avec les axes précédents. Ce ne sont pas des axes de symétrie corrects, mais si une fois réalisée la réflexion sur un axe se transforme en direction, l'image ne changera pas. Cette version sera réutilisée plus tard par Escher pour élaborer des limites circulaires et sphères.

Pour finir, on dira qu'en 1942 Escher fit un petit sceau. Sur tous les côtés du carré, vous pouvez voir trois liens. Le timbre peut être imprimé en quatre positions. Avec ce sceau et son inverse Escher a réalisé différents modèles (figure 5).

Perspective

La perspective classique nous oblige à imaginer des parallèles au tableau. Ces lignes n'ont donc pas de points d'échappement, ou ce qui est la même chose, leur point de coupe est infinie. Au contraire, notre expérience regarde une tour d'en bas, dans laquelle les lignes verticales tournent vers un point. Ce point est zénith. Si le regard est descendant, le point nadir apparaît. Ce point fut expliqué par Escher dans le dessin réalisé sur le bois de la tour de Babel de 1928 [1] et celui de Saint-Pierre de 1935, Rome [2]. Esche-r l'utilisa pour la première fois en 1946 comme point d'échappement dans un "ex libris" (Nous sortirons).

Un autre monde I, 1946 [3], et Un autre monde II, 1947 [4], tenta en images qu'Escher fût le zénith, le nadir et le même point d'échappement. Le premier n'a pas aimé parce que le point disparaissait dans l'obscurité d'un tunnel. Dans la seconde, cependant, il a réussi à suggérer ce triple point par trois doubles fenêtres égalitaires. Une à l'intervalle que l'on voit en avant une autre est vu en dessous et la dernière au-dessus, étant le point d'échappement du premier, le zénith du second et le nadir du dernier point.

Cependant, dans la lithographie de relativité (1953) il y a trois points d'échappement, formant un triangle équilatéral de 2 mètres en dehors du tableau (Figure 6). Ici se sont réunis trois mondes totalement différents. Même si cela n'est pas le cas, un modèle tridimensionnel de l'image pourrait être fait [5]. Les 16 êtres qui apparaissent peuvent être divisés en trois groupes: ceux qui se tiennent pour nous, ceux qui ont la tête à gauche et ceux qui ont à droite. Deux des trois escaliers situés dans la partie centrale peuvent être utilisés par les personnes debout. D'autres groupes peuvent-ils le faire ? Sur l'escalier supérieur, deux personnes du monde entier forment un angle droit. La même chose peut-elle arriver à d'autres occasions ?

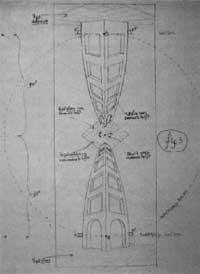
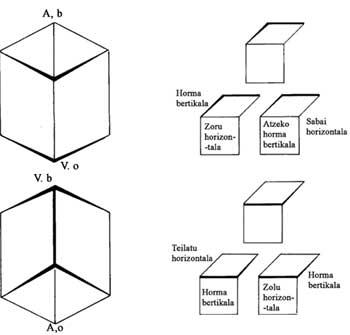
En haut et en bas sur le dessin les lignes verticales sont incurvées et non droites comme l'indique la perspective traditionnelle (figure 7). Telle est la nouveauté des Eschers en perspective. Les lignes courbes sont mieux adaptées à notre perception de l'espace. Comment Escher est-il arrivé de remplacer les lignes droites par des courbes ? Pour répondre à cette question, voyons la figure 8. Une personne observe les lignes parallèles formant les fils entre deux poteaux. Les points les plus proches sont P et Q. Si nous regardons en avant, nous verrons _{qu'ils se dirigent vers le} point V1 et regardent en arrière vers le point V2. En maintenant la continuité des lignes, des lignes courbes apparaissent.

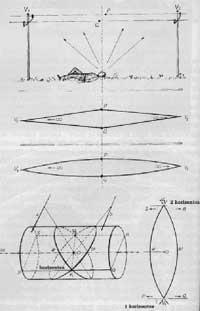
Mais à quelle loi géométrique ces lignes sont-elles suivies ? quels types de courbes sont?, Sont des segments de cercles, hyperbilles ou ellipses? Le schéma est affiché dans la figure. Si l'oeil est au point O, celui qui le voit le voit sur la surface d'un cylindre et les fils a et b dans le cylindre sont vus comme a' et b'elipse. Ces collants _{sont concentrés sur les} points de fuite V1 et V2. Pour représenter tout cela en deux dimensions, en coupant le cylindre par les lignes PQ et RS et en projetant la surface supérieure, deviennent a' et b' sinusoïdes. Escher est venu à ce résultat de manière intuitive parce qu'il ne savait pas ce qu'ils étaient sinusoïdes.

C'est l'un des meilleurs travaux de haut en bas [6]. Le point central est le nadir du haut et le zénith du bas. Comme nous l'avons dit, les lignes verticales sont courbées, mais toutes vont vers le centre. Pour bien comprendre cette image, il faut couvrir une première moitié (supérieure ou inférieure) puis l'autre. Ainsi, nous réaliserons que de deux points de vue différents (haut et bas) nous voyons la même chose.

Le plancher central apparaît trois fois : haut comme plafond, bas comme boue et au centre comme toit et boue. Cette zone moyenne est ce qui nous surprend. Si nous passons de haut en bas de la ligne centrale, vous pouvez passer d'être sur le sol à accrocher et vice versa. La partie supérieure n'est pas un miroir de la partie inférieure. Escher cherchait dans cette image deux effets : le premier, cintrer les lignes verticales (et plusieurs horizontales) et le second, concentrer le nadir et le zenit au même point.

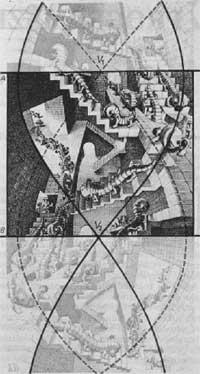
Il a utilisé la même perspective dans la lithographie Caisse d'escalier (1951) (Figure 9). Plusieurs lignes de la structure sous-jacente à l'image ont été représentées. Cela montre les deux points d'échappement depuis lesquels les lignes horizontales ont été dessinées. Avec chaque petit animal, vous pouvez déterminer si le point d'échappement est zénith, nadir ou le point le plus éloigné. Par exemple, pour le grand petit animal du milieu V1 est le _point le plus éloigné et V2 est le nadir.

Il s'ensuit que, pour chaque petit animal, les murs de la boîte auront une signification différente (toit, tuile ou mur).

Le tronçon entre A et B a des éléments de base. Les parties supérieure et inférieure de l'image ont été construites par des reflets.

Quelqu'un pourrait penser que la perspective cylindrique qui a utilisé Escher pourrait s'étendre à la sphérique. Escher ne l'a pas fait, mais pourquoi pas?