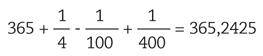Merece a pena que o ano 3200 sexa bianual?

2014/01/01 Alberdi Celaya, Elisabete - Matematikan lizentziatua eta doktoregaia Iturria: Elhuyar aldizkaria

• Historia
• Matematika

Contamos de diferentes maneiras o número de días que falta paira chegar a un día concreto. Fai 13.000 anos, os humanos de Cro-Magnon, paira contar os días que había entre a primeira xeada de inverno e a primavera, contaban lúas cheas; os presos contaron con raias o número de días que faltaban paira deixar o cárcere e ser libres; e contan o tempo que teñen que durmir os nenos paira chegar a Olentzero. Baseado nas etapas da Lúa, con raias ou o número de duelos que hai que facer como unidade, son exemplos dun calendario que todos levamos colgado na parede, encima da mesa ou gardado no moedeiro.

Primeiro calendario: Baseado nas etapas da Lúa

Ao ser humano vénlle desde hai tempo a obsesión por medir o tempo. En tempos nos que somos capaces de medir nanosegundos (10 -9 segundos) e femtosegundos (10 -15 segundos), quizais nos resulte estraño o percorrido do home en busca dun calendario concreto, pero así foi: o calendario concreto e útil foi durante moito tempo uno dos retos máis importantes do ser humano.

Aínda que non todos os calendarios de tempos antigos funcionan da mesma maneira, si que teñen varias características comúns. Por exemplo, a maioría dos calendarios son cíclicos, é dicir, una vez cumprido un período, repítense. A maioría delas exprésanse de forma circular, xa que nas culturas de outrora representaban ao firmamento como disco, círculo ou esfera. Esta esfera dividíase en meses lunares ou de sol e o ceo distribuíase en 360 días ao ano ou 360 graos.

Os astrónomos da Idade de Pedra observaron os períodos da Lúa, xa que se deron conta de que podían contar as noites entre os momentos da Lúa chea, semillena e totalmente escura, e que se repetían. Así, algúns antropólogos consideran que o calendario dos primeiros que utilizou o ser humano é o formado por varias muescas realizadas nun óso de aguia, formadas por unha impresión regular de diferentes agrupacións de símbolos similares.

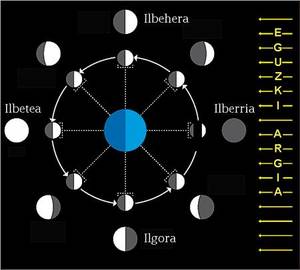
A lúa necesita uns 29 días e medio (29,5306 días) paira pasar da lúa á lúa crecente, da lúa crecente á lúa chea, da lúa en cuarto menguante e da lúa en cuarto menguante. Doce ciclos completos da Lúa cobren aproximadamente as catro estacións do ano, que conformaban o que as sociedades de entón xa coñecían como un ano. Gregos, xudeus, chineses... utilizaron o ano lunar, composto por 12 meses de 29 días e medio, cun total de 354 días.

Con todo, os que dispuñan dun calendario baseado nos períodos lunares non tardaron moito en darse conta de que o seu ano tiña algún erro, xa que no seu calendario son 8 anos suficientes para que o comezo da primavera producísese a principios do verán do seu calendario, e así, en 16 anos, o comezo do verán coincidía co comezo do inverno. Paira corrixir o erro detectado no ano lunar, os gregos engadían 90 días no seu calendario cada 8 anos, os xudeus engadían un mes lunar cada 3 anos e os matemáticos chineses dicían que cada 19 anos había que engadir 7 meses lunares.

Da lúa ao ano solar

Sumer a.C. XXI. No século XX estabamos nun ano de 360 días, consecuencia do redondeo do mes lunar a 30 días. O sistema sumerio baseábase nos números 6 e 60. A multiplicación de ambos os números dá 360, e ese número segue sendo o que utilizamos paira distribuír o cimacio ou calquera plano circular. Os Babilonios herdaron o sistema de numeración dos sumerios e repartiron o día 24 horas. Aínda que non se sabe o porqué, parece que é un número relacionado co zodiaco e que lle levou as súas crenzas astrológicas.

O ano solar é a duración do movemento de translación da Terra ao redor do Sol, que comprende 365,242190 días. Fai uns 6.000 anos, o exipcio corrixiu o erro do ano lunar e tomou o ano solar a primeira civilización. O seu calendario tiña 12 meses de 30 días e 5 días adicionais. Estes cinco días adicionais convertéronse en días de deuses Osiris, Isis, Horus, Neftis e Set. Aínda que é un misterio como os exipcios fixeron tan boa aproximación ao ano solar, a explicación máis crible atopámola no río Nilo: Desde finais de xuño até finais de outubro producíanse inundacións no río Nilo, que deixaba un bo chan paira a colleita desde outubro a febreiro, polo que desde febreiro até finais de xuño recollíase una abundante colleita nos terreos lindeiros ao río. Por tanto, os habitantes da zona só debían contar os días entre unha inundación e a seguinte paira calcular a duración do ano solar. Os astrónomos exipcios tamén se deron conta de que o ano solar era un cuarto de día máis longo do calendario que eles mesmos tiñan, e que o ano C. No ano 238 a duración do ano solar estableceuse en 365 1/4 días.

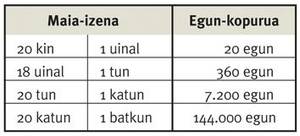
Pero os exipcios non foron os únicos que utilizaron o calendario de 365 días. Os mayas utilizaron 3 sistemas de calendario, nun dos cales a duración do ano era de 365 días. Uno dos calendarios utilizados polos mayas é o chamado calendario civil ( haab ), o segundo é o chamado calendario sacro ( tzolkin ) e o terceiro é o chamado relato longo. O calendario Haab ten 18 meses de 20 días e un mes de 5 días, cun total de 365 días. Parece que os mayas tamén sabían que a duración do ano era de 365 1/4 días, aínda que no seu calendario non tiñan en conta o cuarto de día. O calendario de Tzolkin ten 260 días e o sistema de conta longa baséase en unidades de 360 días, utilizando a unidade tun e o número 20. Paira eles o batkun é un intervalo de tempo de 144.000 días, e multiplicando o batkun por 13 conseguen o que se denomina ciclo longo, cunha duración aproximada de 5.130 anos. Eles crían que, tras un longo ciclo, até entón desaparecía, dando paso a un novo mundo. O 21 de decembro de 2012 finaliza o seu último ciclo, a. C. Iniciado cara ao 3114. Aínda que non se sabe con certeza, os mayas deron a lonxitude do seu ano baseándose en observacións astronómicas.

O noso calendario: calendario gregoriano

Na actualidade, o calendario que utilizamos na maior parte do mundo é gregoriano, o XVI. Implantado no século XVIII polo Papa Gregorio XIII. O seu obxectivo era que a duración do ano deste calendario fose o máis parecida posible á do ano solar. O calendario gregoriano é o calendario solar: Composto por 365 días e 12 meses, que inclúe un día adicional nos bienios. Un ano é biaño cando é múltiplo de catro números. A excepción son os anos que son múltiplos de 100, que son só bisaños cando son múltiplos de 400. Por exemplo, 1700., Os anos 1800 e 1900 non son anos bisiestos, pero o 2000 é biaño. Calendarios gregorianos Xullo César. Substituíu ao calendario juliano establecido no ano 45. A principal diferenza entre eles é que no calendario juliano todos os anos eran múltiplos do número 4. O ano do calendario juliano tiña una media de 365,25 días. No calendario gregoriano, pola contra, ao non ser 3 anos de 4 a 3 anos múltiplos de 100, nun ciclo de 400 anos, no canto de 100 anos, hai 97 anos de visados, o que supón 400 x 365 + 97 = 146.097 días. Isto dános un ano de 146.097/400 = 365,2425 días de duración media. Por tanto, o calendario gregoriano achégase mellor ao ano solar que o calendario juliano.

Cara aos 1.600 anos que levaba o calendario juliano tiña un erro acumulado duns 10 días con respecto ao calendario gregoriano (e tamén con respecto ao ano solar), é dicir, 10 días despois. Paira emendar este erro, cando se estableceu o calendario gregoriano, ao 4 de outubro de 1582 do calendario juliano, seguiu o 15 de outubro de 1582 do calendario gregoriano. Os países católicos, como España, Portugal e Italia, aprobaron inmediatamente o calendario gregoriano.

Con todo, o calendario gregoriano tampouco dá una duración exacta do ano solar, cunha diferenza de 3,1·10 -4 días. É dicir, o calendario gregoriano introduce un día adicional ao ano solar cada 3.225 anos aproximadamente. Podemos pensar noutro calendario que reduza o erro deste calendario?

A duración do calendario gregoriano pode calcularse da seguinte maneira:

Dado que o ano do calendario gregoriano é máis longo que o ano solar, por exemplo, pódense quitar algúns anos de visado para que se achegue máis á duración do ano solar. Por exemplo, se restamos a condición de bisaño aos múltiplos de 3.200, a duración do ano sería:

É dicir, se o bisaño é múltiplo de 4, pero só é múltiplo de 100 si é múltiplo de 400, pero non é múltiplo de 3.200, temos un calendario que se achega mellor ao ano solar. Non é raro que apareza o número 3.200, xa que, como se dixo anteriormente, o calendario gregoriano inclúe un día adicional cada 3.225 anos.

Paira terminar...

No calendario gregoriano, este ano é 2014; no calendario coreano, o 4347a; no calendario maya, o 2º ano do novo período; no chinés, o ano do cabalo... O obxectivo de todos é achegarnos o máximo posible ao ano solar. Se o ano solar fose un número normal, todo sería máis fácil e non necesitariamos visados. A pesar de que cada 3.200 anos mellórase a precisión do calendario gregoriano eliminando un día, non é necesario facelo, xa que nese período non hai nada que meter un erro dun día, e nese período modifícanse os ciclos do Sol, a Terra, etc.

Non seremos os que imos modificar o calendario gregoriano que non sufriu cambios desde que nós establecémolo, deixaremos de traballar os cambios de ciclo. Quen sabe, quizá a duración do ano solar pase a ser de 365 días concretos, o que facilitará as tarefas de elaboración do calendario.

Bibliografía