Mezclado III

1991/12/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

Las vacaciones de Navidad nos permiten disfrutar de este pequeño descanso que merecemos. Sin embargo, nuestra costumbre de trabajar no nos deja la cabeza tranquila y muchas veces estamos haciendo algún trabajo para casa. Para que no te pase eso, te ofrecemos 25 cuestionarios para que te entretengas en estos días de mucho prestigio.

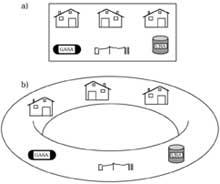
1. A continuación se muestran tres casas y depósitos de agua, luz y gas situados en el plano (a). Los barrios quieren conectar sus casas con las guardas, pero sin cruzar las tuberías. ¿Les ayudaría?

En la inferior (b), las casas y las guardas se encuentran en suelo de rosquilla. Los barrios tienen el mismo problema. ¿Van a conseguir la solución?

2. Tienes que formar una imagen de ocho poxpolos con cuatro triángulos y dos cuadrados.

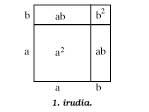
3. Hay que realizar cuatro cortes rectos a un cuadrado. Con las piezas obtenidas tendrás que completar cinco cuadrados iguales.

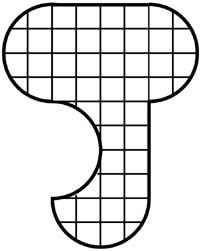
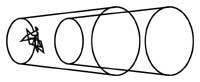
4º Recorta la imagen lateral en dos partes iguales.

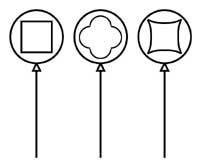
5. Si dibujas un cuadrado en el globo vaciado, ¿qué aspecto tendrá después de inflar el globo?

6º ¿Cómo sacarías el papel sin tocar los bosques?

7. Un hombre llega a su casa por la noche. Pronto se da cuenta de algo y se suicida cogiendo la pistola. Pero si hubiera visto serrín en el suelo de su casa no se habría matado. ¿Cuál es la causa de este extraño comportamiento?

8º. Supongamos que alguien ha multiplicado todos los primeros números (por supuesto los que se conocen). Si el producto es L:

• ¿Cuál es la última cifra de L?
• la última cifra es impar o par?

9. Tres hermanos miente tres días a la semana, y en otros casos dicen la verdad. El jefe miente los lunes, martes y miércoles. Los del centro los miércoles, jueves y viernes. Los más jóvenes los viernes, sábados y domingos. Una vez en Loyola, reunidos los tres hermanos, dijeron:

Nerea: hoy viernes es Josune: ayer jueves era Gorka: Josune es la principal

¿Qué día de la semana se produjo esta entrevista? ¿Cómo se llaman los mayores, los medios y los más jóvenes?

10. Igual dejando el número de poxpolos que hay a ambos lados del símbolo, ¿cómo hacer la igualdad?

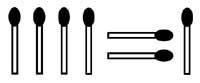
11. A un lado de una tarjeta se puede leer la frase “en esta tarjeta hay dos afirmaciones”. En el otro lado, la frase “lo que se dice detrás no es cierto”. ¿Cuál es la mentira?

12. En dos bosques tenemos el agua y el vino, la misma cantidad. Del agua se toman cinco gotas y se añaden al vino. Tras agitar este bosque se toman cinco gotas que se dejan en el bosque del agua. ¿Hay más agua en el vino que vino? ¿O al revés?

13. En total, siete sultanes tienen 2.879 mujeres. No hay igual cantidad. Si dividimos el número de mujeres de cualquiera de las filas por el número de otras tantas, siempre obtendremos el número entero.

¡Di así Allah!, cuántas mujeres hay en cada partido.

14. Subí a un cerezo que tenía cereza.

No comí cerezas, pero la dejé sin cerezas.

¿Cuántas cerezas había en el árbol?

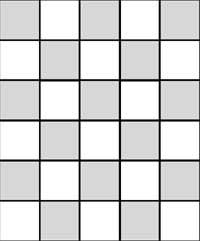
15. Con las siguientes piezas se debe completar el cuadro de ajedrez. Las piezas se pueden girar en el plano, pero no en el espacio.

16. Un problema de ajedrez consiste en colocar en una tabla de las cuadrículas 5x6 al rey, la dama, dos torres, dos alfiles (en diferentes colores) y dos caballos sin agredir entre sí.

Se puede introducir una dificultad. Se colocará un peón en las mismas condiciones, pero no en la primera y última fila.

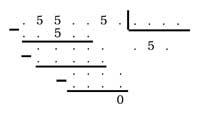
17. He aquí una división en la que sólo se ven 5 y 0. Debes sustituir los puntos por números para conocer la división.

18. Coloca los números del 1 al 12 en círculos blancos para que las sumas de los seis números de los aros sean iguales.

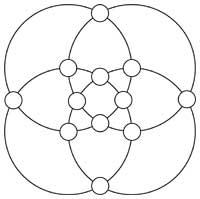
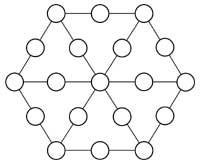
19. Ahora similar, pero esta vez con números del 1 al 19, para que la suma en las líneas de tres círculos (incluidos los radios) sea 22. Una vez conseguido esto, vuelve a colocar los números para que la suma sea 23.

20. Hay tres cartas boca abajo. Sabemos que a la derecha de un 1 hay 2 o 2; a la izquierda de un 2 hay 2 o 2; a la izquierda de una copa hay una o dos espadas y, por último, a la derecha de una espada hay una o dos espadas. ¿Cuáles son las tres cartas?

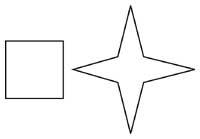
21. Con cuatro secciones adecuadas al cuadrado contiguo puedes conseguir una estrella de cuatro vértices.

22. En la imagen se puede ver un rectángulo formado por baldosas en forma de L. Este rectángulo tiene una ranura que divide en dos rectángulos. El menor rectángulo que se puede realizar sin ranuras con baldosa en forma de L es la mitad de la figura. Pero, ¿cuál es el siguiente?

23. Otra división. En ella los números impares están representados por cuadrados y los pares por círculos. Es una división exacta.

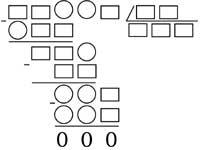
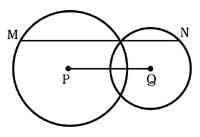
24. Los centros de las circunferencias de la figura se encuentran en los puntos P y Q, siendo la longitud del segmento PQ de 3 cm. ¿Cuál es la longitud del segmento MN que pasa por un punto de corte y paralelo al PQ?

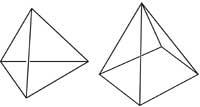
25. He aquí dos pirámides. En ambos extremos las longitudes son iguales. ¿Cuáles son los volúmenes de las pirámides? (sin cálculo).

Si tienes un hueco entre juernas para intentar responder a estos interrogantes, muchas gracias. Seguramente lo has conseguido y no tendrás que pedir respuestas. Sin embargo, si no lo has intentado (todavía estás a tiempo) o si, a pesar de haberlo intentado, no has encontrado todas las respuestas, te gustaría que lo hicieras para comprobarlas o para conocer las que no has encontrado. En tal caso, indíquenos y le indicamos que recibirá la respuesta adecuada.