Barrejat IV

1992/07/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

Sembla que quan ens acostem a unes vacances la publicació d'una nova col·lecció de desordres s'està convertint en un costum. Aquesta és la nostra intenció. Al llarg de l'any abordarem temes més seriosos (com fins ara) i en el número de juliol-agost, amb l'objectiu de relaxar la ment o llançar una col·lecció com aquesta. Mentre no rebem cap opinió en contra, ho farem així. Respecte al gra de desembre, no obstant això, estem en el meu poder. En aquesta època també tenim dies lliures. No obstant això, tenim el dubte que treure dues col·leccions d'aquest tipus en el mateix any no és massa. Què opines?

D'altra banda, tots sabem coses com les que apareixen aquí, jocs, raguis… Volem proposar-nos que ens enviïs els teus coneixements i el teu nom i et prometem que els publicarem completament.

Les respostes a les preguntes que es plantegen en el següent número, és a dir, en el número 63. I per a acabar, aquest apartat vol ser un lloc d'intercanvi de lectors, però per a això necessitem la teva col·laboració. Anima't!.

1. El de Zirano Bergerac ho va plantejar en el seu viatge a la lluna. Sabem que quan tirem dels extrems d'una corda es trenca del punt més feble. Suposem que tenim una corda amb tots els seus punts iguals, és a dir, amb secció constant. Tirem dels extrems, ho tallem? Si és així, on es detindrà? Recorda que no té punts més febles que els altres. Se suspendrà en tots els punts?

2. Sóc capicua, tinc un únic divisor entre 2 i 10, tinc quatre xifres, hi ha qui em veu com 9. Quin número sóc?.

3. Quin d'aquestes dues seqüències no és adequada?

4t En una taula de dames cal col·locar 13 fitxes perquè una dama contrària les mengi en una única jugada. Si ha estat fàcil, aquesta vegada el moviment de la dama comença i acaba en el mateix requadre.

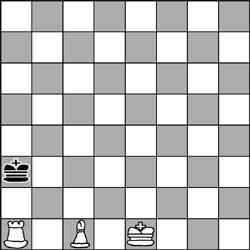
5. Encara que sembli mentida, tant la torre com el perfil estan donant escacs al rei. La posició d'aquesta partida d'escacs és correcta. Quin ha estat l'últim moviment dels blancs?.

6è Per què és més fàcil apagar una espelma bufant que aspirant? (en tots dos casos amb la mateixa força).

7. A cada costat d'una balança hi ha un baldi ple d'aigua i un pes, amb la balança equilibrada. Si fiques un dit a l'aigua, sense tocar el baldi, es mantindrà l'equilibri?

8è. Quin és el major nombre de districtes que poden estar limitats per cinc rectes? I les quatre circumferències?.

9. Es poden col·locar 14 alfils en la taula d'escacs sense agredir?

10. La imatge lateral està formada per 8 peces d'igual forma i grandària. Com són les peces i com estan col·locades?

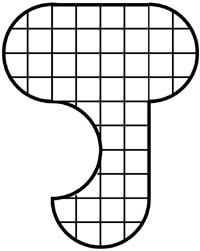
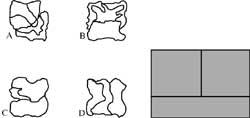
11. Un d'aquests mapes pot convertir-se en una imatge de la dreta. Quin és?.

12. Un artesà vol serrar una galleda per a aconseguir 27 glaçons iguals. Cada cort és correcta, podent acumular les parts tallades. Quin és el menor nombre de corts?.

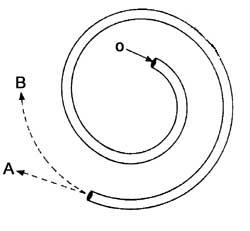
13. Quina direcció se seguirà quan la bola surti del tub?

14. Què mesura 23 polzades en un televisor de 23 polzades?

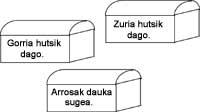
15. Una d'aquestes caixes té un tresor, una altra una serp i la tercera està buida. Sabent que només l'etiqueta de la caixa amb el tresor és certa, en quina caixa està el tresor?.

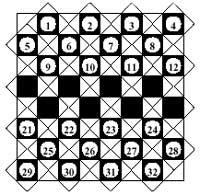
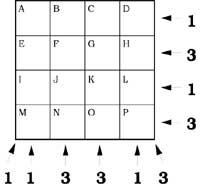
16. En aquesta taula d'escacs les lletres J, K, L, M i N són el rei, la dama, la torre, l'alfila i el cavall (no en aquest ordre). Els números que apareixen en diverses caselles indiquen el nombre de peces que ataquen la casella. Endevina quina peça és cada lletra.

17. El número 43 és especial, ja que compleix 43 = 42 ⁺ 33. Hi ha un únic número de dues xifres amb la mateixa propietat (el número és el quadrat de la primera xifra i la suma del cub de la segona). Quin és?.

18. Quin és el camí més curt del rei negre per a arribar a l'altre vèrtex negre de la taula?. El rei es mou només, pot menjar les peces que desitgi, però no es pot ficar els escacs.

19. Els números 17 i 18 tenen una propietat especial:

173 ⁼ 4913 i 4 + 9 + 1 + 3 = 17183 =
5832 ⁱ 5 + 8 + 3 + 2 = 18

Molt a prop hi ha altres dos números amb la mateixa propietat. Quins són?.

20. Al poble tenen un curiós sistema monetari. Tenen dues monedes de valor: 10 i 7. La nostra pregunta també és curiosa. No obstant això, té una solució senzilla: quina és la major quantitat que no es pot pagar exactament amb aquestes monedes?.

21. Els números 100 i 164 tenen una característica comuna, és a dir, sumant 125 als dos s'obtenen 225 i 289, que són els antics quadrats dels números 15 i 17. Quin altre número es pot afegir als números 100 i 164 per a obtenir altres dos quadrats concrets?.

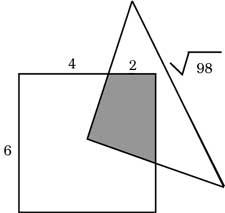
22. En la imatge se situa el vèrtex del triangle isòsceles en el centre del quadrat. Quina és la superfície traçada?.

23. En un restaurant un amic va trobar una mosca en el seu cafè. Va cridar al servidor i li va demanar que porti un altre. Res més beure un doll, va cridar “Aquesta tassa és la mateixa!”. Com es va adonar?.

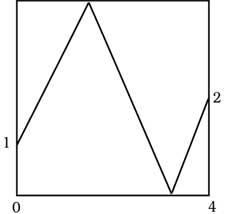
24. En la imatge una pilota parteix del punt de coordenades (0,1) i finalitza el recorregut en el punt (4,2). En quin punt sonarà en les parts superior i inferior.

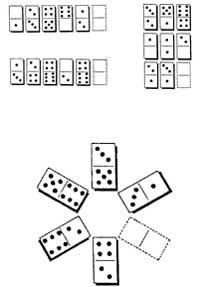
25. En el joc de dominó sabem com unir les fitxes. Per exemple, les fitxes 2-3 i 3-4 s'uneixen mitjançant 3. En aquesta ocasió volem agafar dues fitxes de dominó per a ajuntar-nos. De quantes formes diferents podem aconseguir?.

26. Completa amb totes les xifres de l'1 al 9 la diferència entre dos números de nou xifres (sense repetir xifres) per a obtenir un número format per nou xifres diferents.

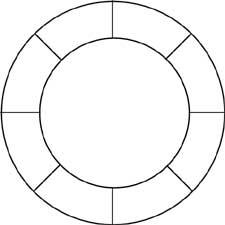
27. Col·loca en la roda lateral els números de l'1 al 8 de la següent manera: suma de les següents de 4, suma de les següents de 9, 5, suma de les següents de 11, 6, perquè la suma de 10 i 7 siguin 8.

28. Saps quin és l'últim número d'aquesta sèrie? : 2, 2, 6, 5, 8, 8, 4, ? ...

29. Dues parelles juguen un partit en les cartes. Es reparteixen 40 cartes cada 10. Què és més fàcil, que a una parella li toquin tots els oro o que no li toqui un or?

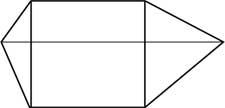
30. Construir una piràmide amb dues peces com la de la imatge.

31. Prenguem el número 8476 i fem el següent procés:

8.4.7.6 = 1344; 1.3.4.4 = 48;4.8
= 32; 3.2 = 6

Mitjançant aquest procés, descobreix els dos números consecutius més petits que donen el mateix resultat (6 o un altre). Similar però ara els tres números petits consecutius.

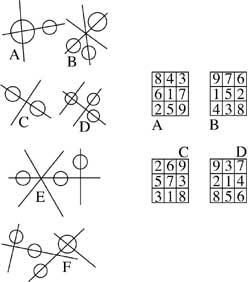
32. Quines són les fitxes que falten en els següents passos:

33. Tenim un quadrat i volem dividir-lo en triangles aguts. Saps com? I per a dividir-nos en triangles desafiaments, què hauríem de fer?.

34. A través de quatre rectes, sense aixecar el llapis, representades l'una després de l'altra. Els 9 punts de la imatge Bildu (es considerarà que els punts són adimensionals).

35. Què veus en la imatge?. No cedeixis tan ràpid!, perquè ho has vist moltes vegades.

36. Joc de globus:

• Agafa, però només dotze —va dir Nagore mostrant les bales de la caixa—. Tenim menys verd que el blau i menys blau que el vermell. Per tant, que cadascun prengui el major nombre possible de vermells i de verds.
• Tots hem tret combinacions diferents —va dir Ainhoa—. Jo sóc l'únic que ha tret quatre bales blaves.
• I? —Hasier va rebre una de les bales verdes que li va caure—. Jugarem. En total hi havia 26 bales vermelles. Quants nens hi havia?.

37è Es col·locaran fitxes en la taula annexa. Els números que apareixen en els costats indiquen el nombre de fitxes en files, columnes o diagonals.

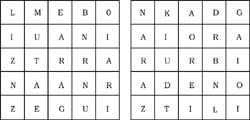
38è Troba 14 pobles bascos (esquerra) i 10 rius (dreta). Les lletres dels noms han d'estar juntes, per vèrtexs o per parts.

39. En el producte contigu tots els asteriscos són els primers números, però què?.

40. Al llarg de la carretera se succeeixen quatre pobles. Els vermells viuen al costat dels verds, però no al costat dels blancs, els blaus no viuen al costat dels blancs. Quins són els barris dels blancs? :

• Vermells
• Verds
• Vermells i verds
• No se sap