Mélange IV
1992/07/01 Angulo, Patxi Iturria: Elhuyar aldizkaria
Il semble que lorsque nous approchons de vacances la publication d'une nouvelle collection de troubles devient une coutume. C'est notre intention. Tout au long de l'année, nous aborderons des sujets plus sérieux (comme jusqu'à présent) et dans le numéro de juillet-août, dans le but de détendre l'esprit ou de lancer une collection comme celle-ci. Tant que nous ne recevons pas d'avis contraire, nous le ferons. En ce qui concerne le grain de décembre, cependant, nous sommes en ma possession. À cette époque, nous avons aussi des jours libres. Cependant, nous avons le doute que sortir deux collections de ce type dans la même année n'est pas trop. Que pensez-vous ?
D'autre part, nous savons tous des choses comme celles qui apparaissent ici, des jeux, des stries… Nous voulons vous proposer de nous envoyer vos connaissances et votre nom et nous vous promettons que nous les publierons complètement.
Les réponses aux questions qui se posent dans le prochain numéro, à savoir dans le numéro 63. Et pour finir, cette section veut être un lieu d'échange de lecteurs, mais pour cela nous avons besoin de votre collaboration. Encouragez-vous !
1. Celui de Zirano Bergerac l'a posé dans son voyage à la lune. Nous savons que lorsque nous tirons les extrémités d'une corde se brise du point le plus faible. Supposons que nous ayons une corde avec tous ses points égaux, c'est-à-dire avec section constante. Tirons les extrémités, le coupons-nous ? Si oui, où s'arrêtera-t-il ? Rappelez-vous que vous n'avez pas de points plus faibles que les autres. Sera-t-il suspendu à tous les points ?
2. Je suis Capicua, j'ai un seul diviseur entre 2 et 10, j'ai quatre chiffres, certains me voient comme 9. Quel chiffre suis-je?
3. Lequel de ces deux séquences n'est pas approprié?
4º Sur une table de dames il faut placer 13 tuiles pour qu'une dame contraire les mange en un seul coup. Si cela a été facile, cette fois le mouvement de la dame commence et se termine dans le même cadre.
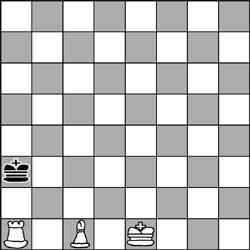
5. Même si cela semble faux, la tour et le profil donnent des échecs au roi. La position de ce jeu d'échecs est correcte. Quel a été le dernier mouvement des blancs?
6º Pourquoi est-il plus facile d'éteindre une bougie en soufflant qu'en aspirant? (dans les deux cas avec la même force).
7. De chaque côté d'une balance il y a un seau rempli d'eau et un poids, avec la balance équilibrée. Si vous mettez un doigt dans l'eau, sans toucher le seau, l'équilibre sera-t-il maintenu ?
8º. Quel est le plus grand nombre de districts qui peuvent être limités par cinq droites? Et les quatre circonférences?.
9. Pouvez-vous placer 14 alfiles sur le tableau d'échecs sans agresser?
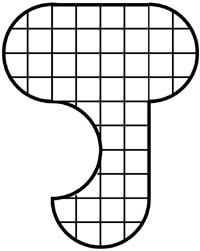
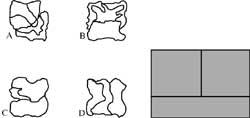
10. L'image latérale est composée de 8 pièces de même forme et taille. Comment sont les pièces et comment sont-elles placées ?

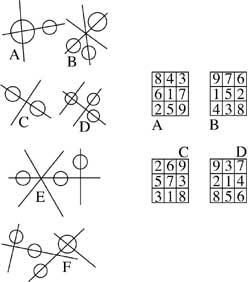
11. Une de ces cartes peut devenir une image à droite. Qu'est-ce que c'est ?
12. Un artisan veut scier un cube pour obtenir 27 cubes égaux. Chaque coupe est correcte, pouvant accumuler les parties coupées. Quel est le plus petit nombre de coupes?
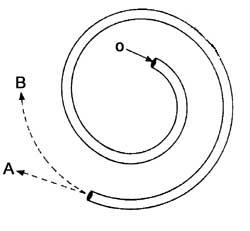
13. Quelle direction suivra lorsque la balle quitte le tube?
14. Que mesure 23 pouces sur un téléviseur de 23 pouces ?
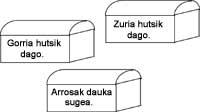
15. Une de ces boîtes a un trésor, une autre un serpent et la troisième est vide. Sachant que seule l'étiquette de la boîte avec le trésor est certaine, dans quelle boîte est le trésor?.
16. Dans ce tableau d'échecs les lettres J, K, L, M et N sont le roi, la dame, la tour, la rangée et le cheval (pas dans cet ordre). Les chiffres affichés dans plusieurs cases indiquent le nombre de pièces attaquant la case. Devinez quelle pièce est chaque lettre.

17. Le numéro 43 est spécial car il correspond à 43 = 42 + 33. Il y a un seul nombre de deux chiffres avec la même propriété (le nombre est le carré du premier chiffre et la somme du cube du second). Qu'est-ce que c'est ?
18. Quel est le chemin le plus court du roi noir pour atteindre l'autre sommet noir de la table?. Le roi se déplace seul, peut manger les pièces que vous voulez, mais vous ne pouvez pas mettre les échecs.

19. Les numéros 17 et 18 ont une propriété spéciale:
173 = 4913 et 4 + 9 + 1 + 3 = 17183 = 5832 et 5 + 8 + 3 + 2 = 18
A proximité il y a deux autres numéros avec la même propriété. Quels sont-ils?
20. Dans le village, ils ont un curieux système monétaire. Ils ont deux pièces de valeur: 10 et 7. Notre question est également curieuse. Cependant, vous avez une solution simple: Quelle est la plus grande quantité que vous ne pouvez pas payer exactement avec ces pièces?.
21. Les nombres 100 et 164 ont une caractéristique commune, c'est-à-dire en additionnant 125 aux deux on obtient 225 et 289, qui sont les anciens carrés des numéros 15 et 17. Quel autre numéro peut être ajouté aux numéros 100 et 164 pour obtenir deux autres carrés concrets?
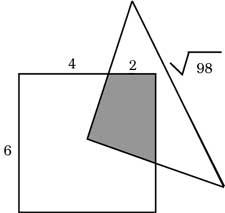
22. Sur l'image se trouve le sommet du triangle isocèle au centre du carré. Quelle est la surface tracée?
23. Dans un restaurant un ami a trouvé une mouche dans son café. Il a appelé le serveur et lui a demandé d'en apporter un autre. Dès qu’il eut bu un jet, il cria: «Cette tasse est la même!» Comment avez-vous réalisé?
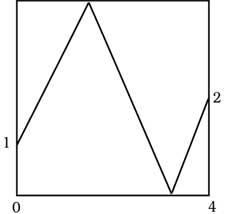
24. Sur l'image une balle part du point de coordonnées (0,1) et termine le parcours au point (4,2). À quel point il sonnera dans les parties supérieure et inférieure.
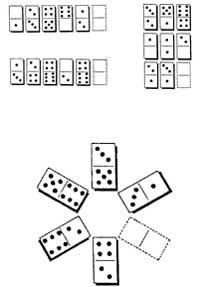
25. Dans le jeu de dominos, nous savons comment joindre les tuiles. Par exemple, les tuiles 2-3 et 3-4 sont reliées par 3. Cette fois, nous voulons prendre deux dominos pour nous rejoindre. Combien de formes différentes pouvons-nous obtenir?
26. Compléter avec tous les chiffres de 1 à 9 la différence entre deux nombres à neuf chiffres (sans répéter les chiffres) pour obtenir un nombre composé de neuf chiffres différents.
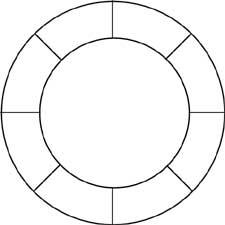
27. Placez sur la roue latérale les numéros de 1 à 8 comme suit : somme des 4 suivants, somme des 9, 5 suivants, somme des 11, 6 suivants, pour que la somme de 10 et 7 soient 8.
28. Savez-vous quel est le dernier numéro de cette série? : 2, 2, 6, 5, 8, 8, 4, ? ...
29. Deux couples jouent un match dans les cartes. Chaque 10, 40 cartes sont distribuées. Qu'est-ce qui est plus facile, qu'un couple touche tous l'or ou ne touche pas un or ?
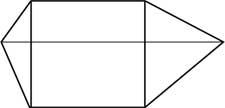
30. Construire une pyramide avec deux pièces comme celle de l'image.
31. Prenons le numéro 8476 et faisons le processus suivant:
8.4.7.6 = 1344; 1.3.4.4 = 48;4.8 = 32; 3.2 = 6
Grâce à ce processus, découvrez les deux plus petits numéros consécutifs qui donnent le même résultat (6 ou autre). Semblable mais maintenant les trois petits nombres consécutifs.
32. Quels sont les jetons manquants dans les étapes suivantes:
33. Nous avons un carré et nous voulons le diviser en triangles aigus. Savez-vous comment? Et pour nous diviser en triangles défis, que devrions-nous faire ?

34. À travers quatre droites, sans soulever le crayon, représentées l'une après l'autre. Les 9 points de l'image Bildu (les points sont considérés comme adimensionaux).

35. Que vois-tu dans l'image ? Ne cédez pas si vite!, parce que vous l'avez vu plusieurs fois.

36. Jeu de ballons:
- Il prend, mais seulement douze — a dit Nagore montrant les billes de la boîte —. Nous avons moins de vert que le bleu et moins de bleu que le rouge. Par conséquent, que chacun prenne le plus grand nombre possible des rouges et des verts.
- Nous avons tous tiré des combinaisons différentes — a dit Ainhoa. Je suis le seul qui a sorti quatre billes bleues.
- Et ? —Hasier reçut une des billes vertes qui lui tomba. Nous allons jouer. Au total, il y avait 26 billes rouges. Combien d'enfants avait-il?
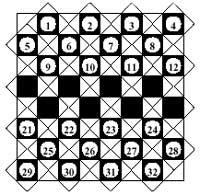
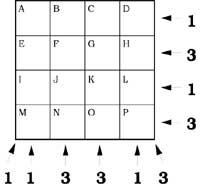
37º Les tuiles seront placées dans la table annexe. Les nombres qui apparaissent sur les côtés indiquent le nombre de tuiles en rangées, colonnes ou diagonales.
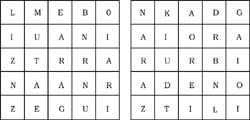
38ème Trouvez 14 villages basques (à gauche) et 10 rivières (à droite). Les lettres des noms doivent être jointes, par sommets ou par parties.
39. Dans le produit contigu tous les astérisques sont les premiers numéros, mais quoi?.

40. Le long de la route se succèdent quatre villages. Les rouges vivent à côté des verts, mais pas à côté des blancs, les bleus ne vivent pas à côté des blancs. Quels sont les quartiers blancs ? :
- Rouges
- Verts
- Rouges et verts
- On ne sait pas

Gai honi buruzko eduki gehiago
Elhuyarrek garatutako teknologia