Mesturado IV

1992/07/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

Parece que cando nos achegamos a unhas vacacións a publicación dunha nova colección de desordes está a converterse nun costume. Esa é a nosa intención. Ao longo do ano abordaremos temas máis serios (como até agora) e no número de xullo-agosto, co obxectivo de relaxar a mente ou lanzar una colección como esta. Mentres non recibamos ningunha opinión en contra, farémolo así. Respecto ao gran de decembro, con todo, estamos no meu poder. Nesta época tamén temos días libres. Con todo, temos a dúbida de que sacar dúas coleccións deste tipo no mesmo ano non é demasiado. Que opinas?

Doutra banda, todos sabemos cousas como as que aparecen aquí, xogos, raias… Queremos propornos que nos envíes os teus coñecementos e o teu nome e prometémosche que os publicaremos completamente.

As respostas ás preguntas que se expoñen no seguinte número, é dicir, no número 63. E paira terminar, este apartado quere ser un lugar de intercambio de lectores, pero paira iso necesitamos a túa colaboración. Anímache!.

1. O de Zirano Bergerac expúxoo na súa viaxe á lúa. Sabemos que cando tiramos dos extremos dunha corda rompe do punto máis débil. Supoñamos que temos una corda con todos os seus puntos iguais, é dicir, con sección constante. Tiremos dos extremos, cortámolo? Si é así, onde se deterá? Lembra que non ten puntos máis débiles que os demais. Suspenderase en todos os puntos?

2. Son capicua, teño un único divisor entre 2 e 10, teño catro cifras, hai quen me ve como 9. Que número son?.

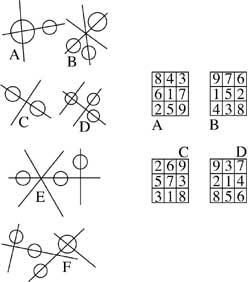
3. Cal destas dúas secuencias non é adecuada?

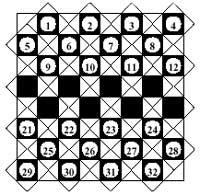
4º Nunha táboa de damas hai que colocar 13 fichas para que una dama contraria cómaas nunha única xogada. Se foi fácil, esta vez o movemento da dama comeza e termina no mesmo recuadro.

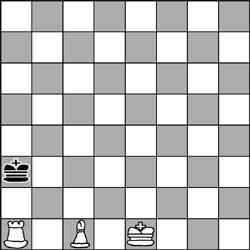
5. Aínda que pareza mentira, tanto a torre como o perfil están a dar xadrez ao rei. A posición desta partida de xadrez é correcta. Cal foi o último movemento dos brancos?.

6º Por que é máis fácil apagar una vea soprando que aspirando? (en ambos os casos coa mesma forza).

7. A cada lado dunha balanza hai un balde cheo de auga e un peso, coa balanza equilibrada. Se metes un dedo á auga, sen tocar o balde, manterase o equilibrio?

8º. Cal é o maior número de distritos que poden estar limitados por cinco rectas? E as catro circunferencias?.

9. Pódense colocar 14 alfiles na táboa de xadrez sen agredir?

10. A imaxe lateral está formada por 8 pezas de igual forma e tamaño. Como son as pezas e como están colocadas?

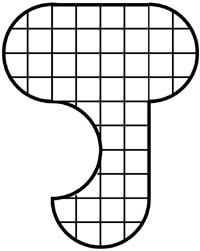
11. Uno destes mapas pode converterse nunha imaxe da dereita. Cal é?.

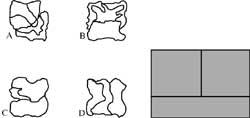
12. Un artesán quere aserrar un cubo paira conseguir 27 cubitos iguais. Cada corte é correcto, podendo acumular as partes cortadas. Cal é o menor número de cortes?.

13. Que dirección seguirase cando a bóla salga do tubo?

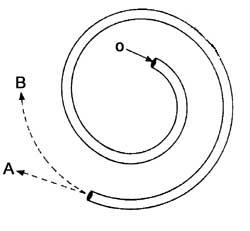
14. Que mide 23 polgadas nun televisor de 23 polgadas?

15. Una destas caixas ten un tesouro, outra una serpe e a terceira está baleira. Sabendo que só a etiqueta da caixa co tesouro é certa, en que caixa está o tesouro?.

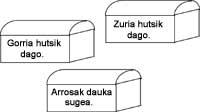
16. Nesta táboa de xadrez as letras J, K, L, M e N son o rei, a dama, a torre, o alfila e o cabalo (non nesta orde). Os números que aparecen en varias casas indican o número de pezas que atacan a casa. Adiviña que peza é cada letra.

17. O número 43 é especial, xa que cumpre 43 = 42 ⁺ 33. Hai un único número de dúas cifras coa mesma propiedade (o número é o cadrado da primeira cifra e a suma do cubo da segunda). Cal é?.

18. Cal é o camiño máis curto do rei negro paira chegar ao outro vértice negro da táboa?. O rei móvese só, pode comer as pezas que desexe, pero non se pode meter o xadrez.

19. Os números 17 e 18 teñen una propiedade especial:

173 ⁼ 4913 e 4 + 9 + 1 + 3 = 17183 =
5832 ^e 5 + 8 + 3 + 2 = 18

Moi preto hai outros dous números coa mesma propiedade. Cales son?.

20. No pobo teñen un curioso sistema monetario. Teñen dúas moedas de valor: 10 e 7. A nosa pregunta tamén é curiosa. Con todo, ten una solución sinxela: cal é a maior cantidade que non se pode pagar exactamente con estas moedas?.

21. Os números 100 e 164 teñen una característica común, é dicir, sumando 125 aos dous obtéñense 225 e 289, que son os antigos cadrados dos números 15 e 17. Que outro número se pode engadir aos números 100 e 164 paira obter outros dous cadrados concretos?.

22. Na imaxe sitúase o vértice do triángulo isósceles no centro do cadrado. Cal é a superficie trazada?.

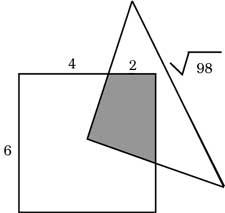
23. Nun restaurante un amigo atopou una mosca no seu café. Chamou ao servidor e pediulle que traia outro. Nada máis beber un chorro, gritou “Esta cunca é a mesma!”. Como se deu conta?.

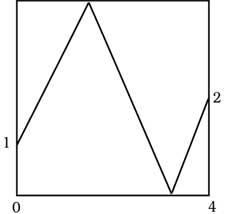
24. Na imaxe una pelota parte do punto de coordenadas (0,1) e finaliza o percorrido no punto (4,2). En que punto soará nas partes superior e inferior.

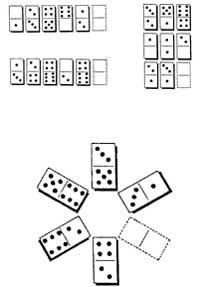
25. No xogo de dominou sabemos como unir as fichas. Por exemplo, as fichas 2-3 e 3-4 únense mediante 3. Nesta ocasión queremos coller dúas fichas de dominou paira xuntarnos. De cantas formas diferentes podemos conseguir?.

26. Completa con todas as cifras do 1 ao 9 a diferenza entre dous números de nove cifras (sen repetir cifras) paira obter un número formado por nove cifras diferentes.

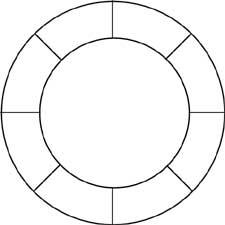
27. Coloca na roda lateral os números do 1 ao 8 da seguinte maneira: suma das seguintes de 4, suma das seguintes de 9, 5, suma das seguintes de 11, 6, para que a suma de 10 e 7 sexan 8.

28. Sabes cal é o último número desta serie? : 2, 2, 6, 5, 8, 8, 4, ? ...

29. Dúas parellas xogan un partido nas cartas. Repártense 40 cartas cada 10. Que é máis fácil, que a unha parella tóquenlle todos o ouro ou que non lle toque un ouro?

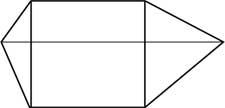
30. Construír una pirámide con dúas pezas como a da imaxe.

31. Tomemos o número 8476 e fagamos o seguinte proceso:

8.4.7.6 = 1344; 1.3.4.4 = 48;4.8
= 32; 3.2 = 6

Mediante este proceso, descobre os dous números consecutivos máis pequenos que dan o mesmo resultado (6 ou outro). Similar pero agora os tres números pequenos consecutivos.

32. Cales son as fichas que faltan nos seguintes pasos:

33. Temos un cadrado e queremos dividilo en triángulos agudos. Sabes como? E paira dividirnos en triángulos desafíos, que deberiamos facer?.

34. A través de catro rectas, sen levantar o lapis, representadas una tras outra. Os 9 puntos da imaxe Bildu (considerarase que os puntos son adimensionais).

35. Que ves na imaxe?. Non cedas tan rápido!, porque o viches moitas veces.

36. Xogo de globos:

• Colle, pero só doce —dixo Nagore mostrando as canicas da caixa—. Temos menos verde que o azul e menos azul que o vermello. Por tanto, que cada un tome o maior número posible de vermellos e de verdes.
• Todos sacamos combinacións diferentes —dixo Ainhoa—. Eu son o único que sacou catro canicas azuis.
• E? —Hasier recibiu una das canicas verdes que caeu—. Imos xogar. En total había 26 canicas vermellas. Cantos nenos había?.

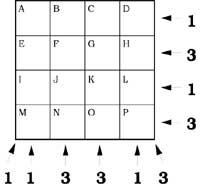
37º Colocaranse fichas na táboa anexa. Os números que aparecen nos lados indican o número de fichas en filas, columnas ou diagonais.

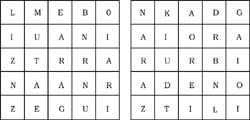
38º Atopa 14 pobos vascos (esquerda) e 10 ríos (dereita). As letras dos nomes deben estar xuntas, por vértices ou por partes.

39. No produto contiguo todos os asteriscos son os primeiros números, pero que?.

40. Ao longo da estrada sucédense catro pobos. Os vermellos viven xunto aos verdes, pero non xunto aos brancos, os azuis non viven xunto aos brancos. Cales son os barrios dos brancos? :

• Vermellos
• Verdes
• Vermellos e verdes
• Non se sabe