Desordre

1989/04/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

Comencem per tant amb el següent test:

1. Es trien a l'atzar tres punts d'una esfera. Quina és la probabilitat que els tres punts estiguin en el mateix hemisferi? (Es pot considerar que els punts que el cercle màxim que delimita l'hemisferi, per exemple l'equador, té en el seu interior, pertanyen a qualsevol dels dos hemisferis).

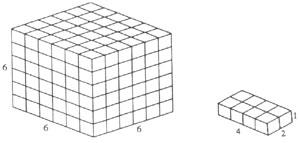
2. Es pot completar un cub de 6x6x6 amb vint maons de 1x2x4 dimensions? (Veure figura 1).

3. Un lògic, que havia de passar el temps en una ciutat, va decidir anar a una perruqueria. A la ciutat només hi havia dues perruqueries. Es va dirigir a un d'ells. Allí va veure coses desordenades: el propi propietari portava roba bruta, tenia una barba d'uns dies i el pèl destrossat. No va trigar a traslladar-se. En aquesta ocasió tot estava ben ordenat. Elegant perruquer sense barbes i ben pentinat. Lògic, res més veure-ho, va tornar a la primera. Per què?

4t Observa les cinc imatges de poxpóker (figura 2).

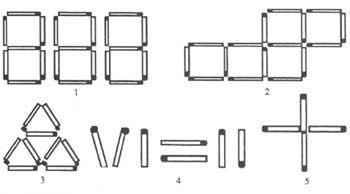
1. Llevant nou poxpolos, deixa sis.

2. Canviant dos poxpolos de lloc, deixa els cinc quadrats per quatre (tots els poxpolos han d'estar en algun costat d'un quadrat).

3. Eliminant quatre, tres o dos poxpolos d'aquesta imatge, es poden obtenir dos triangles equilàters. Com?

4t Feix realitat aquesta igualtat movent un sol poxpolu.

5. Completa un quadrat movent un només escalfi en aquesta creu. (No serveix moure un parell de mil·límetres un poxpulo perquè els quatre extrems formin un quadrat buit)

5. Suposem que tenim sis boles de la mateixa grandària: dues vermelles, dues negres i dues blanques. En cada parella una bola és més pesada que l'altra. Les tres boles pesades tenen el mateix pes i les tres lleugeres també. Fent només dos pesos amb una balança, com es pot diferenciar el pesat en cada parella?

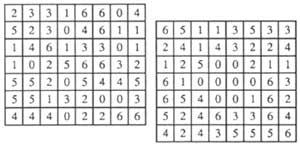
6è He aquí (Figura 3) els dámeros numèrics. En aquests 7 x 8 rectangles es troben disperses vint-i-vuit fitxes de dominó. A veure si les trobes (la de l'esquerra té una única solució, l'altra té vuit solucions diferents i per això és més difícil).

7. Un ramader té 20 porcs, 40 vaques i 60 cavalls. Però si diem vaques als cavalls, quantes vaques tindrà?

8è. Construeix vuit triangles equilàters dibuixant sis rectes de la mateixa longitud.

9. Presa deu monedes. Amb aquestes deu monedes has de formar cinc línies rectes de quatre monedes.

10. Dibuixa una línia recta i agafa tres monedes. Col·loca aquestes tres monedes perquè quedin dues cares a un costat de la línia i dues creus senceres a un altre.

11. Si un ferro similar al “dònuts” es posa a escalfar, augmentarà o disminuirà el diàmetre del forat?

12. Quin és el número més gran que es pot escriure posant només 2 xifres tres vegades?

13. Hem fet un volt completa al gran cercle que es veu en la figura 4. Per tant, la longitud de la seva circumferència serà PQ. Al mateix temps hem fet un volt al cercle interior, sent la longitud de la seva circumferència RS. Com explicaria la raó que les longituds d'aquestes dues circumferències fossin iguals?

14. El cretano Epimenides va dir: tots els cretencs són mentiders. Què pots dir d'aquesta frase?

15. Protàgores va fer un pacte amb un alumne seu. Segons l'acord, l'alumne havia de pagar els estudis quan va guanyar el seu primer cas. En finalitzar l'alumne no va tenir sort i no va trobar clients durant molt de temps. Protàgores, preocupat, va denunciar al seu estudiant. Protàgores va argumentar en el judici que si jo guanyo el plet m'hauria de pagar per a complir la sentència. Per contra, si ganes, m'hauré de pagar segons el nostre acord. Per tant, m'hauré de pagar en qualsevol cas. Però l'alumne no estava d'acord i li va contestar: si guanyes tu, respectant el nostre pacte no hauràs de pagar i si guanyo jo, els jutges no m'obligaran a pagar. Pel que en cap cas haig de pagar. Quin és el raonament correcte?

16. Amb el cavall d'escacs emplena els següents quadrats sense passar dues vegades per cada casella. (Figura 5).

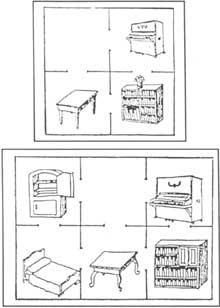
17. A continuació es presenten dos problemes de translació. En tots dos casos se suposa que només s'introdueix un moble en cada habitació i en tots dos casos els amos volen traslladar el piano i la biblioteca, passant el piano a la sala on està la biblioteca i viceversa. Com hauran d'actuar amb els menors canvis possibles? (Figura 6).

18. Als amics A, B i C se'ls ensenyen tres cintes blanques i dues cintes negres. Després penja una cinta a l'esquena de cadascun. Cada persona pot veure les cintes dels altres, però no la seva. Cadascun ha d'endevinar quin color porta a l'esquena. El seu amic A veu que les cintes dels altres són blanques. Passats uns minuts sense que ningú digués, A va donar la resposta correcta. Quina és la resposta i com la va raonar?

19. Un comerciant té quatre peces o pesos. Amb aquests pesos es poden realitzar totes les pesades d'1 a 40 kg. per quilo. Quins pesos té?

20. Vaig donar, agut, tres números els productes i les sumes dels quals són iguals.

21. Bittori i Itziar volen agafar el tren dels onze. El rellotge de Bittori està retardat 10 minuts, però ell creu que està avançat 5 minuts. El rellotge d'Itziar, en canvi, està 5 minuts avançat, però ell creu que 10 minuts està retardat. Quin arribarà a la primera parada?

22. En una biblioteca, situada d'esquerra a dreta, hi ha tres llibres. El primer consta de 340 pàgines, el segon de 400 i el tercer de 350. Una pipa comença a menjar-se des de la primera pàgina del primer exemplar fins a l'última de la tercera. Quantes fulles travessarà el corc?

23. Cementiri o epitafi de Diofanto: Compte Diofanto amb la tomba en la qual apareixen les diferents etapes de la seva vida: en la seva infància va donar la sisena part de la seva vida; a partir d'aquí, la dotzena part fins que la barba va començar a omplir les galtes; a partir de llavors, la setena, fins que es va casar; cinc anys després del seu matrimoni va néixer el seu fill; després, quan va arribar a la meitat de l'edat del seu pare, va morir imprevisiblement; el seu pare va plorar quatre estius. Per aquest motiu puguis imaginar la seva edat.

24. Agafa cinc monedes. Col·loca tres cares cap amunt i les altres dues amb la creu cap amunt (AGAGA). Has d'aconseguir deixar les tres cares a un costat i les creus a un altre (AAAGG o GGAAA). Per a això sempre has de moure dues monedes: una cara i l'altra creu (AG o GA). (El buit que queda després d'un moviment no es pot omplir mitjançant la unió de monedes, és a dir, si es fa AGAGAÆA_ _GAGA, no es pot fer després A F AGAGA, però sí AAGG_ _A).

25. La bola que està en una bossa pot ser blanca o negra. S'ha ficat una bola blanca a la bossa i després de treure-la s'ha tret una bola que és blanca. Quina és la probabilitat que la bola que queda en la bossa sigui blanca quan sali? (Lewis Carroll).

26. En una bossa hi ha diverses boles blanques i negres (almenys una de cadascuna). Les boles sortiran de la següent manera: s'agafa una bola, s'apunta el seu color i es rebutja. Si surt una segona bola i és del color de l'anterior, es descartarà. Es prendrà la tercera, si torna a ser del mateix color es descartarà i així successivament fins a aconseguir una bola d'un altre color. Quan surti una bola diferent, es fica en la bossa i una vegada agitada es reprendrà l'extracció. Per exemple:

Negre en 1a sortida: Rebutjar en 2a sortida el negre: rebutjar en 3a sortida el blanc: ficar en bossa

Blanco en la sortida 4: rebutjar en la sortida 5 el negre: ficar en la bossa

Blanco en la sortida 6: rebutjar en la sortida 7 el blanc: rebutjar en la sortida 8 el negre: ficar en la bossa

No importa la situació inicial. L'última bola que queda en la bossa té la mateixa probabilitat de ser negra. Quina és aquesta probabilitat?