Desorde

1989/04/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

Comecemos por tanto co seguinte test:

1. Elíxense ao azar tres puntos dunha esfera. Cal é a probabilidade de que o tres puntos estean no mesmo hemisferio? (Pódese considerar que os puntos que o círculo máximo que delimita o hemisferio, por exemplo o ecuador, ten no seu interior, pertencen a calquera dos dous hemisferios).

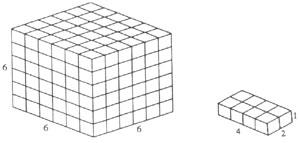
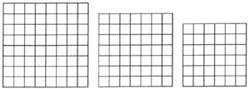
2. Pódese completar un cubo de 6x6x6 con vinte ladrillos de 1x2x4 dimensións? (Ver figura 1).

3. Un lóxico, que tiña que pasar o tempo nunha cidade, decidiu ir a unha barbaría. Na cidade só había dúas barbarías. Dirixiuse a un deles. Alí viu cousas desordenadas: o propio propietario levaba roupa sucia, tiña una barba duns días e o pelo esnaquizado. Non tardou en trasladarse. Nesta ocasión todo estaba ben ordenado. Elegante perruqueiro sen barbas e ben peiteado. Lóxico, nada máis velo, volveu á primeira. Por que?

4º Observa as cinco imaxes de poxpóker (figura 2).

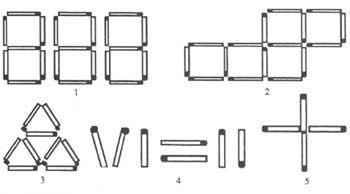
1. Quitando nove poxpolos, deixa seis.

2. Cambiando dous poxpolos de sitio, deixa o cinco cadrados por catro (todos os poxpolos deben estar nalgún lado dun cadrado).

3. Eliminando catro, tres ou dous poxpolos desta imaxe, pódense obter dous triángulos equiláteros. Como?

4º Fai realidade esa igualdade movendo un só poxpolu.

5. Completa un cadrado movendo un só poche nesta cruz. (Non serve mover un par de milímetros un poxpulo para que o catro extremos formen un cadrado baleiro)

5. Supoñamos que temos seis bólas do mesmo tamaño: dúas vermellas, dúas negras e dúas brancas. En cada parella una bóla é máis pesada que a outra. As tres bólas pesadas teñen o mesmo peso e o tres lixeiras tamén. Facendo só dous pesos cunha balanza, como se pode diferenciar o pesado en cada parella?

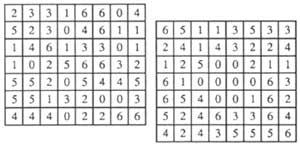
6º Velaí (Figura 3) os dámeros numéricos. Nestes 7 x 8 rectángulos atópanse dispersas vinte e oito fichas de dominou. A ver si atópalas (a da esquerda ten una única solución, a outra ten oito soluciones diferentes e por iso é máis difícil).

7. Un gandeiro ten 20 porcos, 40 vacas e 60 cabalos. Pero si chamamos vacas aos cabalos, cantas vacas terá?

8º. Constrúe oito triángulos equiláteros debuxando seis rectas da mesma lonxitude.

9. Toma dez moedas. Con estas dez moedas tes que formar cinco liñas rectas de catro moedas.

10. Debuxa una liña recta e colle tres moedas. Coloca estas tres moedas para que queden dúas caras ao carón da liña e dúas cruces enteiras a outro.

11. Si un ferro similar ao “donuts” ponse a quentar, aumentará ou diminuirá o diámetro do buraco?

12. Cal é o número máis grande que se pode escribir pondo só 2 cifras tres veces?

13. Demos una volta completa ao gran círculo que se ve na figura 4. Por tanto, a lonxitude da súa circunferencia será PQ. Ao mesmo tempo demos una volta ao círculo interior, sendo a lonxitude da súa circunferencia RS. Como explicaría a razón de que as lonxitudes destas dúas circunferencias fosen iguais?

14. O cretano Epimenides dixo: todos os cretenses son mentireiros. Que podes dicir desta frase?

15. Protágoras fixo un pacto cun alumno seu. Segundo o acordo, o alumno tiña que pagar os estudos cando gañou o seu primeiro caso. Ao finalizar o alumno non tivo sorte e non atopou clientes durante moito tempo. Protágoras, preocupado, denunciou ao seu estudante. Protágoras argumentou no xuízo que si eu gaño o preito teríame que pagar paira cumprir a sentenza. Pola contra, si gañas, tereime que pagar segundo o noso acordo. Por tanto, tereime que pagar en calquera caso. Pero o alumno non estaba de acordo e contestoulle: si gañas ti, respectando o noso pacto non terás que pagar e si gaño eu, os xuíces non me obrigarán a pagar. Polo que en ningún caso debo pagar. Cal é o razoamento correcto?

16. Co cabalo de xadrez enche os seguintes cadrados sen pasar dúas veces por cada casa. (Figura 5).

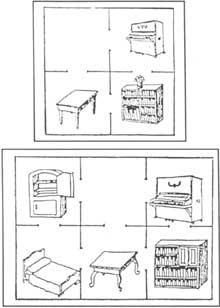
17. A continuación preséntanse dous problemas de translación. En ambos os casos suponse que só se introduce un moble en cada habitación e en ambos os casos os donos queren trasladar o piano e a biblioteca, pasando o piano á sala onde está a biblioteca e viceversa. Como deberán actuar cos menores cambios posibles? (Figura 6).

18. Aos amigos A, B e C ensínanselles tres cintas brancas e dúas cintas negras. Logo colga una cinta nas costas de cada un. Cada persoa pode ver as cintas dos demais, pero non a súa. Cada un debe adiviñar que cor leva nas costas. O seu amigo A ve que as cintas dos demais son brancas. Pasados uns minutos sen que ninguén dixese, A deu a resposta correcta. Cal é a resposta e como a razoou?

19. Un comerciante ten catro pezas ou pesos. Con estes pesos pódense realizar todas as pesadas de 1 a 40 kg. por quilo. Que pesos ten?

20. Dei, agudo, tres números cuxos produtos e sumas son iguais.

21. Bittori e Itziar queren coller o tren do once. O reloxo de Bittori está atrasado 10 minutos, pero el cre que está adiantado 5 minutos. O reloxo de Itziar, en cambio, está 5 minutos adiantado, pero el cre que 10 minutos está atrasado. Cal chegará á primeira parada?

22. Nunha biblioteca, situada de esquerda a dereita, hai tres libros. O primeiro consta de 340 páxinas, o segundo de 400 e o terceiro de 350. Una pipa comeza a comerse desde a primeira páxina do primeiro exemplar até a última da terceira. Cantas follas atravesará a carcoma?

23. Cemiterio ou epitafio de Diofanto: Conta Diofanto coa tumba na que aparecen as distintas etapas da súa vida: na súa infancia deu a sexta parte da súa vida; a partir de aí, a doceava parte ata que a barba empezou a encher as fazulas; a partir de entón, a sétima, ata que casou; cinco anos despois do seu matrimonio naceu o seu fillo; despois, cando chegou á metade da idade do seu pai, morreu imprevisiblemente; o seu pai chorou catro veráns. Por iso é polo que poidas imaxinar a súa idade.

24. Colle cinco moedas. Coloca tres caras cara arriba e as outras dúas coa cruz cara arriba (AGAGA). Tes que conseguir deixar o tres caras ao carón e as cruces a outro (AAAGG ou GGAAA). Paira iso sempre tes que mover dúas moedas: una cara e a outra cruz (AG ou GA). (O oco que queda despois dun movemento non se pode encher mediante a unión de moedas, é dicir, si faise AGAGAÆA_ _GAGA, non se pode facer logo A F AGAGA, pero si AAGG_ _A).

25. A bóla que está nunha bolsa pode ser branca ou negra. Meteuse una bóla branca á bolsa e tras sacala sacouse una bóla que é branca. Cal é a probabilidade de que a bóla que queda na bolsa sexa branca cando salgue? (Lewis Carroll).

26. Nunha bolsa hai varias bólas brancas e negras (polo menos una de cada una). As bólas sairán da seguinte maneira: cóllese una bóla, apúntase a súa cor e rexéitase. Si salgue una segunda bóla e é da cor da anterior, descartarase. Tomarase a terceira, si volve ser do mesma cor descartarase e así sucesivamente até conseguir una bóla doutra cor. Cando salga una bóla diferente, métese na bolsa e una vez axitada retomarase a extracción. Por exemplo:

Negro en 1ª saída: Refugar en 2ª saída o negro: refugar en 3ª saída o branco: meter en bolsa

Branco na saída 4: refugar na saída 5 o negro: meter na bolsa

Branco na saída 6: refugar na saída 7 o branco: refugar na saída 8 o negro: meter na bolsa

Non importa a situación inicial. A última bóla que queda na bolsa ten a mesma probabilidade de ser negra. Cal é esa probabilidade?