El millor teorema de Noether

2019/12/01 Urizar Lanz, Iñigo - Fisikan doktorea Iturria: Elhuyar aldizkaria

• Historia
• Fisika
• Matematika

Els matemàtics coneixen més d'un teorema de Noether. De fet, el cognom Noether és portat per una famosa família de matemàtics. Però entre tots existeix un teorema de Noether especialment bonic. Emmy és de Noether.

Amalie Emmy Noether va néixer a Alemanya en 1882. Per a molts és la dona matemàtica més gran de la història. Malgrat les dificultats, va aconseguir aprendre matemàtiques (ja que estava prohibit per a les dones de l'època); en estar també prohibit ser professor, va fer classes en substitució del seu amic David Hilbert. En paraules d'Einstein, Noether és el major geni de les matemàtiques des que va començar l'ensenyament superior femení. En 1918, Noether va publicar el seu teorema més famós. Per a molts experts, el teorema més bell i profund que té la física matemàtica.

És bell perquè ens mostra la base dels principis de conservació que es coneixien des de fa temps, fent veure que molts principis diferents tenen la mateixa base. I profunda, perquè combina dues idees que en principi semblen molt diferents: els principis de simetria i conservació.

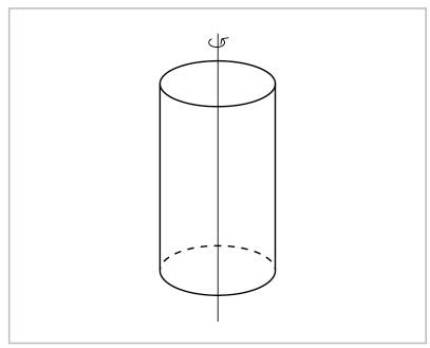
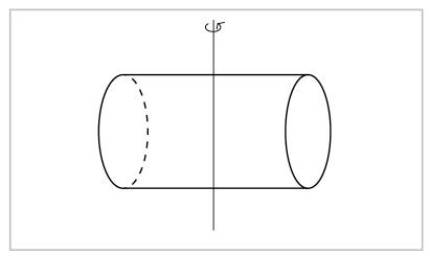
La idea de simetria és molt bàsica: una cosa de simetria la veiem igual abans i després de l'exercici de simetria. Un cilindre, per exemple, el veurem igual si es produeix qualsevol rotació sobre el seu eix. No podem distingir entre el cilindre anterior i el posterior a la rotació.

Si girem al voltant d'un altre eix, per contra, no veurem el cilindre igual. Podem saber si algú ha girat o no.

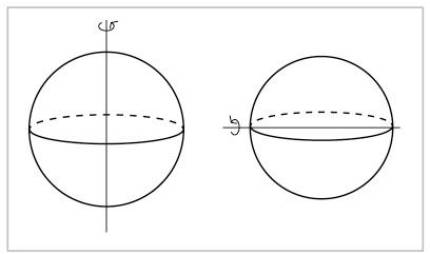
Una esfera és un objecte encara més simètric. Girant al voltant de qualsevol eix que passi pel seu centre, el veurem igual.

Cal esmentar dos tipus de simetria: les simetries contínues i les simetries discretes. En matemàtiques, seguir significa que dos objectes del que s'ha seguit poden estar tan a prop com es vulgui. Per tant, en una simetria contínua, dues operacions de simetria estan molt pròximes entre si. En els casos dels eixos de l'esfera i del cilindre, totes les rotacions són de simetria, encara que siguin mínimes. I hi ha una operació de simetria molt pròxima a una operació de simetria. En la segona figura, perquè una rotació sigui simètrica ha de ser de 180 graus, per la qual cosa molt prop d'una rotació de simetria no hi ha una altra rotació de simetria. Aquesta simetria és discreta.

Un principi de conservació ens diu que el valor d'una magnitud física no varia. Tots hem sentit parlar del principi de conservació de l'energia: l'energia no es pot produir ni destruir. En un sistema físic, l'energia (si està aïllada) no canvia amb el temps. També es coneixien molts altres principis de conservació. a principis del segle XX: principi de conservació del moment lineal i principi de conservació del moment angular, per citar els més importants.

Els físics busquen aquest tipus de principis perquè els ajuden a comprendre millor els seus sistemes. Per exemple, gràcies al principi de conservació de l'energia, som capaces d'explicar per què els planetes van més ràpid en la seva el·lipse al voltant del sol, quan estan més prop del sol que quan estan més lluny (aquest principi dóna una explicació a la famosa llei de Kepler). I per si no fos prou, som capaços d'endevinar la velocitat dels planetes en un punt i un altre. Alguna cosa semblança ocorre amb els àtoms: som capaços de saber el color de llum que emetrà un àtom d'una determinada espècie química, atenent simplement el principi de conservació de l'energia.

El principi de conservació del moment lineal ens permet conèixer la velocitat amb la qual sortiran els objectes col·lidits després d'un xoc. Això pot servir, per exemple, per a conèixer la velocitat dels vehicles en un accident de trànsit o per a controlar els detalls de la col·lisió que va crear el bosó d'Higgs.

La conservació del moment angular té, entre molts altres, una bonica conseqüència: l'òrbita d'un planeta al voltant del sol es troba en un pla. És a dir, un planeta mai pot sortir d'aquest pla. El pla de l'òrbita de la Terra es diu eclíptica. Aquesta paraula serà coneguda pels afeccionats a l'astronomia, ja que és també el nom de la trajectòria del sol en el cel i les constel·lacions del zodíac estan situades en ell. Perquè si no fos pel principi de conservació del moment angular, l'òrbita de la Terra no estaria en l'Eclíptica i es desplaçaria per damunt i per sota d'aquest pla sortint del pla.

XX. A principis del segle XX es coneixien alguns d'aquests principis de conservació. En aquella època, Noether va donar a aquests principis un significat sorprenent. Enunciarem una versió informal del seu teorema:

“Qualsevol simetria contínua d'un sistema respon a un principi de conservació”.

Noether va aportar la demostració del teorema (en aquest article no el donarem perquè és molt tècnic). Per a comprendre millor el significat i la profunditat d'aquesta frase, posem com a exemple les simetries més importants de la física: les simetries del temps espacial.

Abans de començar, què és una simetria del temps espacial? Perquè imaginem un espai buit. L'espai interestel·lar, si volem, on no hi ha gravetat. Quins canvis geomètrics podem fer a aquest espai? Perquè per exemple, podem fer una translació espacial. És a dir, podem moure'ns en qualsevol direcció a certa distància. En física hi ha un principi, anomenat principi de la relativitat, que ens diu que totes les lleis de la física han de ser iguals en aquesta nova posició. Si no fossin iguals, el resultat d'un experiment seria diferent en l'una o l'altra posició. Per exemple, els electrons d'un àtom se situarien de manera diferent a la nostra habitació, a la casa del nostre veí o en la galàxia d'Andrómeda. Mai ho hem vist així, per la qual cosa pensem que les lleis de la física són les mateixes en tots els punts de l'espai i, per tant, els resultats de tots els experiments són els mateixos en qualsevol lloc. Per això diem que és una simetria de l'espai, perquè un punt de l'espai no es pot separar de tots els altres.

El principi de la relativitat ens dóna compte d'altres simetries: mai ningú ha vist una llei de la física que canvia amb el temps. Lleis de l'electricitat, per exemple, el XIX. Es van establir en el segle XIX i avui dia continuen sent idèntiques (anomenades lleis de Maxwell). No s'han modificat. És més, tenim poderoses raons per a pensar que en el passat també han existit diversos milions d'anys de lleis. Aquest fenomen es denomina simetria amb les translacions temporals. Una translació temporal per al passat o per al futur no pot canviar la llei de la física. El resultat d'un experiment serà avui, ahir o demà.

Tenim perquè dues simetries que ens ha donat el principi de la relativitat: les translacions espacials i les translacions temporals. Existeix una tercera simetria que ens dóna el principi de relativitat: la simetria amb les rotacions. Totes les lleis de la física són iguals si prenguéssim tot el sistema i el fem girar. És a dir, l'espai no té una direcció privilegiada, a la qual es mira una física diferent que qualsevol altra direcció.

Per tant, segons el principi de relativitat, l'espai no té lloc privilegiat, no té moment privilegiat i no té direcció privilegiada. El resultat de tot experiment, com el xoc entre dos electrons o l'estat de tres quarks que formen un protó, és idèntic en tots els punts de l'espai, en tots els moments del temps i en totes les direccions de l'espai. Si tanquéssim els ulls i féssim una rotació, una translació temporal o una translació espacial, en cap cas seria possible saber si s'ha produït aquesta operació en reobrir-se. Aquestes són les simetries del temps espacial que estableix el principi de la relativitat (ja que el principi de la relativitat ens dóna compte de més simetries, però no les esmentarem en aquest article per a no confondre massa).

Aquestes tres simetries són contínues. En el cas de les translacions espacials, podem fer una translació molt petita i quedar-nos en un punt molt pròxim. En el cas de les translacions de temps també podem “moure'ns” a un moment molt pròxim (no hi ha salts discontinus en l'espai i en el temps). I triant un eix, podem realitzar una petita rotació al voltant d'aquest. Per tant, en tractar-se de simetries contínues, es pot aplicar el teorema de Noether.

I quines serien les magnituds conservades corresponents a aquestes simetries? Doncs bé, el propi teorema ens diu que en el cas de les translacions espacials, la magnitud que es conserva és el moment lineal. En el cas de les translacions de temps, energia. I en el cas de les rotacions, el moment angular. Quin bon resultat!

Noether va descobrir una relació profunda i sorprenent entre les simetries i els principis de conservació: són conseqüència de l'altra! Tots dos van plegats, no es poden separar. En un món on l'energia no es conservaria, les lleis de la física es desenvoluparien amb el temps, és a dir, s'anirien modificant en el temps. Dos moments diferents del temps no serien inseparables.

Encara que no els hem esmentat en aquest article, ja que hem parlat únicament de les simetries del temps espacial, aquest teorema és aplicable a totes les altres simetries. Per a encuriosir del públic lector direm que la conservació de la càrrega elèctrica també és conseqüència del teorema de Noether. En aquest cas, la simetria no és el temps espacial, sinó el propi sistema d'equacions, i a aquesta simetria més abstracta se'n diu simetria gauge. Això pot incloure una interpretació geomètrica en un espai de més de quatre dimensions. Però això és qüestió de deixar-ho per a un altre dia.

Com va dir Robert Wald, una vegada que s'ha adonat d'això, no pot evitar que un pugui sentir que ha après una cosa molt profunda sobre com actua la naturalesa. Aquest és, per tant, el regal que ens va deixar aquesta gran dona.

Bibliografia