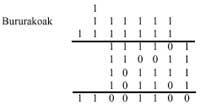
Canvi de base

1989/09/01 Arrojeria, Eustakio - Elhuyar Zientziaren Komunikazioa | Lizaso, Pili - Informatika SailaElhuyar Fundazioa Iturria: Elhuyar aldizkaria

• Programazioa

Amb l'excusa que estàvem en l'últim número a l'estiu, us vam oferir un joc. Per descomptat que després haureu jugat prou i al final de l'estiu hem de tornar a la via. Estem al principi d'un nou curs i és hora de començar a posar en marxa els motors. Esperem que el programa d'aquest número us ajudi en aquest treball.

El sistema normal utilitzat per a representar els números és l'harmático, és a dir, un sistema format per deu signes o dígits diferents (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). De totes maneres, sabreu que els ordinadors treballen en el sistema binari, és a dir, en el sistema de 0 i 1 dígits, per la qual cosa per a poder processar les dades introduïdes per nosaltres ha de passar d'una base a una altra i el mateix, però viceversa, per a presentar a l'usuari els resultats obtinguts.

El que hem volgut analitzar en aquest programa ha estat: els canvis de base.

Hem pres com a exemple les bases 10, 2 i 16, que són les que més s'utilitzen al nostre judici.

Conversió de base 10 a base n

Suposem que volem convertir a la base n un número que està en la base 10. Dividim el nombre decimal per n i guardem les restes d'aquestes divisions fins que el quocient és 0.

Ex. : Si volem convertir el nombre decimal 408 a la base 2:

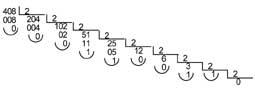
El número 408 en la base 2 serà 110011000.

Ex. : Conversió del nombre decimal 420 a la base 16

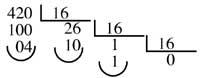
1A4 serà el número 420 en la base 16.

Nota: El sistema decimal utilitza 10 dígits i el binari 2. Per tant, l'hexadecimal haurà de tenir 16 dígits o símbols. Com només hi ha 10 xifres decimals, s'utilitzen els 6 primers caràcters de l'alfabet com a xifres.

Conversió de base n a base 10

Suposem que volem passar un número en la base n (a1 a2 ... a la base 10.

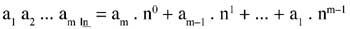
Hem de fer-ho.

No es pot fer directament per a convertir el número m-tar en n-tar sense passar per la base 10. El número m haurà de convertir-se en decimal i després en n-tar el decimal.

No obstant això, per a convertir els nombres binaris en hexadecimals tenim una ruta més senzilla que per al cas general. Per què això? Doncs perquè els quatre dígits binaris formen un número hexadecimal. Per tant, agafar els dígits binaris de dreta a esquerra, si en el grup de l'esquerra mancada xifra afegint els 0 a l'esquerra, i seguint la taula adjunta bastarà amb convertir directament a setze.

Parts del programa:

• 10-130: Presentació del menú principal i selecció d'una opció.
• 140-200: Definir el nombre d'exercicis que es volen realitzar en una sessió.
• 250-550: Resolució d'un conjunt d'exercicis.
  • 270: Un nombre decimal s'extreu aleatòriament.
  • 290-330: El nombre decimal passa a la base 2.
  • 340-400: El nombre decimal passa a la base 16.
  • 410-430: Es defineix la base en la qual han d'estar presents les preguntes o entrades i els resultats.
  • 450-530: Verificació del resultat.
• 610-640: Acció d'escriure lentament les cadenes de caràcters cap a la dreta.
• 660-690: Acció d'escriure les cadenes de caràcters cap a l'esquerra.
• 710-730: Dades del programa.

(Nota: Per a veure bé la imatge anar al pdf).