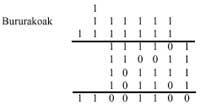
Change of base

1989/09/01 Arrojeria, Eustakio - Elhuyar Zientziaren Komunikazioa | Lizaso, Pili - Informatika SailaElhuyar Fundazioa Iturria: Elhuyar aldizkaria

• Programazioa

With the excuse that we were in the last number in summer, we offered you a game. Of course you will have played enough and at the end of the summer we have to return to the road. We are at the beginning of a new course and it is time to begin to launch the engines. We hope that the program of this number will help you in this work.

The normal system used to represent the numbers is the harmatic, that is, a system formed by ten different signs or digits (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). Anyway, you will know that the computers work in the binary system, that is, in the system of 0 and 1 digits, so to be able to process the data introduced by us it has to go from one base to another and the same, but vice versa, to present to the user the results obtained.

What we wanted to analyze in this program has been: the base changes.

We have taken as an example bases 10, 2 and 16, which are the most used in our judgment.

Conversion of base 10 to base n

Suppose we want to convert to base n a number that is in base 10. We divide the decimal number by n and keep the remains of these divisions until the quotient is 0.

Ex. : If we want to convert the decimal number 408 to the base 2:

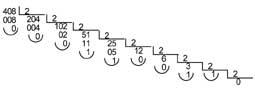
The number 408 in base 2 will be 110011000.

Ex. : Conversion of decimal number 420 to base 16

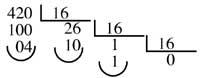
1A4 will be number 420 in base 16.

Note: Note: The decimal system uses 10 digits and binary 2. Therefore, the decimal must have 16 digits or symbols. As there are only 10 decimal numbers, the first 6 characters of the alphabet are used as figures.

Conversion of base n to base 10

Suppose we want to pass a number in base n (a1 to 2 ... to base 10.

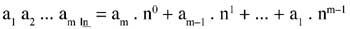
We have to do it.

It cannot be done directly to convert the number m-tar to n-tar without going through base 10. The number m must become decimal and then n-tar decimal.

However, to convert binary numbers into hexadecimal we have a simpler route than for the general case. Why this? Because the four binary digits form a hexadecimal number. Therefore, take the binary digits from right to left, if in the group of the left is missing figure adding the 0 to the left, and following the attached table will suffice to convert directly to sixteen.

Parts of the program:

• 10-130: Presentation of the main menu and selection of an option.
• 140-200: Define the number of exercises you want to perform in a session.
• 250-550: Resolution of a set of exercises.
  • 270: 270; 270; 270 A decimal number is extracted randomly.
  • 290-330: The decimal number passes to base 2.
  • 340-400: The decimal number passes to base 16.
  • 410-430: The basis on which questions or entries and results must be present is defined.
  • 450-530: Verification of the result.
• 610-640: Action to slowly write the character strings to the right.
• 660-690: Action of writing the character strings to the left.
• 710-730: Program data.

(Note: To see the image go to pdf).