Cambio de base

1989/09/01 Arrojeria, Eustakio - Elhuyar Zientziaren Komunikazioa | Lizaso, Pili - Informatika SailaElhuyar Fundazioa Iturria: Elhuyar aldizkaria

• Programazioa

Con la excusa de que estábamos en el último número en verano, os ofrecimos un juego. Por supuesto que luego habréis jugado lo suficiente y al final del verano tenemos que volver a la vía. Estamos al principio de un nuevo curso y es hora de empezar a poner en marcha los motores. Esperamos que el programa de este número os ayude en este trabajo.

El sistema normal utilizado para representar los números es el harmático, es decir, un sistema formado por diez signos o dígitos diferentes (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). De todas formas, sabréis que los ordenadores trabajan en el sistema binario, es decir, en el sistema de 0 y 1 dígitos, por lo que para poder procesar los datos introducidos por nosotros tiene que pasar de una base a otra y lo mismo, pero viceversa, para presentar al usuario los resultados obtenidos.

Lo que hemos querido analizar en este programa ha sido: los cambios de base.

Hemos tomado como ejemplo las bases 10, 2 y 16, que son las que más se utilizan a nuestro juicio.

Conversión de base 10 a base n

Supongamos que queremos convertir a la base n un número que está en la base 10. Dividimos el número decimal por n y guardamos los restos de estas divisiones hasta que el cociente es 0.

Ej. : Si queremos convertir el número decimal 408 a la base 2:

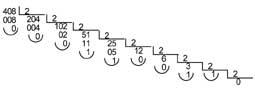
El número 408 en la base 2 será 110011000.

Ej. : Conversión del número decimal 420 a la base 16

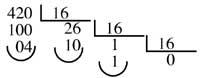
1A4 será el número 420 en la base 16.

Nota: El sistema decimal utiliza 10 dígitos y el binario 2. Por lo tanto, el hexadecimal deberá tener 16 dígitos o símbolos. Como sólo hay 10 cifras decimales, se utilizan los 6 primeros caracteres del alfabeto como cifras.

Conversión de base n a base 10

Supongamos que queremos pasar un número en la base n (a1 a2 ... a la base 10.

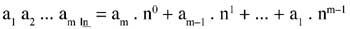
Tenemos que hacerlo.

No se puede hacer directamente para convertir el número m-tar en n-tar sin pasar por la base 10. El número m deberá convertirse en decimal y después en n-tar el decimal.

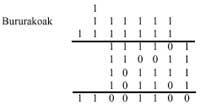
Sin embargo, para convertir los números binarios en hexadecimales tenemos una ruta más sencilla que para el caso general. ¿Por qué esto? Pues porque los cuatro dígitos binarios forman un número hexadecimal. Por lo tanto, coger los dígitos binarios de derecha a izquierda, si en el grupo de la izquierda falta cifra añadiendo los 0 a la izquierda, y siguiendo la tabla adjunta bastará con convertir directamente a dieciséis.

Partes del programa:

• 10-130: Presentación del menú principal y selección de una opción.
• 140-200: Definir el número de ejercicios que se quieren realizar en una sesión.
• 250-550: Resolución de un conjunto de ejercicios.
  • 270: Un número decimal se extrae aleatoriamente.
  • 290-330: El número decimal pasa a la base 2.
  • 340-400: El número decimal pasa a la base 16.
  • 410-430: Se define la base en la que deben estar presentes las preguntas o entradas y los resultados.
  • 450-530: Verificación del resultado.
• 610-640: Acción de escribir lentamente las cadenas de caracteres hacia la derecha.
• 660-690: Acción de escribir las cadenas de caracteres hacia la izquierda.
• 710-730: Datos del programa.

(Nota: Para ver bien la imagen ir al pdf).