Pi, endless number

2007/04/29 Rementeria Argote, Nagore - Elhuyar Zientziaren Komunikazioa

• Matematika

The number (pi) is the result of the division between the perimeter and the diameter of a circle, a constant.

Most people know the pi number; they will remind more than one of the school times. In fact, in school we learn that pi is a constant that establishes the relationship between the perimeter and the diameter of a circumference, which is the quotient between the perimeter and the diameter. Therefore, regardless of the size of the circle, the ratio between the perimeter and diameter is always the same: the constant pi.

To be able to use it in the math or physics exercises of the school you learn that pi is 3,14, 3,1416, if you want to specify more. And the truth is that for these cases it is a good approximation, but the number pi does not end, the succession of decimals is endless. There is the key to the charm of this number.

Mysterious constant

Archimedes approached much the value of pi a. C. III. Made by the painter Domenico Fetti in 1620.

Long ago men and women discovered this constant, which was very useful in architecture to make calculations. Far back in history, the Bible, for example, mentions, even indirectly, number 3. Mesopotamian mathematicians gave a value to this constant: 3 1 of 8. Archimedes came even closer to the real value of the constant, according to him, between 3 10/71 and 3 1/7. That is why he was called constant of Archimedes.

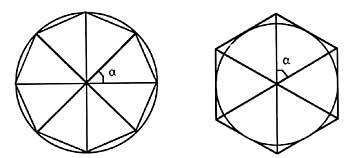
The method used by Archimedes to approach the value of the constant was based on the superposition of two polygons inside and outside a circle with the same number of sides. It made an approximation, since as the number of sides of the polygon increases, the perimeters of the two polygons are closer to the circumference perimeter. With this method, after Archimedes many mathematicians tried to approach the concrete value of the constant. More than one devoted much of his life to these calculations.

The Japanese tabaqués, for example, adding and adding the faces of the polygon of the circumference, reached a polygon of one thousand twenty-four sides, and, after this work, calculated forty-one decimals of pi. XVIII. It was in the twentieth century, in which he received the name pi of that number that caused that fascination. In 1706 he was baptized with this name by the mathematician William Jones and was spread by Leonard Euler.

Computer competence

The effort to accurately calculate the number pi has not just ended, with the most recent supercomputers calculating billions of decimals. (Photo: Lawrence Livermore National Laboratory

Over time, experienced mathematicians calculated more and more decimals. Calculators made it easier to work, and computers of course. For the first computers it was a tempting challenge to calculate decimal numbers. For example, an ENIAC computer broke all previous records in 1949: He calculated 2037 decimals in 70 hours. Since then we tried to break records with all the computers and so we have come to the current situation. The number pi we know accurately in decimal billions, but we still can't say exactly the value of nozzles. That, of course, we will never get it, it is a number that finally does not have.

Published in 7K.