Pi, número sin fin

2007/04/29 Rementeria Argote, Nagore - Elhuyar Zientziaren Komunikazioa

• Matematika

El número (pi) es el resultado de la división entre el perímetro y el diámetro de una circunferencia, una constante.

La mayoría de la gente conoce el número pi; recordará a más de uno los tiempos escolares. De hecho, en la escuela se aprende que pi es una constante que establece la relación entre el perímetro y el diámetro de una circunferencia, que es el cociente entre el perímetro y el diámetro. Por tanto, independientemente del tamaño del círculo, el cociente entre el perímetro y el diámetro es siempre el mismo: la constante pi.

Para poder utilizarlo en los ejercicios de matemáticas o física de la escuela se aprende que pi es 3,14, 3,1416, si se quiere concretar más. Y la verdad es que para estos casos es una buena aproximación, pero el número pi no tiene por fin, la sucesión de decimales es interminable. Ahí está la clave del encanto de este número.

Constante misteriosa

Arquímedes se acercó mucho al valor del pi a. C. III. Realizado por el pintor Domenico Fetti en 1620.

Hace tiempo que hombres y mujeres descubrieron esta constante, que era muy útil en arquitectura para hacer cálculos. Muy atrás en la historia, en la Biblia, por ejemplo, se menciona, aunque sea indirectamente, el número 3. Los matemáticos mesopotámicos dieron un valor a esta constante: 3 1 de 8. Arquímedes se acercó aún más al valor real de la constante, según él, entre 3 10/71 y 3 1/7. Por eso le llamaron constante de Arquímedes.

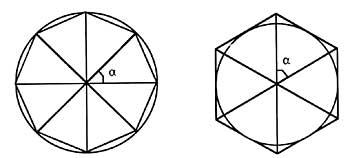
El método utilizado por Arquímedes para aproximarse al valor de la constante se basaba en la superposición de dos polígonos dentro y fuera de una circunferencia con el mismo número de lados. Hacía una aproximación, ya que a medida que el número de lados del polígono aumenta, los perímetros de los dos polígonos se aproximan más al perímetro de la circunferencia. Con este método, tras Arquímedes muchos matemáticos trataron de acercarse al valor concreto de la constante. Más de uno dedicó gran parte de su vida a estos cálculos.

El tabaqués japonés, por ejemplo, sumando y añadiendo las caras del polígono de la circunferencia, llegó a un polígono de mil veinticuatro lados, y, tras este trabajo, calculó cuarenta y un decimales del pi. XVIII. Fue en el siglo XX, en el que recibió el nombre pi de aquel número que provocaba esa fascinación. En 1706 fue bautizado con este nombre por el matemático William Jones y fue difundido por Leonard Euler.

Competencia de computadores

El esfuerzo por calcular con precisión el número pi no acaba de terminar, con los superordenadores más recientes han calculado miles de millones de decimales. (Foto: Lawrence Livermore National Laboratory )

Con el paso del tiempo, los experimentados matemáticos calcularon cada vez más decimales. Las calculadoras permitieron hacer más fácil el trabajo, y las computadoras, por supuesto. Para los primeros computadores era un reto tentador calcular los números decimales. Por ejemplo, una computadora ENIAC rompió todos los récords anteriores en 1949: Calculó 2037 decimales en 70 horas. Desde entonces se intentó romper récords con todas las computadoras y así hemos llegado a la situación actual. El número pi lo conocemos con precisión en billones decimales, pero todavía no podemos decir con exactitud el valor de las boquillas. Eso, claro, no lo vamos a conseguir nunca, es un número que finalmente no tiene.

Publicado en 7K.