Pi, numéro sans fin
2007/04/29 Rementeria Argote, Nagore - Elhuyar Zientziaren Komunikazioa

La plupart des gens connaissent le nombre pi ; il rappellera à plus d'un les temps scolaires. En fait, à l'école on apprend que pi est une constante qui établit la relation entre le périmètre et le diamètre d'une circonférence, qui est le rapport entre le périmètre et le diamètre. Par conséquent, indépendamment de la taille du cercle, le rapport entre le périmètre et le diamètre est toujours le même: la constante pi.
Pour pouvoir l'utiliser dans les exercices de mathématiques ou physique de l'école, on apprend que pi est 3,14, 3,1416, si on veut concrétiser plus. Et la vérité est que pour ces cas est une bonne approximation, mais le nombre pi n'a pas pour fin, la succession de décimales est interminable. Voici la clé du charme de ce numéro.
Constante mystérieuse

Il y a longtemps que des hommes et des femmes ont découvert cette constante, qui était très utile en architecture pour faire des calculs. Très loin dans l'histoire, dans la Bible, par exemple, on mentionne, même indirectement, le numéro 3. Les mathématiciens mésopotamiens ont donné une valeur à cette constante: 3 1 de 8. Archimède s'est approché encore plus de la valeur réelle de la constante, selon lui, entre 3 10/71 et 3 1/7. C'est pourquoi on l'appelait constant d'Archimède.
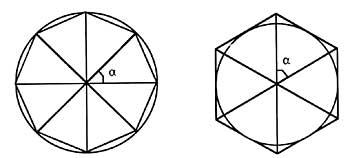
La méthode utilisée par Archimède pour approcher la valeur de la constante était basée sur la superposition de deux polygones à l'intérieur et à l'extérieur d'une circonférence avec le même nombre de côtés. Il faisait une approximation, puisque le nombre de côtés du polygone augmente, les périmètres des deux polygones s'approchent davantage du périmètre de la circonférence. Avec cette méthode, après Archimède de nombreux mathématiciens ont essayé de se rapprocher de la valeur concrète de la constante. Plus d'un a consacré une grande partie de sa vie à ces calculs.
Le tabagisme japonais, par exemple, additionnant et ajoutant les visages du polygone de circonférence, est arrivé à un polygone de mille vingt-quatre côtés, et, après ce travail, a calculé quarante et un décimales de pi. XVIII. C'est au XXe siècle qu'il reçut le nom pi de ce nombre qui provoquait cette fascination. En 1706, il a été baptisé sous ce nom par le mathématicien William Jones et a été diffusé par Leonard Euler.
Compétence informatique

L'effort pour calculer avec précision le nombre pi ne se termine pas, avec les superordinateurs les plus récents ont calculé des milliards de décimales. (Photo: Lawrence Livermore National Laboratory )
Au fil du temps, les mathématiciens expérimentés ont calculé de plus en plus décimales. Les calculatrices ont permis de faciliter le travail, et les ordinateurs, naturellement. Pour les premiers ordinateurs était un défi tentant de calculer les nombres décimaux. Par exemple, un ordinateur ENIAC a cassé tous les records précédents en 1949 : Il a calculé 2037 décimales en 70 heures. Depuis lors, nous avons essayé de briser des records avec tous les ordinateurs et ainsi nous sommes arrivés à la situation actuelle. Le nombre pi est connu avec précision en milliards décimaux, mais nous ne pouvons pas encore dire avec exactitude la valeur des buses. Cela, bien sûr, nous ne l'obtiendrons jamais, c'est un nombre qui n'a finalement pas.
Publié dans 7K.

Gai honi buruzko eduki gehiago
Elhuyarrek garatutako teknologia