Pi, número sen fin
2007/04/29 Rementeria Argote, Nagore - Elhuyar Zientziaren Komunikazioa

A maioría da xente coñece o número pi; lembrará a máis dun os tempos escolares. De feito, na escola apréndese que pi é una constante que establece a relación entre o perímetro e o diámetro dunha circunferencia, que é o cociente entre o perímetro e o diámetro. Por tanto, independentemente do tamaño do círculo, o cociente entre o perímetro e o diámetro é sempre o mesmo: a constante pi.
Paira poder utilizalo nos exercicios de matemáticas ou física da escola apréndese que pi é 3,14, 3,1416, se se quere concretar máis. E a verdade é que paira estes casos é una boa aproximación, pero o número pi non ten por fin, a sucesión de decimais é interminable. Aí está a clave do encanto deste número.
Constante misteriosa

Hai tempo que homes e mulleres descubriron esta constante, que era moi útil en arquitectura paira facer cálculos. Moi atrás na historia, na Biblia, por exemplo, menciónase, aínda que sexa indirectamente, o número 3. Os matemáticos mesopotámicos deron un valor a esta constante: 3 1 de 8. Arquímedes achegouse aínda máis ao valor real da constante, segundo el, entre 3 10/71 e 3 1/7. Por iso chamáronlle constante de Arquímedes.
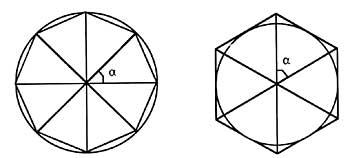
O método utilizado por Arquímedes paira aproximarse ao valor da constante baseábase na superposición de dous polígonos dentro e fóra dunha circunferencia co mesmo número de lados. Facía una aproximación, xa que a medida que o número de lados do polígono aumenta, os perímetros dos dous polígonos aproxímanse máis ao perímetro da circunferencia. Con este método, tras Arquímedes moitos matemáticos trataron de achegarse ao valor concreto da constante. Máis dun dedicou gran parte da súa vida a estes cálculos.
O tabaqués xaponés, por exemplo, sumando e engadindo as caras do polígono da circunferencia, chegou a un polígono de mil vinte e catro lados, e, tras este traballo, calculou corenta e un decimais do pi. XVIII. Foi no século XX, no que recibiu o nome pi daquel número que provocaba esa fascinación. En 1706 foi bautizado con este nome polo matemático William Jones e foi difundido por Leonard Euler.
Competencia de computadores

O esforzo por calcular con precisión o número pi non acaba de terminar, cos supercomputadores máis recentes calcularon miles de millóns de decimais. (Foto: Lawrence Livermore National Laboratory )
Co paso do tempo, os experimentados matemáticos calcularon cada vez máis decimais. As calculadoras permitiron facer máis fácil o traballo, e as computadoras, por suposto. Paira os primeiros computadores era un reto tentador calcular os números decimais. Por exemplo, una computadora ENIAC rompeu todas as marcas anteriores en 1949: Calculou 2037 decimais en 70 horas. Desde entón tentouse romper marcas con todas as computadoras e así chegamos á situación actual. O número pi coñecémolo con precisión en billóns decimais, pero aínda non podemos dicir con exactitude o valor das boquillas. Iso, claro, non o imos a conseguir nunca, é un número que finalmente non ten.
Publicado en 7K.

Gai honi buruzko eduki gehiago
Elhuyarrek garatutako teknologia