Pintxo-pote kontuak, blockchain a eta bitcoin a

2018/09/17 Ander Galisteo Zabalo - IMDEA Networks Institutua (Madril); Carlos III Unibertsitatea (Madril) Iturria: Elhuyar aldizkaria

• Programazioa
• Internet

Os beneficios de Internet son innegables. Por primeira vez dispomos dunha ferramenta que conecta a toda a sociedade. Con todo, esta conexión creou unha novo paradigma. Os usuarios non podemos saber si a persoa que está alén da rede é fiable. Por tanto, como podemos conseguir que todos compartamos información sen que ninguén substitúa a identidade de ninguén e cambie a información privada?

Neste artigo analizarase a solución máis coñecida que se atopou nos últimos anos paira solucionar este problema, tomando como exemplo a realización de contas con amigos como o blockchain ou as cadeas de bloques[3][6]. Paira iso, en primeiro lugar, exporanse una serie de conceptos imprescindibles paira entender que son as cadeas de bloques, así como os beneficios e problemas que poden supor.

Que son as cadeas de bloques?

Imaxinemos que estamos con amigos, por exemplo, no bote de pintxos do barrio donostiarra de Gros. Como pagamos os nosos botes de pintxos? Por unha banda, é posible que cada un pague o seu, pero está claro que non é a opción máis eficiente, xa que nos custaría moito tempo pagar. Outra opción sería pór un bote entre todos, porque así pagariamos moito máis rápido. Con todo, isto expón outros problemas: que pasaría si o diñeiro da lata non fose suficiente? E si está a sobrar ao final? Moitas veces non todos os prezos son iguais, neste caso, como distribuiriamos o prezo?

Á vista destes problemas podemos pensar nunha solución máis adecuada. Imos crear una conta na que cada un dos membros poña en cada bar canto debe e a quen debe. Para que esta conta sexa o máis transparente posible, en lugar de estar escrita nun papel, todos os datos estarán online para que todos poidan velos, por exemplo, nun grupo de WhatsApp. Pero que pasaría si os membros do equipo non fosen fiables? Vexamos que trucos podemos utilizar paira solucionar este problema de fiabilidade. Á fin e ao cabo, a cadea de bloques é só esa, una conta enorme que todo participante pode utilizar paira escribir transaccións entre eles. Vexamos, por tanto, que é una transacción.

Transacción

Como xa se indicou, aparecerá na conta canto e a quen debe cada persoa en cada bar. Hai dúas formas de facelo: que quen paga anóteo na conta ou quen o debe escríbeo. Está claro que a primeira opción non é conveniente, xa que se algún participante faltase diñeiro poderíase pór en conta que outros lle deben. Por tanto, será o debedor quen anote o importe e a quen debe. Así, aseguraremos que ninguén fará trampas porque ao escribir algo na conta pérdese diñeiro. Isto denomínase transacción nas cadeas de bloques. Pero como podemos saber se realmente é capaz de pagar o importe que escribiu? Moi fácil. Cada vez que se escribe una transacción, cada persoa que se atope nesa conta (neste caso no grupo WhatsApp) debe comprobar se o debedor ten a moeda suficiente paira pagar a transacción. Se non é así, cancélase a transacción. E como podemos saber si ten suficiente? Sinxelamente, porque observando todas as transaccións anteriores podemos saber si ten suficiente paira saldar a débeda. Neste punto xa podemos detectar onde está o valor da conta (no noso caso o grupo WhatsApp): podemos utilizar nun novo bote de pintxos o importe que me deberon previamente. De todos os xeitos, como podemos asegurar que só escribo as miñas transaccións?

Firma dixital

Firma dixital[1] xorde paira solucionar un único problema: verificar a orixe dunha mensaxe. Aínda que os seres humanos vexamos unha mensaxe como un conxunto de letras, un computador ve unha mensaxe como un conxunto de bits (calquera arquivo, en verdade).

Supoñamos que temos moitos usuarios. Os algoritmos de creación de firma dixital son dúas: o primeiro utilízase paira crear a firma e o segundo paira verificar a firma. Cada usuario ten dous códigos chamados chave, uno privado (Iphone) e outro público (Gpu). A función de creación de firma é:

asina = firma (mensaxe Iphone)

Figura : Leire espera unha mensaxe de Xabi. Nagore quere enviar unha mensaxe a Leire en nome de Xabi paira enganar a Leire. Con todo, Xabi asinou a mensaxe coa súa chave privada. Leire comproba entón con firma pública as dúas firmas recibidas e identifica a de Xabi e rexeita a de Nagore. Ed. Ander Galisteo

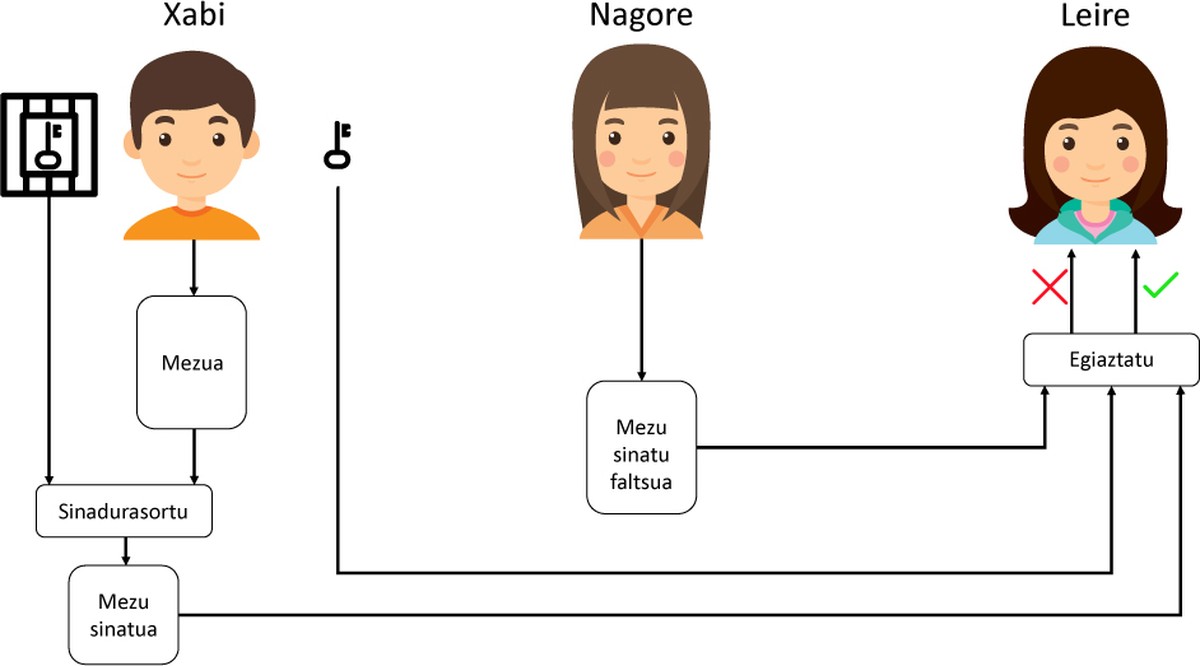
Aquí percibimos a diferenza máis significativa entre a firma das persoas e a firma dixital. Como pode verse, cada firma créase paira cada mensaxe e usuario, polo que a firma dixital dependerá da mensaxe e do usuario (as persoas utilizamos a mesma asina paira asinar todos os documentos). Isto significa, entre outras cousas, que podemos utilizar noso GPRS en diferentes mensaxes sen perder seguridade.

Doutra banda, temos outra función de verificación de firma:

se/non = comprobar(mensaxe, Gpu, firma)

Esta función indícanos a orixe da firma utilizando a firma, a mensaxe e a chave pública. Desta forma sinxela podemos saber se a mensaxe foi enviado polo usuario que realmente queremos. A modo de exemplo, ver figura 1.

Bloque

O que dixemos até agora sería útil nunha cuadrilla pequena, e poderíase aplicar sen problemas. Pero normalmente no poteo de pintxos non adoitamos estar coa cuadrilla, normalmente atopámonos cos do equipo deportivo, da universidade, dos membros do grupo de baile... e neste caso non nos serve o que fixemos coa cuadrilla. Fagamos entón o grupo WhatsApp de San Sebastián, un grupo que englobe a todos os donostiarras. E hai alguén de Vitoria? Fagamos entón o equipo de Euskadi. E hai alguén máis? Ben, fagamos un equipo mundial. Pero agora xórdenos un gran problema. Nun grupo de WhatsApp a nivel mundial, está claro que non seremos capaces de ler todas as mensaxes e aínda será máis difícil comprobar todas as transaccións (mensaxes): non saberemos a quen debe, nin en que orde realizáronse as transaccións (non é o mesmo gastar despois de recibir o diñeiro que gastar primeiro o diñeiro e despois recibir o diñeiro, que non é legal). Por iso, nunha gran conta é imprescindible unir as transaccións nunha cantidade fixa creando bloques[5]. Por tanto, cada mensaxe de WhatsApp será un conxunto de transaccións.

Con todo, podemos pensar que isto non soluciona o problema, xa que agora en lugar dunha chea de transaccións temos unha chea de bloques. Se cada usuario crea un bloque non solucionaremos o problema. Por iso, debe ser difícil crear un bloque paira un usuario, pero sinxelo paira outros usuarios saber se o bloque está ben creado. Como podemos facelo?

Funcións Hash

As funcións Hash[4] son funcións moi útiles paira converter un conxunto de datos en datos de tamaño coñecido.

hash = hashfunción (mensaxe)

Figura : Algúns exemplos da función Hash[2]. Como se pode observar nos exemplos 1, 2 e 3, cando o cambio é moi pequeno prodúcese un hash moi diferente. Doutra banda, hai que ter en conta que ten igual a lonxitude da mensaxe (no cuarto exemplo, Maritxu nora joan utilizouse toda a canción paira crear o hash), xa que a lonxitude do hash sempre será do mesmo tamaño.

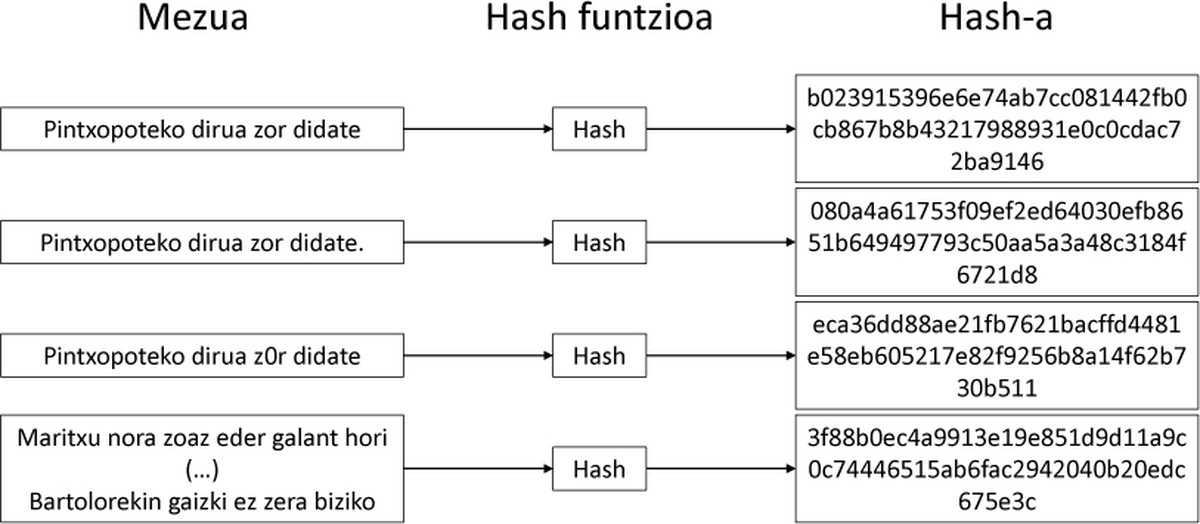
Con todo, as funcións Hash teñen una propiedade moi especial: se cambiamos un pouco a mensaxe, a saída variará moito. O cambio é tan grande que nos parece aleatorio a saída de dúas mensaxes moi similares. Na figura 2 móstrase un exemplo claro.

Por tanto, si a nós dannos unha mensaxe, é moi fácil conseguir a súa hash, pero co hash non poderemos saber cal era a mensaxe orixinal. A única maneira de conseguilo é a través de ensaios, cambiando a mensaxe até conseguir o hash desexado.

E como nos pode axudar? Un bloque (un conxunto de transaccións) é só unha mensaxe. Así, podemos atopar o hash do bloque, tendo sempre en conta que o hash do noso bloque variará en función do contido e orde das transaccións.

Agora imos escribir algo ao final do bloque, un conxunto de caracteres. Pero, por que?

Proof-of-work

Vaise a pór una restrición aos bloques: o hash do bloque ten que ter varios 0 ao principio. Paira conseguilo, tal e como se indicou anteriormente, ao final do bloque escribiremos un conxunto de caracteres chamado número máxico. Como dixemos, non é posible volver do hash á mensaxe, xa que a única forma de obter os 0 é tentar moitas combinacións de caracteres até conseguir a cantidade 0 desexada. Este cálculo consome moitos recursos do computador (tempo e electricidade). Isto quere dicir que se un bloque ten un hash de moitos 0, alguén gastou moita enerxía en calculala, polo que é un bloque fiable.

Figura : Os bloques divídense en tres partes. A primeira é o hash do bloque anterior, de forma que todos os bloques están en orde. A segunda é a transacción do bloque. O último é un número máxico que se utiliza paira empezar o hash con 0. Ed. Ander Galisteo

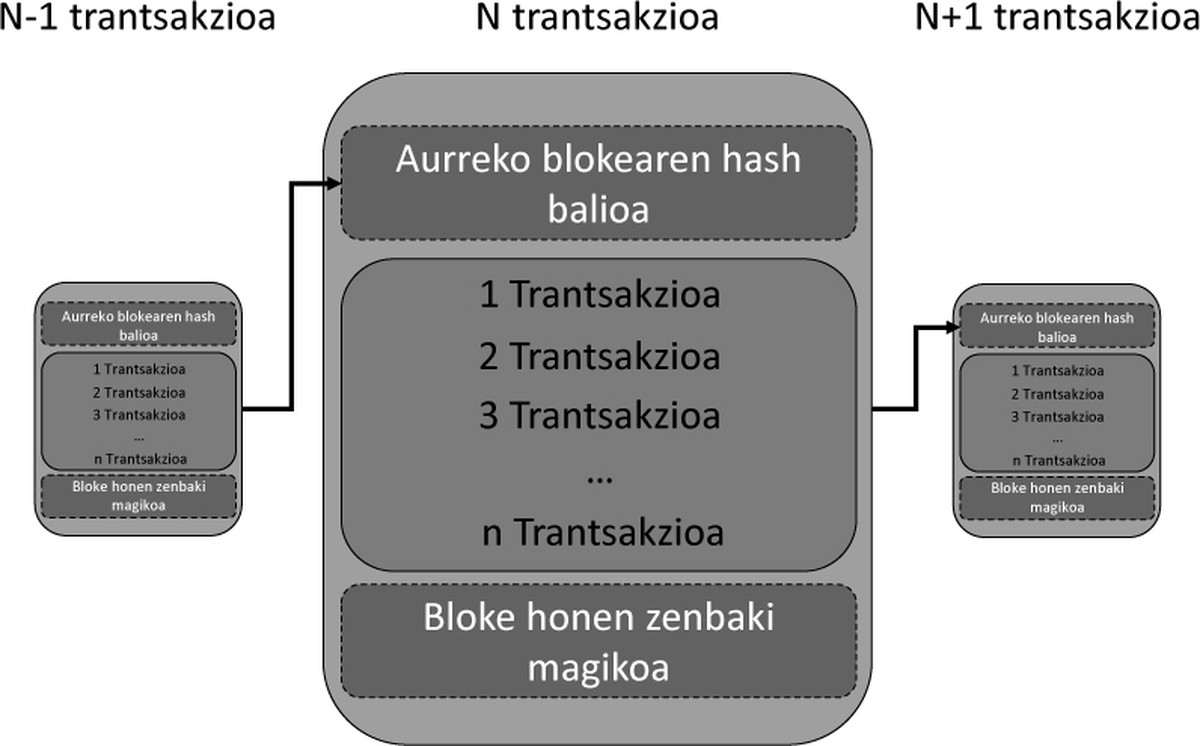
Como dixemos, é fácil comprobar se se cumpre a regra do hash. Por iso, non ten sentido tentar facer trampas, xa que lles atraparían con facilidade. Pero, por que a xente faríao? Por que facer todos estes cálculos paira calcular o hash do bloque? A resposta é sinxela, porque hai un premio paira quen primeiro crea o bloque. Este premio non é máis que un valor dentro da conta: no exemplo da cuadrilla a comida ou bebida paira o poteo de pintxos, no caso da vitcoina as bitcoinas. Este proceso denomínase minería. O bloque complétase co hash do bloque anterior. Así os bloques están ordenados. Na figura 3 móstrase a estrutura do bloque.

Relación entre cadeas de bloques e bitcoina

Pero, entón, como se relacionan a estrutura que describimos (cadeas de bloques) coa criptomoneta máis famosa do mundo? O das cadeas de bloques é só un concepto, una forma de levar contas. Moeda das cadeas de bloques Bitcoina, moeda electrónica paira levar contas utilizando cadeas de bloques. Da mesma maneira, a suma é só un concepto matemático e una expresión de "5+2".

Conclusións

Aínda que máis descoñecida, neste artigo atribuíuse ás cadeas de bloques unha énfase maior que á vitcoina. Por que? Pois porque ademais da vitcoina hai moitas outras criptomonetas (ethereum, litecoin, dash..), pero todas son expresións do mesmo concepto: das cadeas de bloques. As criptomonetas poden subir ou baixar no mercado, poden crearse e desaparecer. En calquera caso, está claro que as cadeas de bloques estarán presentes na nosa vida nos próximos anos nas criptomonetas paira compartir información ou, quizais, paira evitar problemas de pintxo-poteo.

Referencias

[1] Whitfield Diffie and Martin Hellman. New directions in cryptography. En: IEEE transactions on Information Theory 22.6 (1976), pp. 644–654.

[2] FileFormat.info: Hash functions. https :// www . fileformat . info / tool/hash.htm

[3] Satoshi Nakamoto. Bitcoin: A Peer-to-Peer Electronic Cash System. Novembro 2008. 2015

[4] Bart Preneel. “The first 30 years of cryptographic hash functions and the NIST XA-3 competition”. En: Cryptographers’ track at the RSA conference. Springer. 2010, pp. 1–14.

[5] Melanie Swan. Blockchain: Blueprint for a new economy. "Ou’Reilly Me- dia, Inc.", 2015

[6] Youtube channel 3Blue1Brown: Ever wonder how Bitcoin (and other cryptocurrencies) actually work? https://www.youtube.com/watch? v=bbc-nXj3Ng4.