Poliminos (I)
1990/01/01 Angulo, Patxi Iturria: Elhuyar aldizkaria
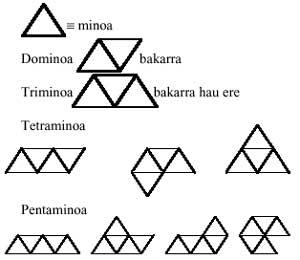
Es tracta d'un popular joc de 28 peces va dominar. La paraula dominó prové del Llatí i significa Jaun. No obstant això, nosaltres inventarem un altre origen: Domino = dos minos. És a dir, Dominó podria significar dos minos. Mirant les peces del joc, descobriràs que totes estan formades per dos quadres. Per tant, seguint la nostra hipòtesi, la paraula mino correspondria a la paraula quadrat.
Aquesta serà l'excusa per a construir altres poliminos des del dominó. A partir d'ara ens oblidarem del joc dominical i ens ocuparem de la seva estructura, sempre sota la hipòtesi que "mino = quadrat".

Afegint dos minos s'obté una peça. La peça sembla ser única encara que s'afegeixin de qualsevol manera. A aquesta peça li direm dominó i en ser única en forma no dóna molt joc.
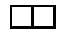
Abans de seguir endavant, t'avisem que les peces obtingudes a través de totes les simetries (en el pla) i girs (en el pla i en l'espai) possibles són iguals. Posteriorment li posarem un exemple perquè ho entengui fàcilment.
Abordem la construcció de triminos. Per a això afegim un mino més al dominó, obtenint dos triminos diferents:

Els triminos tampoc ens donen molt joc. No obstant això, amb aquestes dues peces es poden realitzar diverses figures, com es veu a continuació:
No obstant això, no és possible realitzar un rectangle de 2x3, com es pot comprovar fàcilment.
Podem passar, per tant, a la següent, els tetraminos. Per a la formació dels tetraminos, retindrem el trimino de totes maneres:
Restant els mateixos s'obtenen cinc tetraminos diferents:

Els cinc tetraminos recullen un total de 20 minos. Amb elles es poden realitzar rectangles de 2x10 i 4x5. No obstant això, cap dels cinc tetraminos pot completar-se. Per contra, si amb cinc peces es poden realitzar les següents imatges:
Avanzemos formant pentaminos. De nou reprenem els tetraminos amb un mino, de totes maneres:
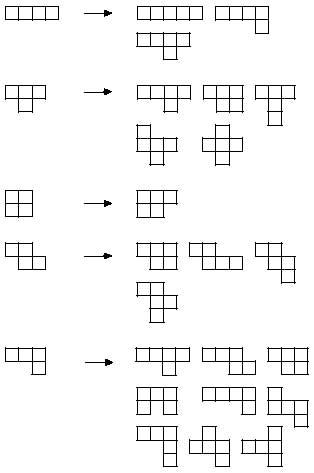
Seleccionant només diferents, s'obté 12 pentaminos:

Vegem ara l'exemple inicialment promès:
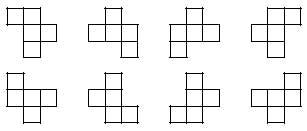
Considerem totes les peces que apareixen en la imatge com a iguals.
Amb 12 pentaminos es recullen 60 minos que permeten realitzar rectangles de 2x30, 3x20, 4x15, 5x12 i 6x10. És clar que el primer no es pot completar amb 2x30 pentaminos, ja que la meitat de les peces necessita 3 amples en totes dues direccions. Hem trobat una solució de rectangle 3x20 i no creiem que sigui l'única.

També tenim una altra solució per a la mesura 4x15. Per a 5x12 no s'ha trobat cap solució. La nostra sessió no ha estat completa. Per tant, no podem dir que no tingui solució. Si Vostè trobés algun, li agrairíem que ens ho enviés.
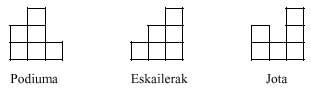
Tenim més informació sobre el rectangle de dimensió 6x10 i podem afirmar que hi ha solució i que no és l'única; que a més de les simètriques té moltes solucions (més de 1.000), com apareix en la presentació d'una marca que produeix el joc de pentamino.
A més dels rectangles existeixen altres figures que poden formar pentaminos. Imatges com:
A partir dels pentaminos s'obtenen 119 hexaminos, dels quals només 35 són diferents. Si ja és difícil utilitzar els 12 pentaminos, pensa en 35 examinos manejant. De totes maneres, si ets valent, aquí tens 35 hexaminos diferents:

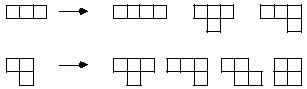
Tenint en compte que en els 35 hexaminos hi ha 210 minos, es poden formar rectangles de dimensions 2x105, 3x70, 5x42, 6x35, 7x30, 10x21 i 14x15. Igual que en els casos anteriors, la primera no es pot completar amb hexaminos. No sabem si es poden formar o no uns altres. Aquí tens el treball si tens curiositat. En els hexaminos de la imatge, quins són els que es poden aconseguir plegant la galleda de la tridimensión?
Hi ha altres opcions per a jugar amb els poliminos. Una vegada més hem de fugir dels dominis, triminos i tetraminos, que ens ofereixen poques possibilitats. Per contra, els pentaminos i els examinats són adequats en nombre de peces per al següent joc.
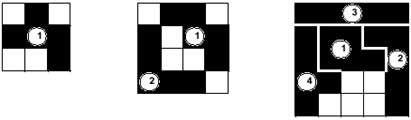
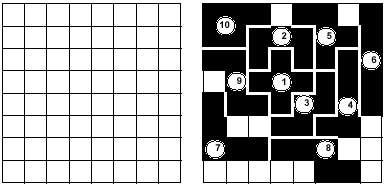
Encara que el joc admet moltes modalitats, en el fons no canvia. Els jugadors (dos, tres, quatre,...) col·locaran les peces en la taula per torns. Guanyarà qui posi l'últim pentamino. En l'exemple de la imatge, el segon jugador ha guanyat el partit, ja que ha col·locat l'últim pentamino (10). Els 12 pentaminos podrien repartir-se aleatòriament entre els jugadors, o bé una altra possibilitat és que els jugadors puguin triar les peces del mateix munt. També es pot jugar per parelles de dues maneres.
També es podrien modificar les dimensions del tauler. La talla més petita és 3x3, ja que algunes peces així ho requereixen. En la taula 3x3 el joc no té fons, ja que el primer jugador sempre gana, ja que en ella només s'inclou un pentamino. En la taula 4x4, per contra, sempre guanyarà el segon jugador. Amb això volem dir que encara que el primer jugador triï la peça que desitgi, el segon sempre tindrà l'opció de col·locar l'última peça. A més, en tots els altres casos l'elecció del segon jugador no serà única. Et deixem que inventis aquest cas especial (el cas del jugador 2 té una única oportunitat).

En la taula 5x5 sempre guanyarà el primer jugador si seleccionem bé la primera peça. Quina és aquesta peça?
A partir d'ara les possibilitats es multipliquen en taules de major dimensió i és difícil realitzar una anàlisi detallada. D'altra banda, el tauler no té quadrilàter i es podrien triar altres grandàries com els rectangles 5x6, 3x20, 4x15, 5x12 o 6x10. En la taula 5x6 hi ha una jugada adequada perquè el primer jugador sempre guanyi. Quin és?
Es pot fer el mateix per a jugar amb els hexaminos. L'estudi per a aquest cas es convertiria en inacabable, ja que hi ha 35 peces. A més, ofereix més possibilitats quant al nombre de peces. Aquí està el rectangle de 14x15 per a jugar amb els hexaminos.

Gai honi buruzko eduki gehiago
Elhuyarrek garatutako teknologia