Poliminos (I)
1990/01/01 Angulo, Patxi Iturria: Elhuyar aldizkaria
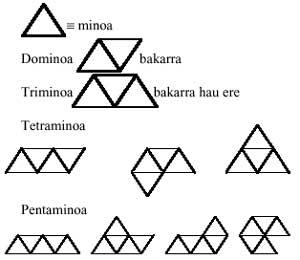
Se trata de un popular juego de 28 piezas dominó. La palabra dominó proviene del Latín y significa Jaun. Sin embargo, nosotros inventaremos otro origen: Domino = dos minos. Es decir, Dominó podría significar dos minos. Mirando las piezas del juego, descubrirás que todas están formadas por dos cuadros. Por lo tanto, siguiendo nuestra hipótesis, la palabra mino correspondería a la palabra cuadrado.
Esta será la excusa para construir otros poliminos desde el dominó. A partir de ahora nos olvidaremos del juego dominical y nos ocuparemos de su estructura, siempre bajo la hipótesis de que "mino = cuadrado".

Añadiendo dos minos se obtiene una pieza. La pieza parece ser única aunque se añadan de cualquier manera. A esta pieza le llamaremos dominó y al ser única en forma no da mucho juego.
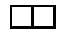
Antes de seguir adelante, te avisamos de que las piezas obtenidas a través de todas las simetrías (en el plano) y giros (en el plano y en el espacio) posibles son iguales. Posteriormente le pondremos un ejemplo para que lo entienda fácilmente.
Abordemos la construcción de triminos. Para ello añadimos un mino más al dominó, obteniendo dos triminos diferentes:

Los triminos tampoco nos dan mucho juego. Sin embargo, con estas dos piezas se pueden realizar varias figuras, como se ve a continuación:
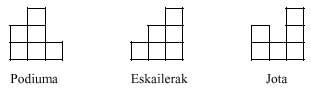
Sin embargo, no es posible realizar un rectángulo de 2x3, como se puede comprobar fácilmente.
Podemos pasar, por tanto, a la siguiente, los tetraminos. Para la formación de los tetraminos, vamos a retener el trimino de todas formas:
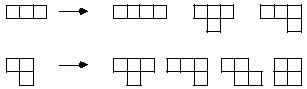
Restando los mismos se obtienen cinco tetraminos diferentes:

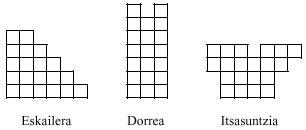
Los cinco tetraminos recogen un total de 20 minos. Con ellas se pueden realizar rectángulos de 2x10 y 4x5. Sin embargo, ninguno de los cinco tetraminos puede completarse. Por el contrario, si con cinco piezas se pueden realizar las siguientes imágenes:
Avanzemos formando pentaminos. De nuevo retomamos los tetraminos con un mino, de todas formas:
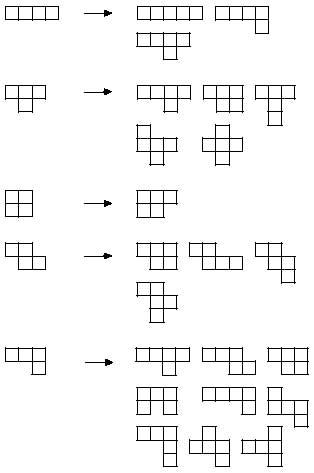
Seleccionando sólo diferentes, se obtiene 12 pentaminos:

Veamos ahora el ejemplo inicialmente prometido:
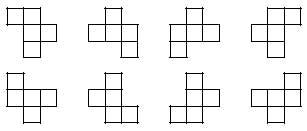
Consideramos todas las piezas que aparecen en la imagen como iguales.
Con 12 pentaminos se recogen 60 minos que permiten realizar rectángulos de 2x30, 3x20, 4x15, 5x12 y 6x10. Está claro que el primero no se puede completar con 2x30 pentaminos, ya que la mitad de las piezas necesita 3 anchas en ambas direcciones. Hemos encontrado una solución de rectángulo 3x20 y no creemos que sea la única.

También tenemos otra solución para la medida 4x15. Para 5x12 no se ha encontrado ninguna solución. Nuestra sesión no ha sido completa. Por lo tanto, no podemos decir que no tenga solución. Si Vd. encontrase alguno, le agradeceríamos que nos lo enviara.
Tenemos más información sobre el rectángulo de dimensión 6x10 y podemos afirmar que hay solución y que no es la única; que además de las simétricas tiene muchas soluciones (más de 1.000), como aparece en la presentación de una marca que produce el juego de pentamino.
Además de los rectángulos existen otras figuras que pueden formar pentaminos. Imágenes como:
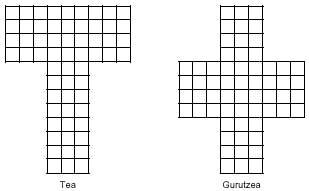
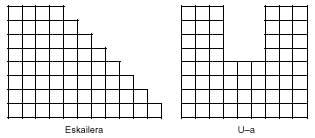
A partir de los pentaminos se obtienen 119 hexaminos, de los que sólo 35 son diferentes. Si ya es difícil utilizar los 12 pentaminos, piensa en 35 examinos manejando. De todas formas, si eres valiente, aquí tienes 35 hexaminos diferentes:

Teniendo en cuenta que en los 35 hexaminos hay 210 minos, se pueden formar rectángulos de dimensiones 2x105, 3x70, 5x42, 6x35, 7x30, 10x21 y 14x15. Al igual que en los casos anteriores, la primera no se puede completar con hexaminos. No sabemos si se pueden formar o no otros. Ahí tienes el trabajo si tienes curiosidad. En los hexaminos de la imagen, ¿cuáles son los que se pueden conseguir plegando el cubo de la tridimensión?
Hay otras opciones para jugar con los poliminos. Una vez más tenemos que huir de los dominios, triminos y tetraminos, que nos ofrecen pocas posibilidades. Por el contrario, los pentaminos y los examinados son adecuados en número de piezas para el siguiente juego.
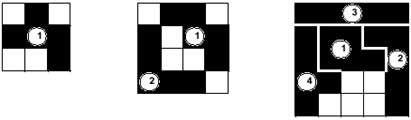
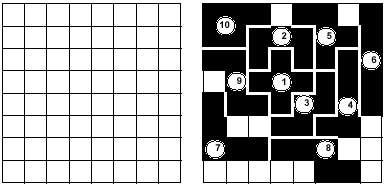
Aunque el juego admite muchas modalidades, en el fondo no cambia. Los jugadores (dos, tres, cuatro,...) colocarán las piezas en la tabla por turnos. Ganará quien ponga el último pentamino. En el ejemplo de la imagen, el segundo jugador ha ganado el partido, ya que ha colocado el último pentamino (10). Los 12 pentaminos podrían repartirse aleatoriamente entre los jugadores, o bien otra posibilidad es que los jugadores puedan elegir las piezas del mismo montón. También se puede jugar por parejas de dos maneras.
También se podrían modificar las dimensiones del tablero. La talla más pequeña es 3x3, ya que algunas piezas así lo requieren. En la tabla 3x3 el juego no tiene fondo, ya que el primer jugador siempre gana, ya que en ella sólo se incluye un pentamino. En la tabla 4x4, por el contrario, siempre ganará el segundo jugador. Con esto queremos decir que aunque el primer jugador elija la pieza que desee, el segundo siempre tendrá la opción de colocar la última pieza. Además, en todos los demás casos la elección del segundo jugador no será única. Te dejamos que inventes este caso especial (el caso del jugador 2 tiene una única oportunidad).

En la tabla 5x5 siempre ganará el primer jugador si seleccionamos bien la primera pieza. ¿Cuál es esa pieza?
A partir de ahora las posibilidades se multiplican en tablas de mayor dimensión y es difícil realizar un análisis detallado. Por otra parte, el tablero no tiene cuadrilátero y se podrían elegir otros tamaños como los rectángulos 5x6, 3x20, 4x15, 5x12 o 6x10. En la tabla 5x6 hay una jugada adecuada para que el primer jugador siempre gane. ¿Cuál es?
Se puede hacer lo mismo para jugar con los hexaminos. El estudio para este caso se convertiría en inacabable, ya que hay 35 piezas. Además, ofrece más posibilidades en cuanto al número de piezas. Ahí está el rectángulo de 14x15 para jugar con los hexaminos.

Gai honi buruzko eduki gehiago
Elhuyarrek garatutako teknologia