Polymènes (I)

1990/01/01 Angulo, Patxi Iturria: Elhuyar aldizkaria

• Matematika

Le mot omino vient du Dominus latin et signifie Jaun. Cependant, nous inventerons une autre origine: Domino = deux minos.

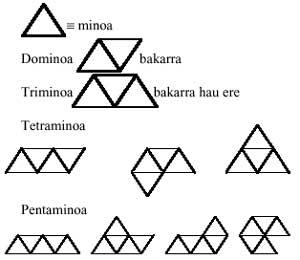
Il s'agit d'un jeu populaire de 28 pièces domino. Le mot domino vient du latin et signifie Jaun. Cependant, nous inventerons une autre origine: Domino = deux minos. En d'autres termes, Domino pourrait signifier deux minos. En regardant les pièces du jeu, vous découvrirez qu'elles sont toutes composées de deux tableaux. Par conséquent, suivant notre hypothèse, le mot mino correspondrait au mot carré.

Ce sera l'excuse pour construire d'autres polymines depuis le domino. A partir de maintenant nous oublierons le jeu dominical et nous nous occuperons de sa structure, toujours sous l'hypothèse que "mino = carré".

En ajoutant deux minos vous obtenez une pièce. La pièce semble être unique même si elle est ajoutée de toute façon. Cette pièce sera appelée domino et être unique en forme ne donne pas beaucoup de jeu.

Avant d'aller de l'avant, nous vous informons que les pièces obtenues à travers toutes les symétries (dans le plan) et les tours (dans le plan et dans l'espace) possibles sont identiques. Par la suite, nous allons vous donner un exemple pour le comprendre facilement.

Nous abordons la construction de trimins. Pour cela, nous ajoutons un mino de plus au domino, obtenant deux trimins différents:

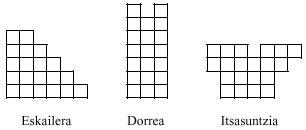
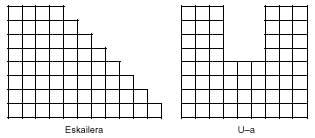
Les trimins ne nous donnent pas non plus beaucoup de jeu. Cependant, avec ces deux pièces, vous pouvez effectuer plusieurs figures, comme ci-dessous:

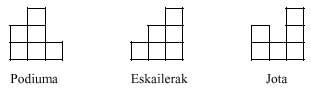
Cependant, il n'est pas possible de réaliser un rectangle de 2x3, comme vous pouvez le vérifier facilement.

Nous pouvons donc passer à la suivante, les tétramins. Pour la formation des tétramins, nous allons retenir le trimino de toute façon:

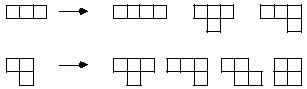
En soustrayant les mêmes, on obtient cinq tétramins différents:

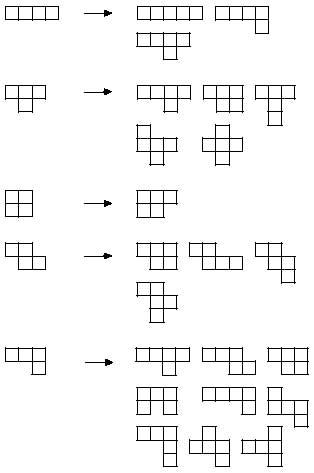
Les cinq tétramins recueillent un total de 20 minos. Avec elles on peut réaliser des rectangles de 2x10 et 4x5. Cependant, aucun des cinq tétramins ne peut être complété. Au contraire, si avec cinq pièces vous pouvez faire les images suivantes:

Avançons en formant des pentaminos. Nous reprenons de nouveau les tétramins avec un mino, de toute façon:

En sélectionnant seulement différents, vous obtenez 12 portées:

Voyons maintenant l'exemple initialement promis:

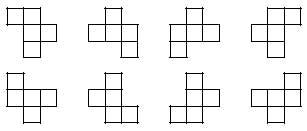
Nous considérons toutes les pièces qui apparaissent sur l'image comme égales.

Avec 12 pentaminos sont recueillies 60 minos qui permettent de réaliser des rectangles de 2x30, 3x20, 4x15, 5x12 et 6x10. Il est clair que le premier ne peut pas être complété avec 2x30 portées, puisque la moitié des pièces a besoin de 3 larges dans les deux sens. Nous avons trouvé une solution de rectangle 3x20 et nous ne pensons pas qu'elle soit la seule.

Nous avons également une autre solution pour la mesure 4x15. Aucune solution n'a été trouvée pour 5x12. Notre session n'a pas été complète. Par conséquent, nous ne pouvons pas dire que vous n'avez pas de solution. Oui Vous. trouver quelqu'un, nous vous serions reconnaissants de nous l'envoyer.

Nous avons plus d'informations sur le rectangle de dimension 6x10 et nous pouvons affirmer qu'il y a solution et que ce n'est pas la seule; qu'en plus des symétriques il a beaucoup de solutions (plus de 1.000), comme il apparaît dans la présentation d'une marque qui produit le jeu de pentamino.

En plus des rectangles, il existe d'autres figures qui peuvent former des portées. Des images comme:

A partir des pentaminos on obtient 119 hexamines, dont seulement 35 sont différents. S'il est déjà difficile d'utiliser les 12 pentaminos, pensez à 35 examines en manipulant. Cependant, si vous êtes courageux, voici 35 hexamins différents :

Étant donné que les 35 hexamines comptent 210 minos, on peut former des rectangles de dimensions 2x105, 3x70, 5x42, 6x35, 7x30, 10x21 et 14x15. Comme dans les cas ci-dessus, le premier ne peut pas être complété par des hexamines. Nous ne savons pas si d'autres peuvent être formés ou non. Voici le travail si vous êtes curieux. Dans les hexamins de l'image, quels sont ceux qui peuvent être obtenus en pliant le cube de la tridimension?

Il existe d'autres options pour jouer avec les polymines. Encore une fois, nous devons fuir les domaines, triminos et tétramins, qui nous offrent peu de possibilités. En revanche, les portées et les examinés sont adaptés en nombre de pièces pour le prochain jeu.

Pour jouer avec les pentaminos nous utiliserons un tableau de 8x8 carrés (d´échecs) et les mesures des carrés seront celles du mino.

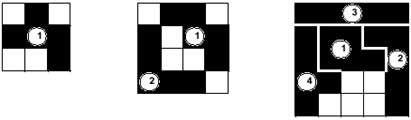
Bien que le jeu supporte de nombreuses modalités, il ne change pas en arrière-plan. Les joueurs (deux, trois, quatre,...) placeront les pièces sur la table par tour. Celui qui pose la dernière portée gagnera. Dans l'exemple de l'image, le deuxième joueur a gagné le match car il a placé la dernière portée (10). Les 12 pentaminos peuvent être distribués aléatoirement entre les joueurs, ou une autre possibilité est que les joueurs puissent choisir les pièces du même groupe. Vous pouvez également jouer par paires de deux façons.

Vous pouvez également modifier les dimensions du tableau. La taille la plus petite est 3x3, car certaines pièces le nécessitent. Dans le tableau 3x3 le jeu n'a pas de fond, car le premier joueur gagne toujours, car il ne comprend qu'une portée. Dans le tableau 4x4, au contraire, il gagne toujours le deuxième joueur. Cela signifie que même si le premier joueur choisit la pièce qu'il souhaite, le second aura toujours la possibilité de placer la dernière pièce. En outre, dans tous les autres cas, le choix du deuxième joueur ne sera pas unique. Nous vous laissons invente ce cas spécial (le cas du joueur 2 a une seule chance).

Dans le tableau 5x5, le premier joueur gagne toujours si nous sélectionnons bien la première pièce. Quelle est cette pièce ?

A partir de maintenant, les possibilités sont multipliées en tables de plus grande dimension et il est difficile de réaliser une analyse détaillée. D'autre part, le tableau n'a pas de quadrilatère et on pourrait choisir d'autres tailles comme les rectangles 5x6, 3x20, 4x15, 5x12 ou 6x10. Dans le tableau 5x6 il y a un jeu approprié pour que le premier joueur gagne toujours. Qu'est-ce que c'est ?

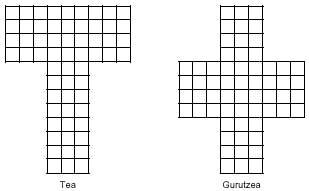
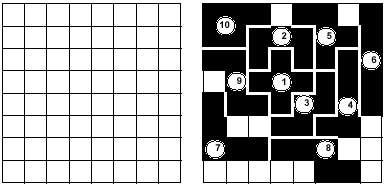
Vous pouvez faire la même chose pour jouer avec les hexamins. L'étude pour ce cas deviendrait inachevable, car il ya 35 pièces. En outre, il offre plus de possibilités quant au nombre de pièces. Voici le rectangle de 14x15 pour jouer avec les hexamins.